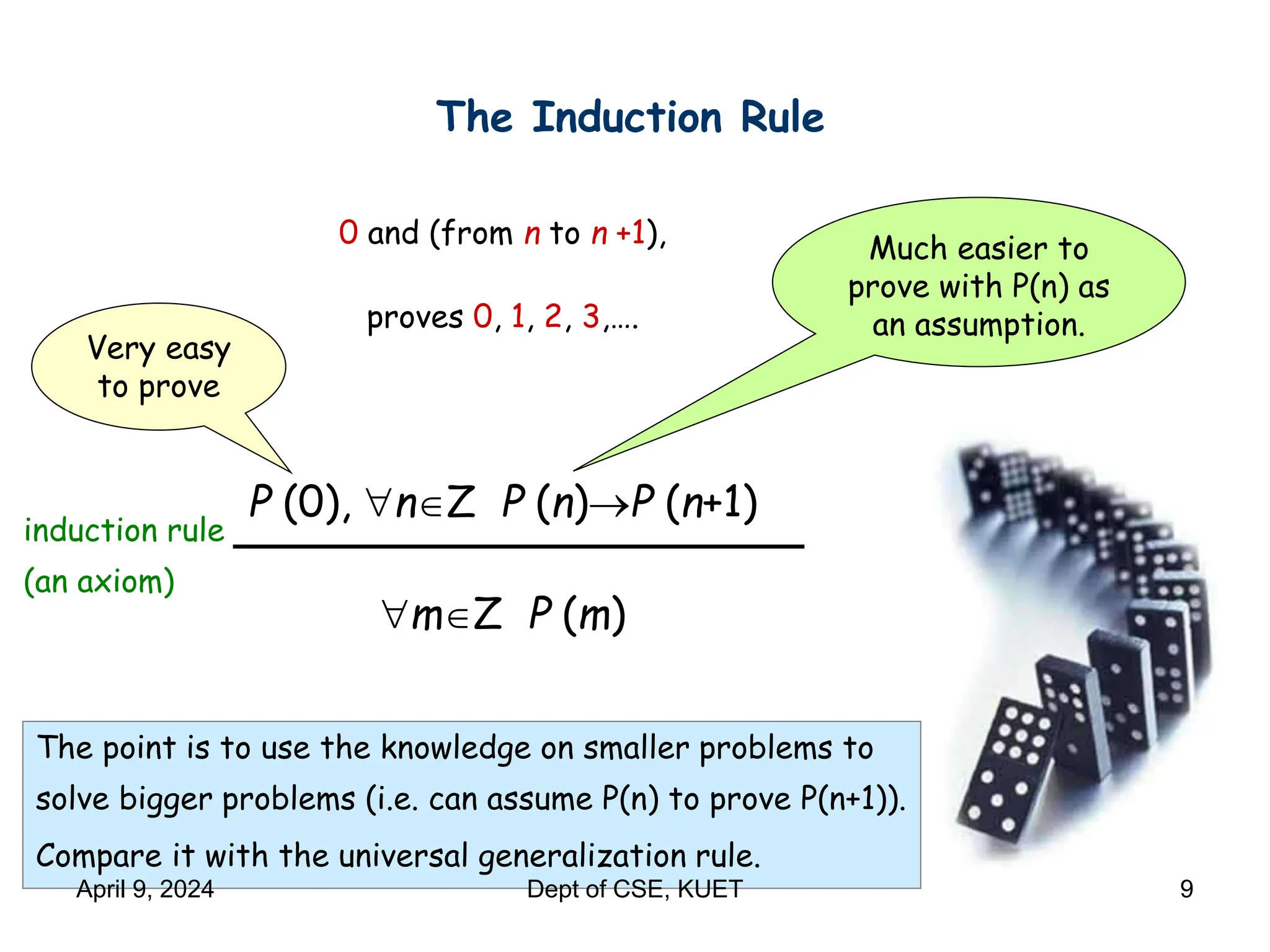
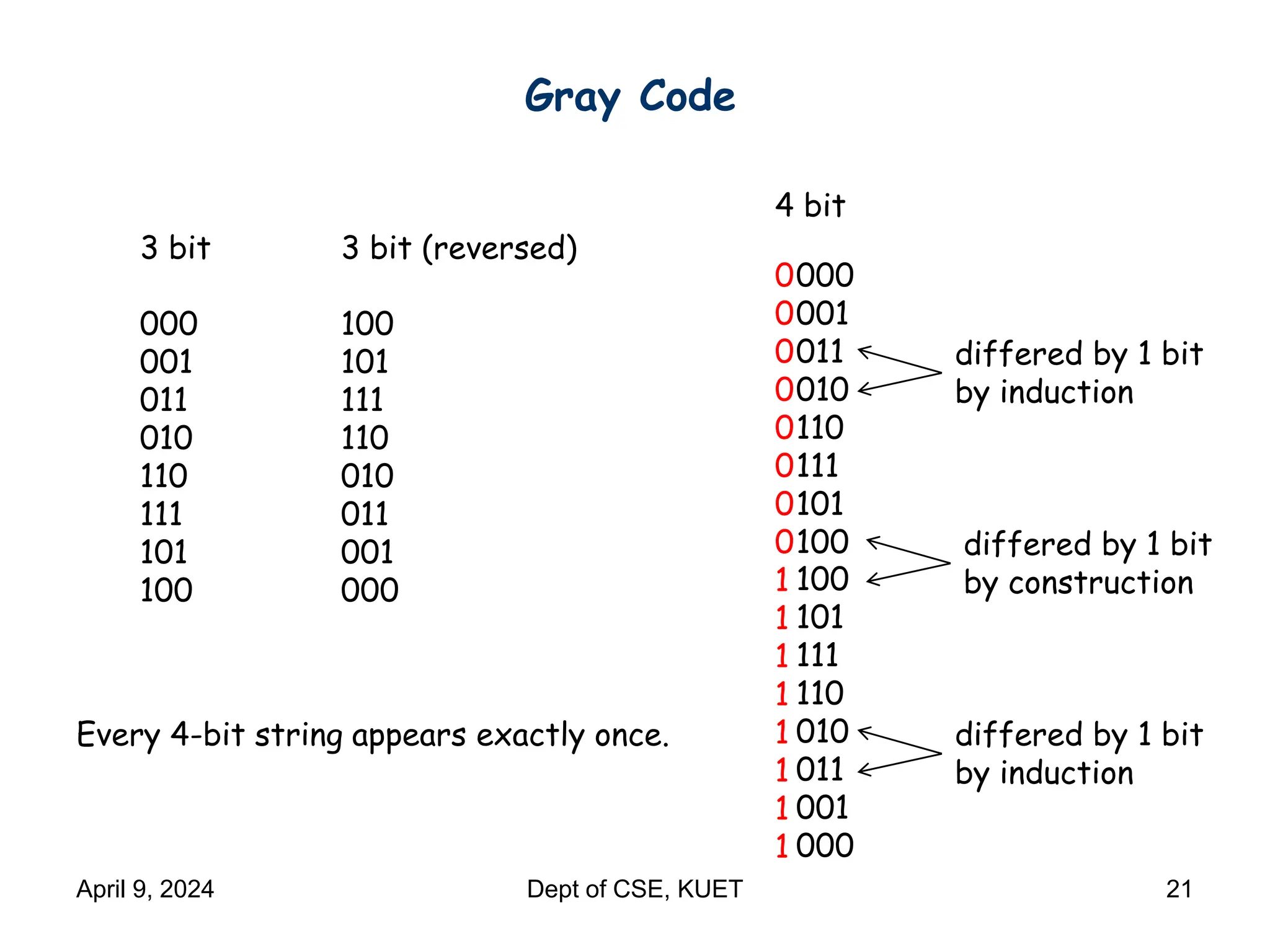
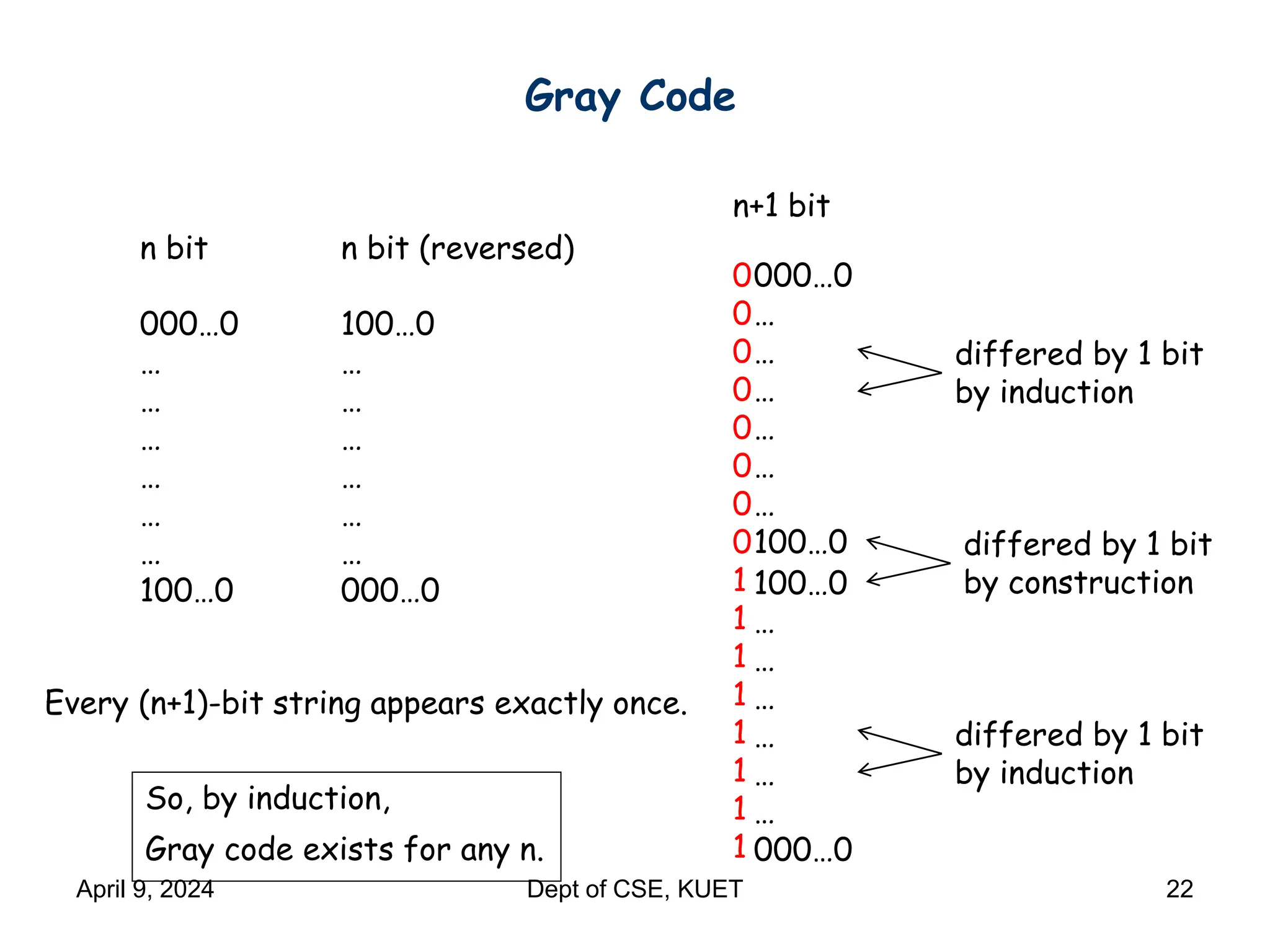
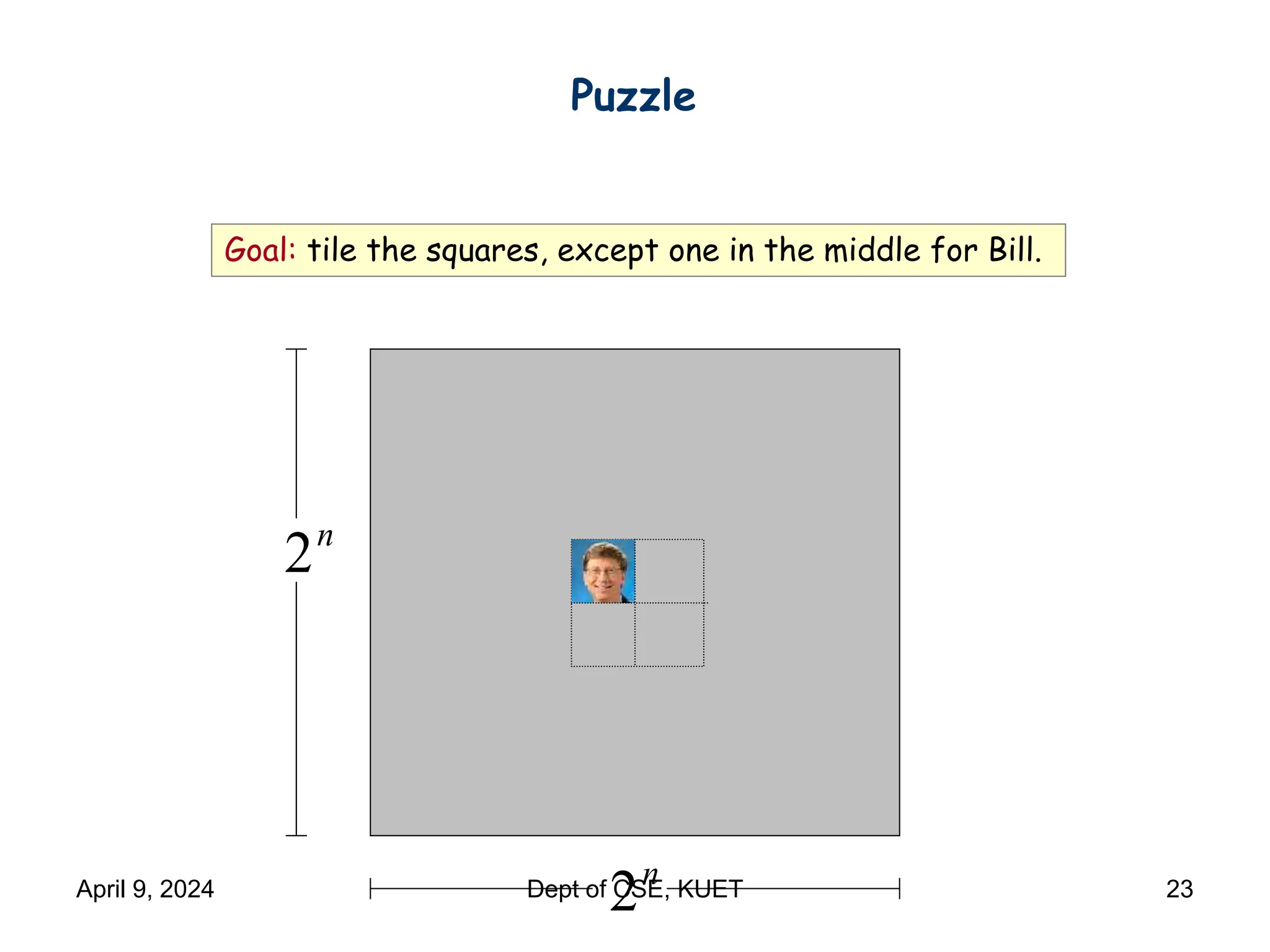
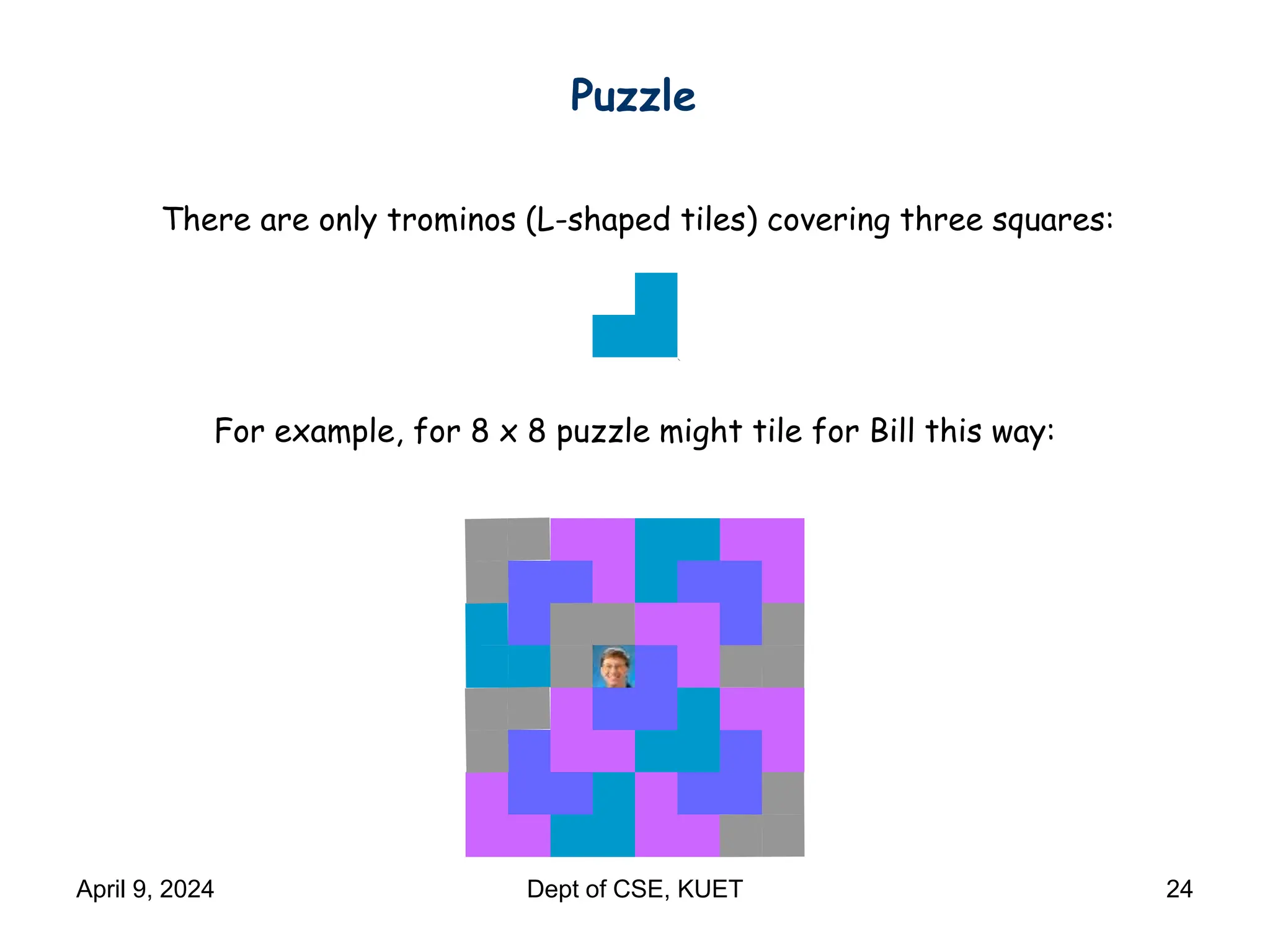
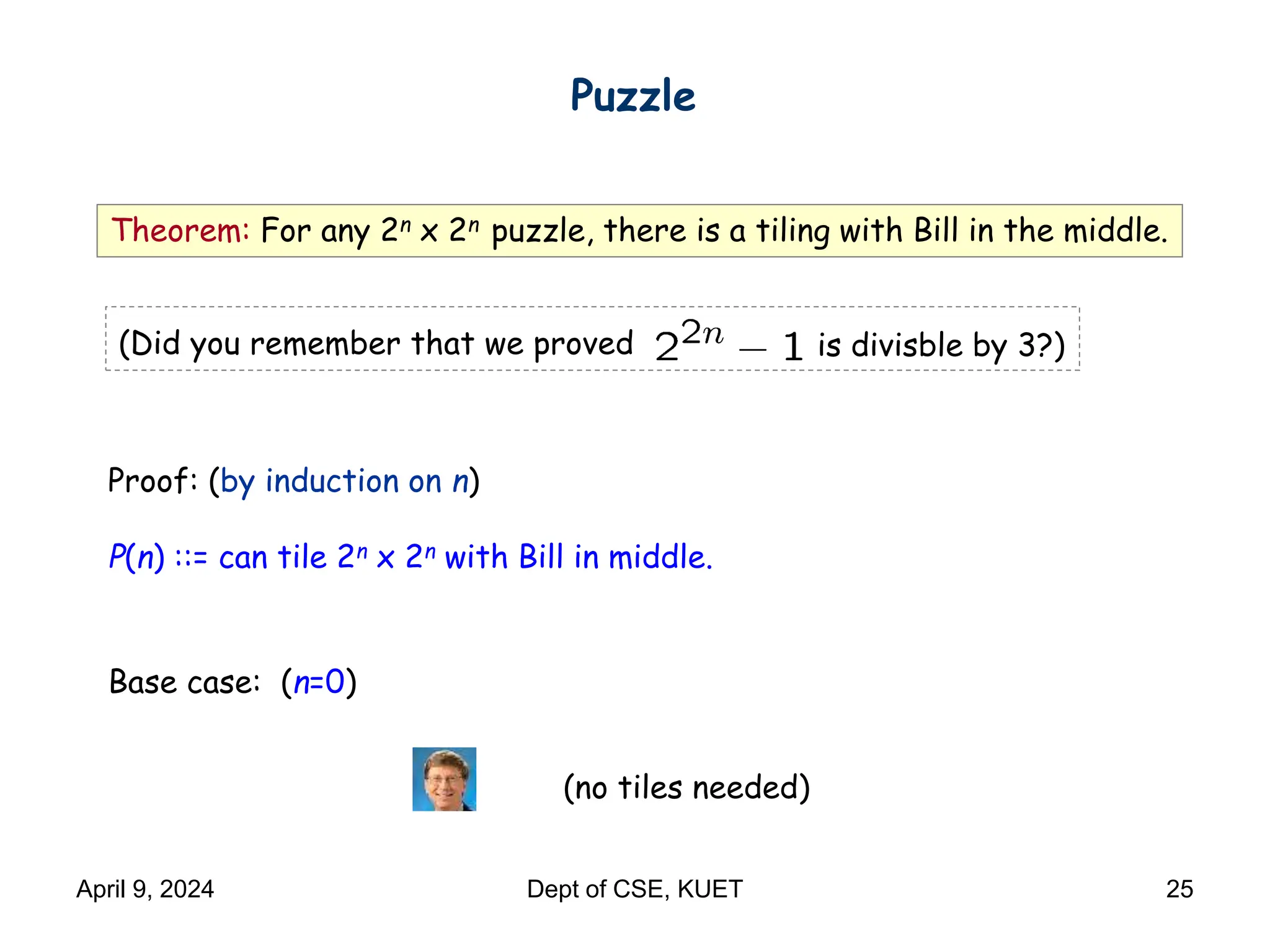
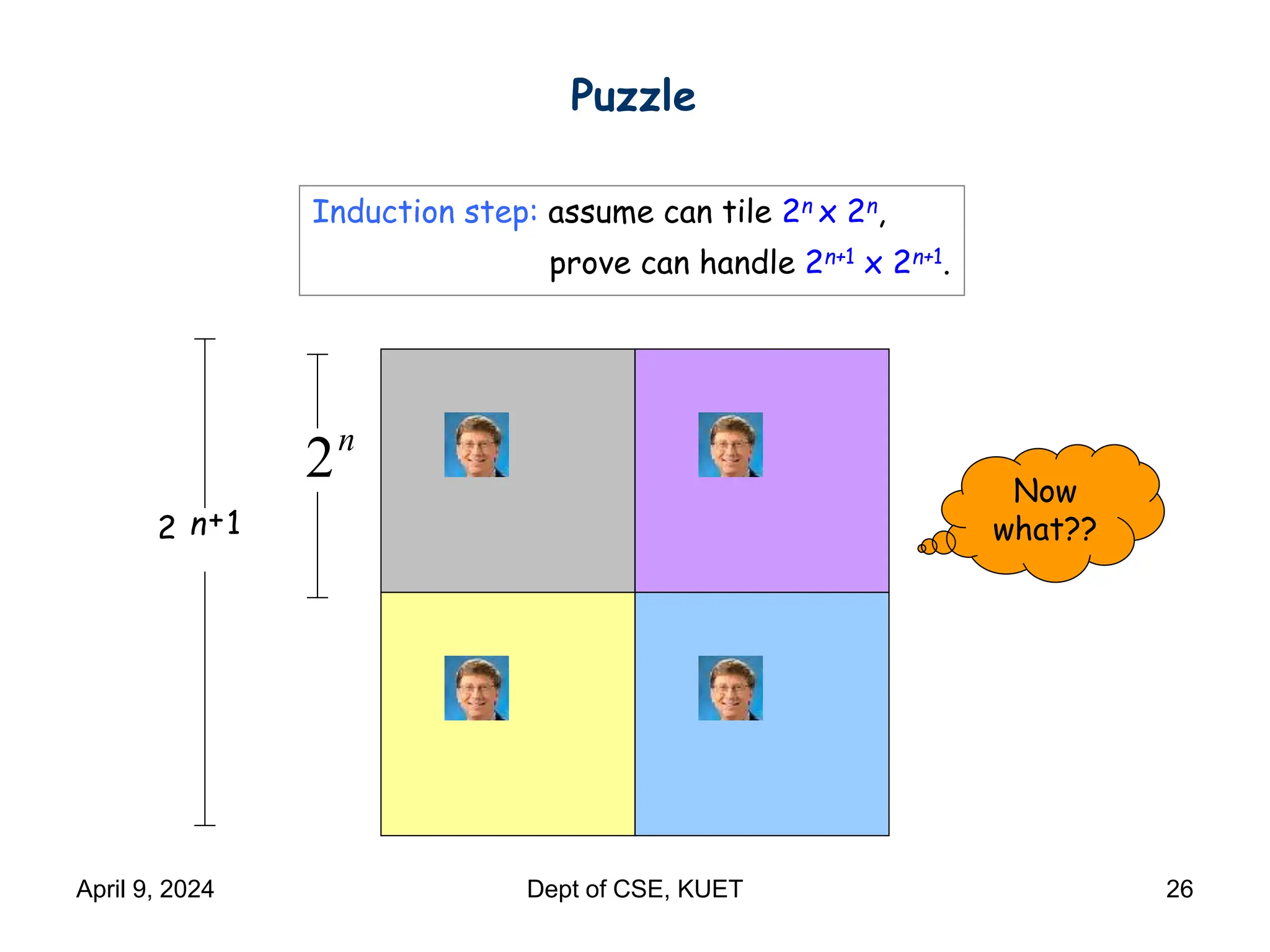
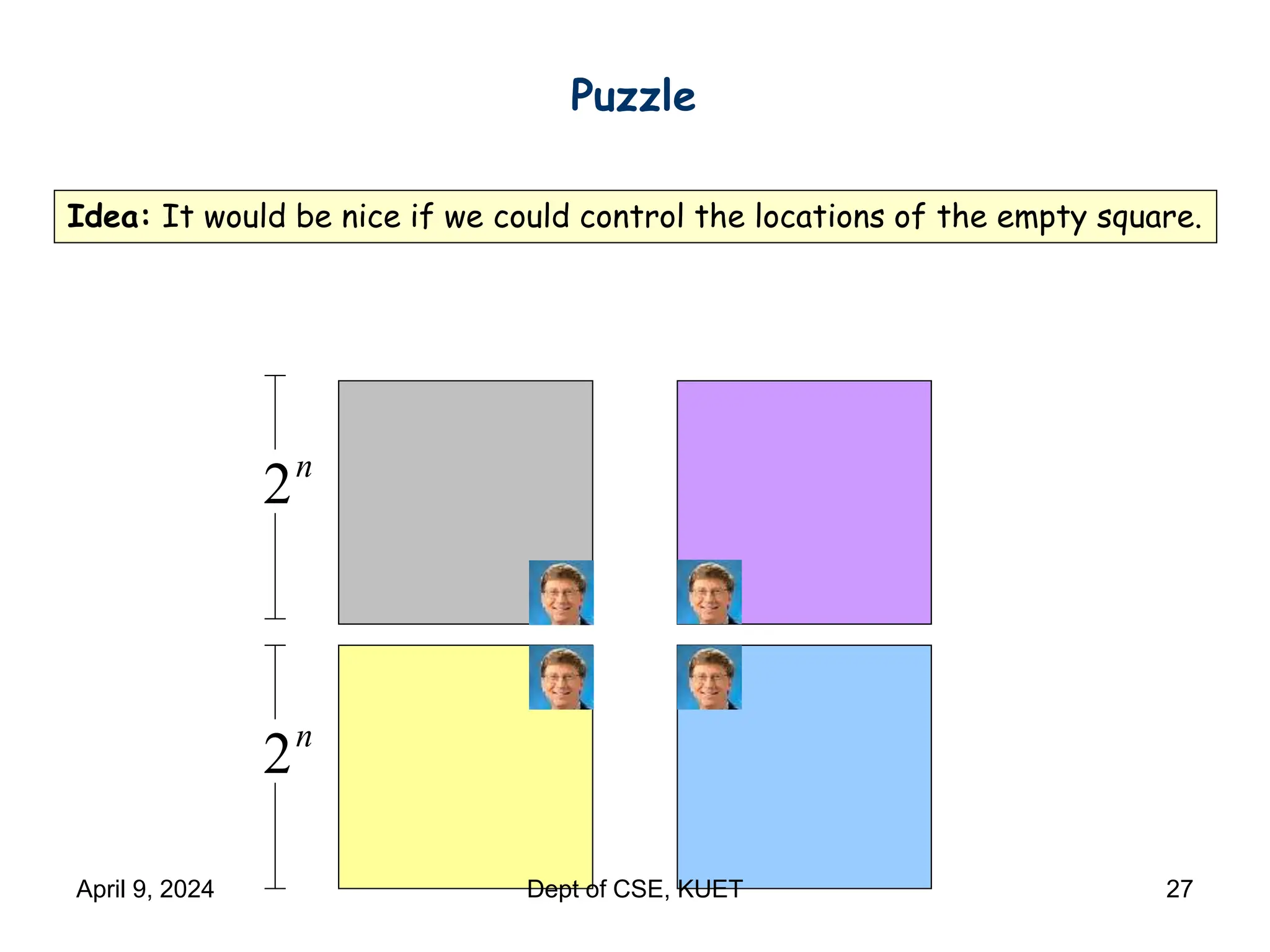
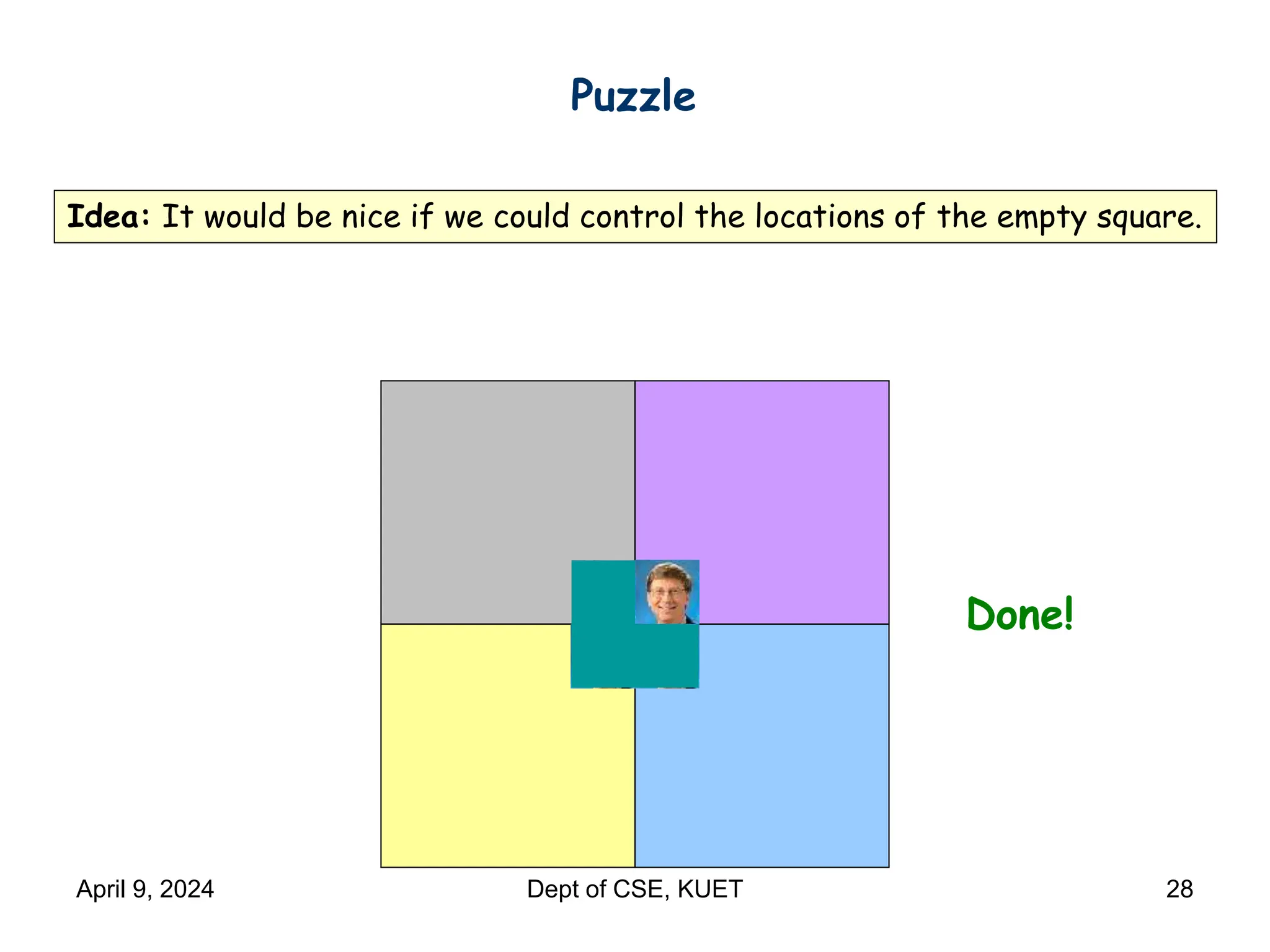
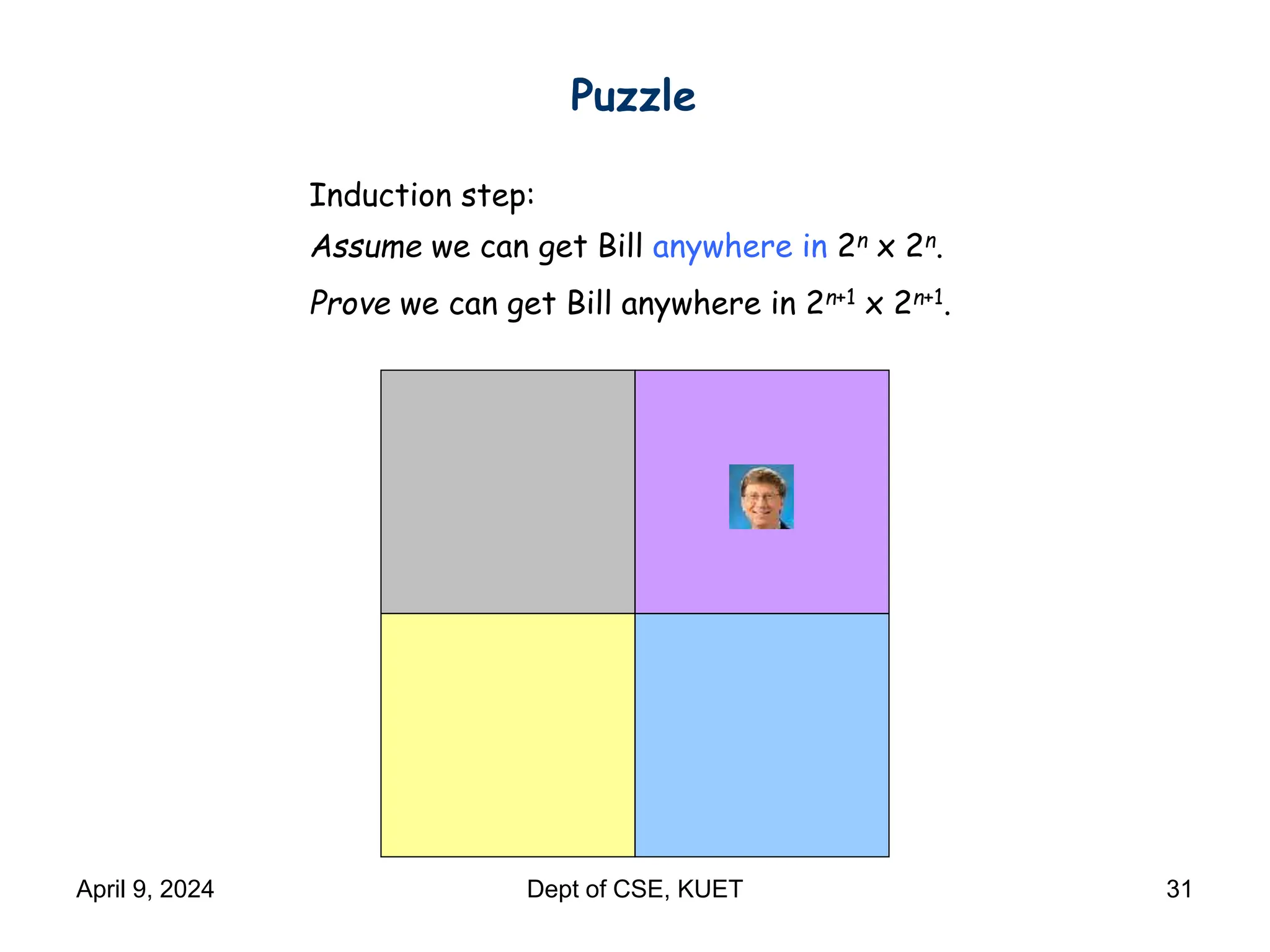
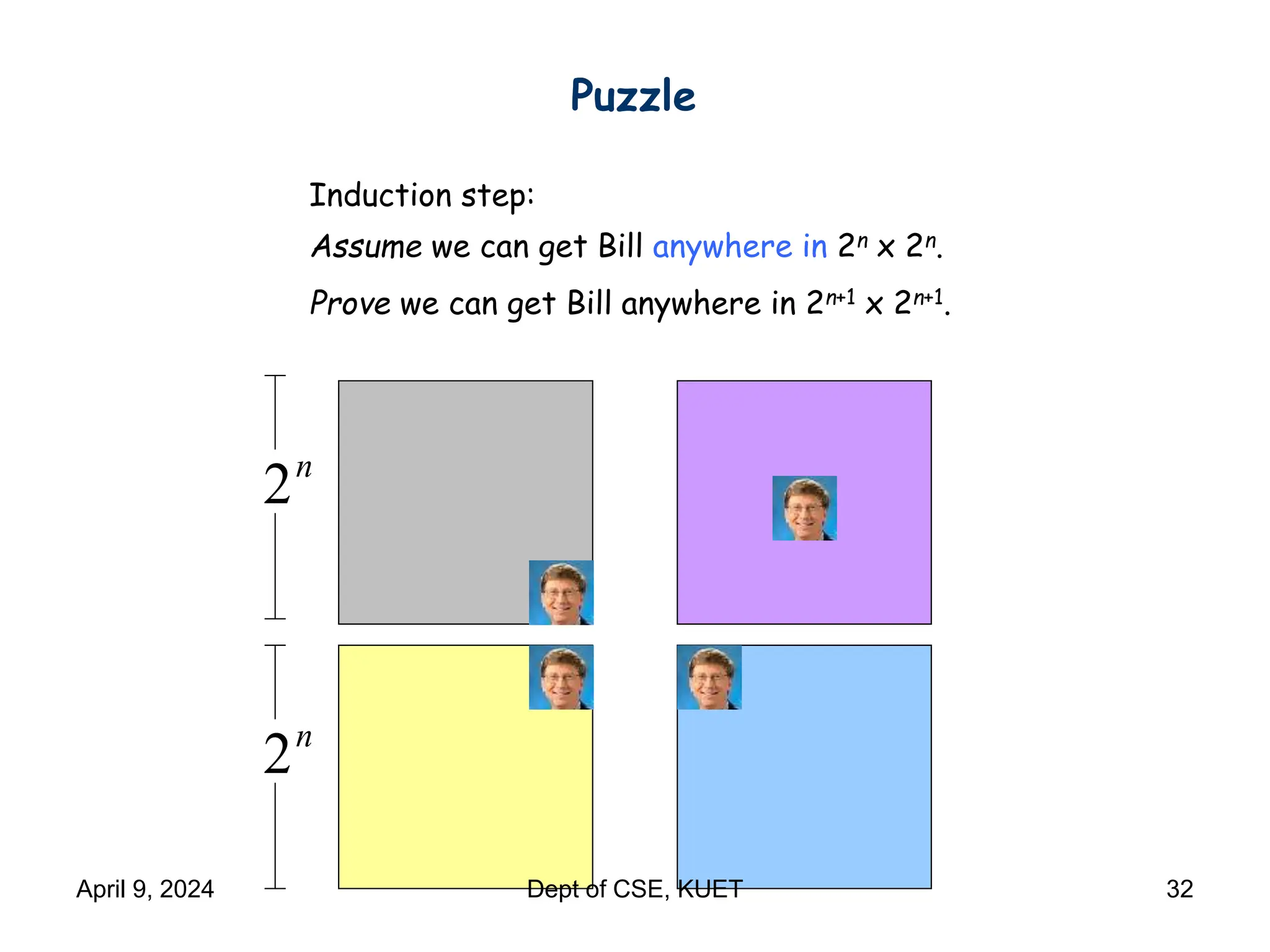
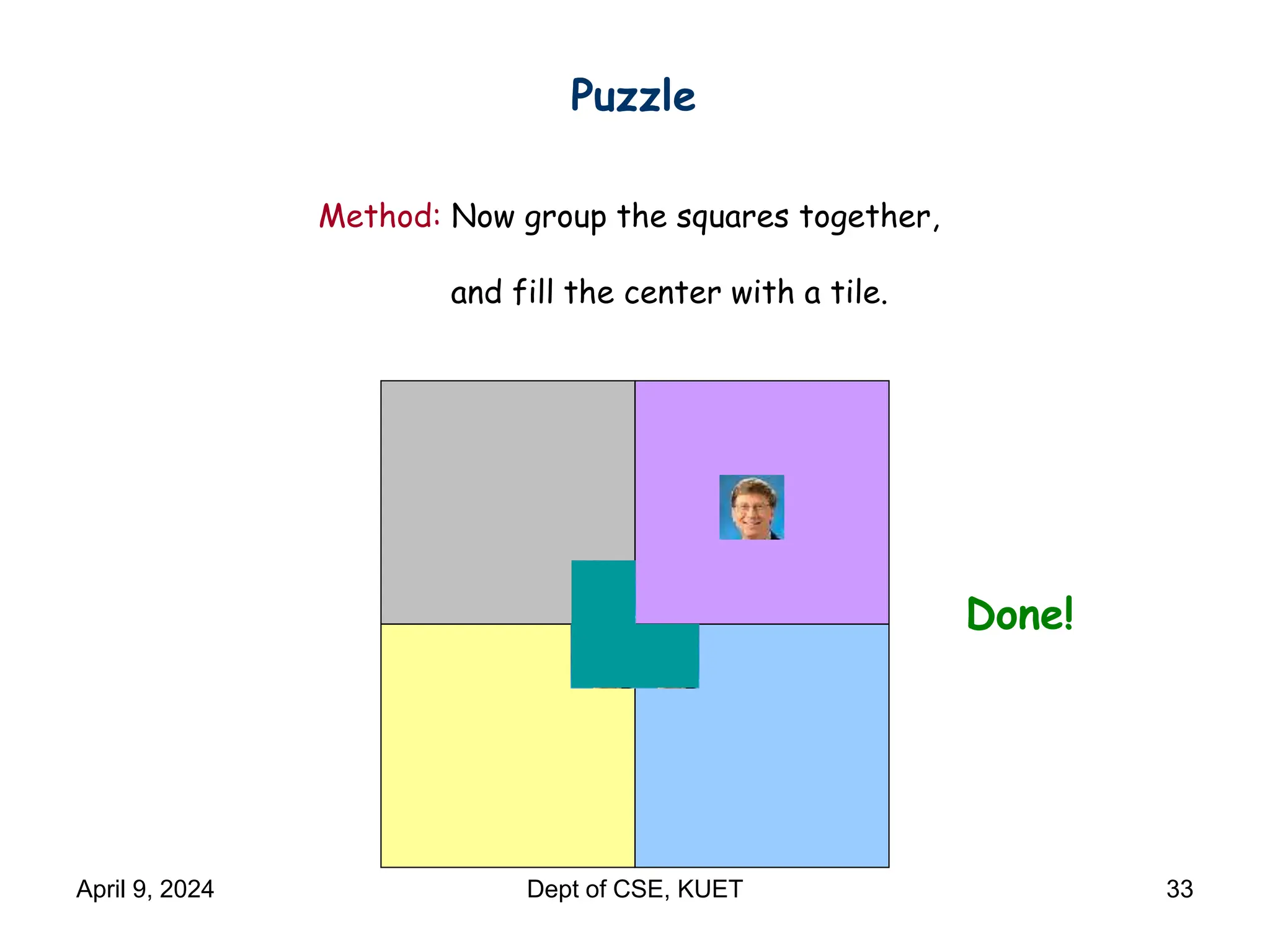
This document discusses mathematical induction. It begins by providing examples of using induction to prove statements about odd powers being odd and integers being divisible by prime numbers. It then discusses the basic idea and rules of mathematical induction. The document goes on to demonstrate induction proofs for equalities, inequalities, properties and the Cauchy-Schwarz inequality. It also discusses inductive constructions for Gray codes and Hadamard matrices. Finally, it mentions a paradox to demonstrate a limitation of induction.