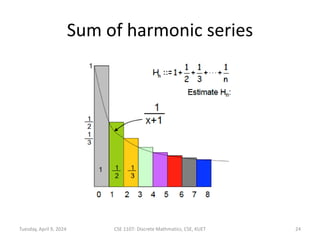
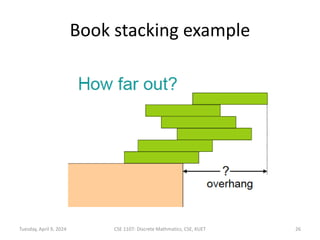
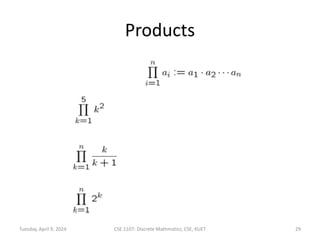
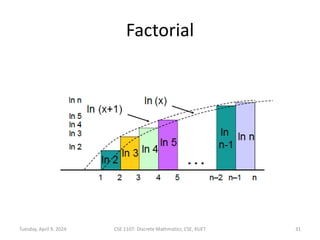
The document outlines lecture notes for a discrete mathematics course taught by Dr. M.M.A. Hashem at Khulna University of Engineering & Technology. It covers topics including sequences, series, summations, products, factorials, and countable sets. Examples of sequences discussed include arithmetic, geometric, and Fibonacci sequences. Formulas are provided for evaluating sums of arithmetic and geometric series.

1. CSE 1107: Discrete Mathematics
Sequence and Sums
M.M.A. Hashem, PhD
Professor
Dept. of Computer Science and Engineering
Khulna University of Engineering & Technology (KUET)
Khulna 9203, Bangladesh
Email: hashem@cse.kuet.ac.bd
Cell Phone: +880 1714 003949
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 1

2. Sequence
A sequence is an ordered list of elements.
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 2

3. Examples of Sequence
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 3

4. Examples of Sequence
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 4

5. Examples of Sequence
Not all sequences are arithmetic or geometric sequences.
An example is Fibonacci sequence
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 5

6. Fibonacci Sequence in Nature
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 6
13
8
5
3
2
1

7. Examples of Sequence
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 7

8. More on Fibonacci Sequence
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 8

9. Examples of Golden Ratio
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 9

10. Sequence Formula
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 10

11. Sequence Formula
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 11

12. Some useful sequences
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 12

13. Summation
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 13

14. Evaluating sequences
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 14

15. Arithmetic Series
Consider an arithmetic series a1, a2, a3, …, an. If the common
difference (ai+1 - a1) = d, then we can compute the kth term ak
as follows:
a2 = a1 + d
a3 = a2 + d = a1 +2 d
a4 = a3 + d = a1 + 3d
ak = a1 + (k-1).d
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 15

16. Evaluating sequences
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 16

17. Sum of arithmetic series
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 17

18. Solve this
Calculate 12 + 22 + 32+ 42 + … + n2
[Answer n.(n+1).(2n+1) / 6]
1 + 2 + 3 + … + n = ?
[Answer: n.(n+1) / 2] why?
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 18

19. Can you evaluate this?
Here is the trick. Note that
Does it help?
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 19

20. Double Summation
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 20

21. Sum of geometric series
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 21

22. Sum of infinite geometric series
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 22

23. Solve the following
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 23

24. Sum of harmonic series
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 24

25. Sum of harmonic series
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 25

26. Book stacking example
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 26

27. Book stacking example
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 27

28. Useful summation formulae
See page 157 of Rosen Volume 6
or
See page 166 of Rosen Volume 7
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 28

29. Products
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 29

30. Dealing with Products
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 30

31. Factorial
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 31

32. Factorial
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 32

33. Stirling’s formula
A few steps are omitted here
Here means that the ratio of the two sides approaches 1 as n approaches ∞
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 33

34. Countable sets
Cardinality measures the number of elements in a set.
DEF. Two sets A and B have the same cardinality, if and only if
there is a one-to-one correspondence from A to B.
Can we extend this to infinite sets?
DEF. A set that is either finite or has the same cardinality
as the set of positive integers is called a countable set.
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 34

35. Countable sets
Example. Show that the set of odd positive integers is countable.
f(n) = 2n-1 (n=1 means f(n) = 1, n=2 means f(n) = 3 and so on)
Thus f : Z+  {the set of of odd positive integers}.
So it is a countable set.
The cardinality of an infinite countable set is denoted by
(called aleph null)
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 35

36. Countable sets
Theorem. The set of rational numbers is countable.
Why? (See page 173 of the textbook)
Theorem. The set of real numbers is not countable.
Why? (See page 173-174 of the textbook).
Tuesday, April 9, 2024 CSE 1107: Discrete Mathmatics, CSE, KUET 36