Ktmt chuong 2

1
KIẾN TRÚC MÁY TÍNH
Chương 2.
BIỂU DIỄN DỮ LIỆU TRONG MÁY TÍNH

Phan Trung Kiên – ĐH Tây bắc 2
Chương 2.BIỂU DIỄN DỮ LIỆU TRONG MÁY TÍNH
 Thông tin trong máy tính
 Các hệ đếm và các loại mã dùng trong máy
tính
 Biểu diễn số nguyên
 Biểu diễn số thực bằng số dấu phẩy động
 Biểu diễn ký tự

2.1. Thông tin trong máy tính
 Phân loại thông tin
 Độ dài từ
 Thứ tự nhớ

Phân loại thông tin
 Dữ liệu nhân tạo: do con người quy ước
 Số nguyên
 Số thực
 Ký tự
 Dữ liệu tự nhiên: tồn tại khách quan với con
người
 Âm thanh
 Hình ảnh
 Nhiệt độ…

Độ dài từ dữ liệu
 Là số bit được sử dụng để mã hóa loại dữ
liệu tương ứng
 Trong thực tế thường là bội của 8 bit: 1, 8,
16, 32, 64 bit …

Thứ tự nhớ
 Thứ tự lưu trữ các byte của từ dữ liệu
 Bộ nhớ chính:
 Theo byte
 Độ dài từ dữ liệu
 Một hoặc nhiều byte
 Cần phải biết thứ tự lưu trữ các byte của
từ dữ liệu trong bộ nhớ chính

Lưu trữ kiểu đầu nhỏ (little-endian)
 Byte có ý nghĩa thấp hơn được lưu tữ trong bộ nhớ ở
địa chỉ nhỏ hơn
 Ví dụ: Từ dữ liệu 2 byte: 00001111 10101010
 Trong bộ nhớ
Byte1 Byte 0
00001111 10101010

Lưu trữ kiểu đầu to (big-endian)
 Byte có ý nghĩa thấp hơn được lưu tữ trong bộ nhớ ở
địa chỉ lớn hơn
 Ví dụ: Từ dữ liệu 2 byte: 00001111 10101010
 Trong bộ nhớ
Byte1 Byte 0
0000111110101010

Lưu trữ của các bộ xử lý điển hình
 Intel 80x86 và các Pentium: Little-endian
 Motorola 680x0 và các bộ xử lý RISC: Big-endian
 Power PC và Itanium: cả hai (bi-endian)

2.2. Các hệ đếm và các loại mã dùng trong
máy tính
 Hệ thập phân
 Hệ nhị phân
 Hệ bát phân
 Hệ thập lục phân

Hệ thập phân (Decimal System)
 Dùng 10 chữ số 0  9 để biểu diễn các số
 A = anan-1…a1a0.a-1a-2…a-m
 Giá trị của A
 = an*10n + an-1*10n-1 + … + a1*101 + a0*100 + a-1*10-1 + a-2*10-2 +
… + a-m*10-m
 Ví dụ: 123.456
 Mở rộng cho cơ số r bất kỳ
 = an*rn + an-1*rn-1 + … + a1*r1 + a0*r0 + a-1*r-1 + a-2*r-2 + … + a-m*r-
m
 Một chuỗi n chữ số của hệ đếm cơ số r sẽ biểu diễn
được rn chữ số.

Hệ nhị phân
 Sử dụng 2 chữ số 0 và 1 để biểu diễn các số
 Chữ số nhị phân gọi là bit (binary digit) là
đơn vị thông tin nhỏ nhất
 n bit biểu diễn được n giá trị khác nhau.
 00…000
 ……
 11…111

Dạng tổng quát của số nhị phân
 Có một số nhị phân A như sau:
 A = anan-1...a1a0.a-1...a-m
 Giá trị của A được tính như sau:
 A = an2n + an-12n-1 +...+ a020 + a-12-1 +...
+ a-m2-m

Ví dụ:

Chuyển đổi từ dạng thập phân sang nhị
phân
 Phương pháp 1: chia dần cho 2 rồi lấy phần
dư
 Phương pháp 2: phân tích thành tổng của
các số 2i  nhanh hơn

Phương pháp chia dần cho 2
 Ví dụ: chuyển đổi 105(10)
 105:2 = 52 dư 1
 52:2 = 26 dư 0
 26:2 = 13 dư 0
 13:2 = 6 dư 1
 6:2 = 3 dư 0
 3:2 = 1 dư 1
 1:2 = 0 dư 1
Kết quả: 105(10) = 1101001(2)

Phương pháp phân tích thành tổng của
các 2i
 Ví dụ 1: chuyển đổi 105(10)
 105 = 64 + 32 + 8 + 1 = 26 + 25 + 23 + 20
Kết quả: 105(10) = 1101001(2)

Chuyển số lẻ thập phân sang nhị phân
 Ví dụ 1: chuyển đổi 0.6875(10)
 0.6875 x 2 = 1.375 phần nguyên = 1
 0.375 x 2 = 0.75 phần nguyên = 0
 0.75 x 2 = 1.5 phần nguyên = 1
 0.5 x 2 = 1.0 phần nguyên = 1
Kết quả: 0.6875(10)=0.1011(2)

 0.81 x 2 = 1.62 phần nguyên = 1
 0.62 x 2 = 1.24 phần nguyên = 1
 0.24 x 2 = 0.48 phần nguyên = 0
 0.48 x 2 = 0.96 phần nguyên = 0
 0.96 x 2 = 1.92 phần nguyên = 1
 0.92 x 2 = 1.84 phần nguyên = 1
 0.84 x 2 = 1.68 phần nguyên = 1
Kết quả: 0.81(10) ~ 0.1100111(2)

 0.2 x 2 = 0.4 phần nguyên = 0
 0.4 x 2 = 0.8 phần nguyên = 0
 0.8 x 2 = 1.6 phần nguyên = 1
 0.6 x 2 = 1.2 phần nguyên = 1
 0.2 x 2 = 0.4 phần nguyên = 0
 0.4 x 2 = 0.8 phần nguyên = 0
 0.8 x 2 = 1.6 phần nguyên = 1
 0.6 x 2 = 1.2 phần nguyên = 1
Kết quả: 0.2(10) ~ 0.00110011(2)

Hệ bát phân (octal)
 Dùng 8 chữ số 0 7 để biểu diễn các số
 3 chữ số nhị phân ứng với 1 chữ số octal
 Ví dụ:
 Số nhị phân: 011 010 111
 Số octal: 3 2 7

Số thập lục phân (Hexa)
 Dùng 10 chữ số 09 và 6 chữ cái
A,B,C,D,E,F để biểu diễn các số.
 Dùng để viết gọn cho số nhị phân: cứ một
nhóm 4 bit sẽ được thay thế bằng 1 chữ
số Hexa

Quan hệ giữa số nhị phân và số Hexa
 Ví dụ chuyển đổi số nhị phân  số
Hexa:
 0000 00002 = 0016
 1011 00112 = B316
 0010 1101 1001 10102 = 2D9A16
 1111 1111 1111 11112 = FFFF16

2.3. Biểu diễn số nguyên
 Số nguyên không dấu
 Số nguyên có dấu
 Mã BCD

Số nguyên không dấu (Unsigned Integer)
 Biểu diễn số nguyên không dấu:
 Nguyên tắc tổng quát: Dùng n bit biểu diễn số
nguyên không dấu A: an-1an-2…..a2a1a0
 Giá trị của A được tính như sau:
 A = an2n + an-12n-1 +...+ a020
 Dải biểu diễn của A: từ 0 đến 2n-1

Ví dụ 1:
 Biểu diễn các số nguyên không dấu sau
đây bằng 8-bit: A=41 ; B=150
 Giải:
 A = 41 = 32 + 8 + 1 = 25 + 23 + 20
 41 = 0010 1001
 B = 150 = 128 + 16 + 4 + 2 = 27+24+22+21
 150 = 1001 0110

Ví dụ 2:
 Cho các số nguyên không dấu M, N được
biểu diễn bằng 8-bit như sau:
 M = 0001 0010
 N = 1011 1001
 Xác định giá trị của chúng?
 Giải:
 M = 0001 0010 = 24 + 21 = 16 + 2 = 18
 N = 1011 1001 = 27 + 25 + 24 + 23 + 20
 = 128 + 32 + 16 + 8 + 1 = 185

Trục số học số nguyên không dấu 8 bit
2550

Số nguyên có dấu
 Dấu và độ lớn
 Số bù một
 Số bù hai

Dấu và độ lớn
 Dùng bit MSB làm bit dấu
 0: số dương +
 1: số âm –
 Ví dụ: 27 và -27 (8 bit)
 +27 = 00011011
 -27 = 10011011

Ưu điểm – Nhược điểm
 Xét các số 3 bit:
 x: dạng nhị phân
 y: dạng thông thường

 Ưu:
 Trực quan
 Dễ dàng chuyển đổi dấu
 Nhược:
 Có hai biểu diễn của số 0
 Cộng trừ phải so sánh dấu
 Ít sử dụng

Trục số học
 Dải biểu diễn:
 -(2n-1 – 1) 2n-1 - 1

Số bù 1:
 Số bù 1 của A nhận được bằng cách đảo các
bit của A
 Ví dụ:
 0110 1001
 1001 0110

Ưu, nhược điểm
 Ưu:
 Trực quan
 Dễ dàng chuyển đổi dấu
 Nhược:
 Có hai biểu diễn của số 0
 Cộng trừ phải thực hiện thao tác đặc biệt
 Ít sử dụng

Trục số học
 -(2n-1 – 1) 2n-1 - 1

Số bù 2
 Số bù hai của A nhận được bằng cách lấy số
bù một của A cộng với 1
 Ví dụ: với n= 8 bit
 Giả sử có A = 0010 0101
 Số bù một của A = 1101 1010
 + 1
 Số bù hai của A = 1101 1011
 Vì A + (Số bù hai của A) = 0  dùng số bù
hai để biểu diễn cho số âm

Số bù 2
 Nguyên tắc tổng quát: Dùng n bit biểu diễn số
nguyên có dấu A:
 an-1an-2…a1a0
 Với A là số dương: bit an-1 = 0, các bit còn lại
biểu diễn độ lớn như số không dấu
 Với A là số âm: được biểu diễn bằng số bù hai
của số dương tương ứng, vì vậy bit an-1 = 1

Số bù 2

Số bù 2
 Ví dụ 1. Biểu diễn các số nguyên có dấu sau đây
bằng 8 bit:
 A = +58 ; B = -80
 Giải:
 A = +58 = 0011 1010
 B = -80
 Ta có: +80 = 0101 0000
 Số bù một = 1010 1111
 + 1
 Số bù hai = 1011 0000
 Vậy: B = -80 = 1011 0000

Số bù 2
 Ví dụ 2: Hãy xác định giá trị của các số
nguyên có dấu được biểu diễn dưới đây:
 P = 0110 0010
 Q = 1101 1011
 Giải:
 P = 0110 0010 = 64 + 32 + 2 = +98
 Q = 1101 1011 = -128+64+16+8+2+1 = -37

Ưu, nhược điểm
 Ưu:
 Cộng trừ dễ dàng
 Có 1 giá trị 0
 Nhược:
 Không đối xứng

Trục số học
 -2n-1 2n-1 - 1

Đổi số n bit sang m bit (m>n)
 Đổi số dương
 Thêm các bit 0 vào đầu
 Đổi số âm
 Thêm các bit 1 vào đầu

Biểu diễn số nguyên theo mã BCD
 BCD - Binary Coded Decimal Code
 Dùng 4 bit để mã hoá cho các chữ số thập phân
từ 0 đến 9
 0  0000 1  0001 2  0010
 3  0011 4  0100 5  0101
 6  0110 7  0111 8  1000
 9  1001
 Có 6 tổ hợp không sử dụng:
1010, 1011, 1100, 1101, 1110, 1111

Ví dụ số BCD
 35
  0011 0101BCD
 61
  0110 0001BCD
 1087
  0001 0000 1000 0111BCD
 9640
  1001 0110 0100 0000BCD

Các kiểu lưu trữ số BCD

Thực hiện phép toán số học với số nguyên
 Phép cộng
 Phép trừ
 Phép nhân
 Phép chia

Phép cộng
 Số nguyên không dấu
 Dùng bộ cộng n bit
 Nguyên tắc:
 Khi cộng hai số nguyên không dấu n-bit, kết quả
nhận được là n-bit:
 Nếu không có nhớ ra khỏi bit cao nhất thì kết quả
nhận được luôn luôn đúng (Cout = 0).
 Nếu có nhớ ra khỏi bit cao nhất thì kết quả nhận
được là sai,  có tràn nhớ ra ngoài (Cout = 1).
 Tràn nhớ ra ngoài (Carry Out) xảy ra khi tổng >2n-1

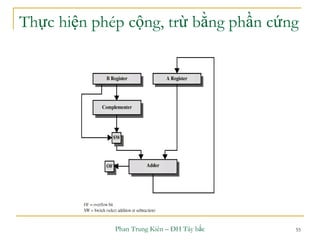
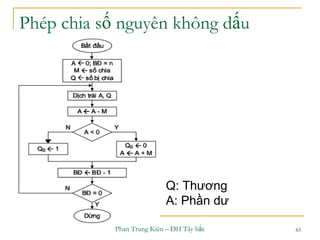
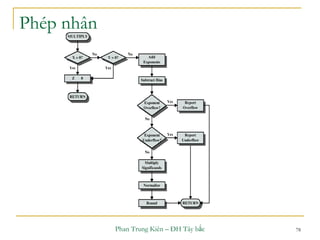
Phép cộng số có dấu
 Khi cộng 2 số nguyên có dấu n-bit không quan tâm
đến bit Cout và kết quả nhận được là n-bit:
 Cộng 2 số khác dấu: kết quả luôn luôn đúng.
 Cộng 2 số cùng dấu:
 Nếu dấu kết quả cùng dấu với các số hạng thì kết quả là
đúng.
 Nếu kết quả có dấu ngược lại, khi đó có tràn xảy ra
(Overflow) và kết quả là sai.
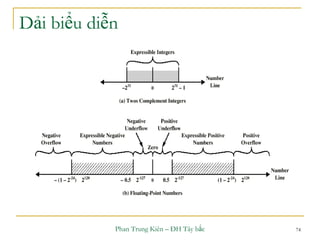
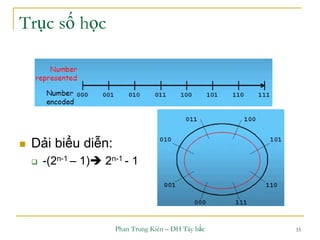
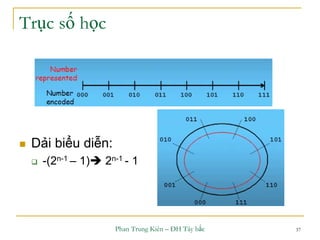
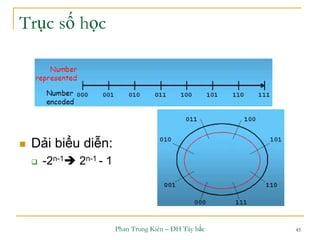
 Tràn xảy ra khi tổng nằm ngoài dải biểu diễn
[-(2n-1),+(2n-1-1)]

Phép trừ
 Phép đảo dấu
 Lấy bù 2
 Trường hợp đặc biệt
 Số 0
 Số 11…111

Phép trừ
 Phép trừ 2 số nguyên: X – Y = X + (-Y)
 Nguyên tắc: Lấy bù hai của Y để được –Y,
rồi cộng với X

Thực hiện phép cộng, trừ bằng phần cứng

Phép nhân số nguyên không dấu
 1011 Số bị nhân (11)
 x 1101 Số nhân (13)
 1011 Tích riêng phần
 0000
 1011
 1011
 10001111 Tích (143)

Phép nhân số nguyên không dấu
 Nhận xét:
 Nếu bit của số nhân là 1:
tích riêng phần là số bị nhân
 Nếu bit của số nhân là 0:
tích riêng phần là 0
 Tích riêng phần sau dịch trái 1 bit so với tích
riêng phần trước
 Tích là tổng các tích riêng phần và có số bit
gấp đôi số bit của các thừa số.

Sơ đồ thực hiện:

Lưu đồ thuật toán
Các thanh ghi M, Q, A: n bit
C: 1 bit
2 thừa số là n-bit
 tích là số 2n-bit được chứa
trong cặp thanh ghi A, Q

Ví dụ: thực hiện 11*13 (với số 4 bit)
Q0

Nhân số nguyên có dấu
 Phương pháp 1:
 Chuyển đổi các thừa số thành số dương
 Nhân 2 số dương như số nguyên không dấu
 Hiệu chỉnh dấu của kết quả:
 Nếu 2 thừa số khác dấu  đảo dấu kết quả bằng
 Nếu 2 thừa số cùng dấu  không cần hiệu chỉnh cách
lấy bù 2.

Nhân số nguyên có dấu
 Phương pháp 2:
 Dùng giải thuật Booth

Phép chia số nguyên không dấu
Q: Thương
A: Phần dư

Chia số nguyên có dấu
Cách 1:
 Sử dụng thuật giải chia số nguyên không dấu
 Đổi số bị chia và số chia  dương
 Chia như số nguyên không dấu  thương
và phần dư (đều là số dương)
 Hiệu chỉnh dấu:
 (+) : (+)  không hiệu chỉnh dấu kết quả
 (+) : (-)  đảo dấu thương
 (-) : (+)  đảo dấu thương và phần dư
 (-) : (-)  đảo dấu phần dư

Chia số nguyên có dấu
Cách 2: Sử dụng thuật toán sau:
 B1: Nạp số chia vào M, số bị chia vào A,Q
 B2: Dịch trái A,Q 1 bit
 B3:
 Nếu A và M cùng dấu thì A = A - M
 Ngược lại: A = A + M
 B4:
 Nếu dấu của A trước và sau B3 là như nhau hoặc (A = Q = 0) thì
Q0 = 1
 Ngược lại Q0 = 0, khôi phục lại giá trị của A trước bước 3
 B5: Lặp B2  B4 n lần
 B6:
 Phần dư nằm trong A
 Nếu dấu của số chia và số bị chia giống nhau: thương là Q
 Ngược lại: thương là bù 2của Q

2.4. Biểu diễn số thực bằng số dấu chấm
động
 Khái niệm
 Chuẩn IEEE 754/85
 Các phép toán

Khía niệm số dấu chấm động
(FPN – Floating Point Number)
 Tổng quát: một số thực X được biểu diễn
theo kiểu số dấu chấm động như sau:
 X = M * RE
 M là phần định trị (Mantissa),
 R là cơ số (Radix),
 E là phần mũ (Exponent).

Chuẩn IEEE 754/85
 Cơ số R = 2
 Các dạng:
 Dạng 32-bit (chính xác đơn)
 Dạng 64-bit (chính xác kép)
 Dạng 80-bit (chính xác kép mở rộng)

Dạng 32 bit
•S là bit dấu:
•S = 0  Số dương
•S = 1  Số âm
•e (8 bit) là mã excess-127 của phần mũ E:
•e = E + 127  E = e – 127
•giá trị 127 được gọi là độ lệch (bias)
•m (23 bit) là phần lẻ của phần định trị M:
•M = 1.m
•Công thức xác định giá trị của số thực:
•X = (-1)S*1.m*2e-127

Dạng 64 bit
•S là bit dấu:
•S = 1  Số âm
•e = E + 1023  E = e – 1023
•M = 1.m
•X = (-1)S*1.m*2e-1023

Dạng 80 bit
•S là bit dấu:
•S = 1  Số âm
•e = E + 16383  E = e – 16383
•M = 1.m
•X = (-1)S*1.m*2e-16383

Ví dụ
20 = 101002, 127 = 011111112, 147 = 100100112, 107 = 011010112
0.638125 = 1/2 + 1/8 +1/128 = .10100012

Câu hỏi
 Tại sao lại biểu diễn m mà không biểu diễn M?
 Tại sao lại biểu diễn e mà không biểu diễn E?

Dải biểu diễn

Câu hỏi
 Khi tăng số bit m?
 Khi tăng số bit e?
 Dạng 32 bit biểu diễn được bao nhiêu số?

Các quy ước đặc biệt
 Các bit của e bằng 0, các bit của m bằng 0, thì X=  0
 Các bit của e bằng 1, các bit của m bằng 0, thì X= ± 
 Các bit của e bằng 1, còn m có ít nhất 1 bit bằng 1, thì
nó không biểu diễn cho số nào cả (NaN – not a
number)
 x000 0000 0000 0000 0000 0000 0000 0000
 X= ± 0
 x111 1111 1000 0000 0000 0000 0000 0000 
X= ± 
 x111 1111 1000 0000 0000 0000 0000 0001 
X= NaN

Phép +, -

Phép nhân

Phép chia

Biểu diễn ký tự
 Bộ mã ASCII (American Standard Code for
 Information Interchange)
 Bộ mã Unicode

Bộ mã ASCII
 Do ANSI (American National Standard
Institute) thiết kế
 Bộ mã 8 bit  có thể mã hóa được 28 =256
ký tự, có mã từ: 0016  FF16 , trong đó:
 128 ký tự chuẩn, có mã từ 0016  7F16
 128 ký tự mở rộng, có mã từ 8016  FF16

Bộ mã ASCII

Các ký tự mở rộng: có mã 8016 ¸ FF16
 Các ký tự mở rộng được định nghĩa bởi:
 nhà chế tạo máy tính
 người phát triển phần mềm
 Ví dụ:
 Bộ mã ký tự mở rộng của IBM: IBM-PC.
 Bộ mã ký tự mở rộng của Apple: Macintosh.
 Có thể thay đổi các ký tự mở rộng để mã hóa
cho các ký tự riêng của tiếng Việt, ví dụ như bộ
mã TCVN3.

Bộ mã hợp nhất Unicode
 Do các hãng máy tính hàng đầu thiết kế
 Bộ mã 16-bit
 Bộ mã đa ngôn ngữ
 Có hỗ trợ các ký tự tiếng Việt

Ktmt chuong 2

More Related Content

What's hot

Viewers also liked

Similar to Ktmt chuong 2

Ktmt chuong 2