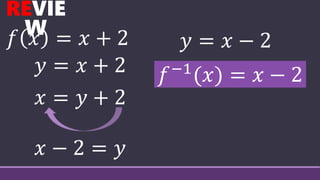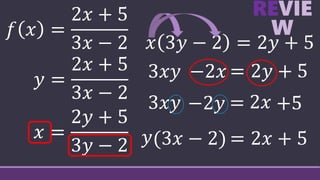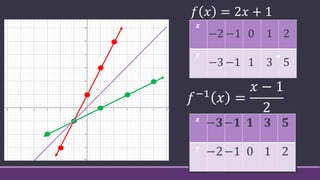
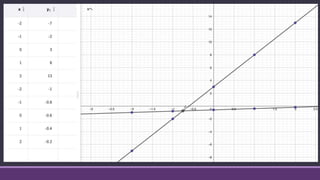
1) The document defines the inverse of a function as another function that undoes the original function. 2) It provides examples of finding the inverse of different functions by setting them equal to each other and solving for the input variable in terms of the output variable. 3) The inverse of a function can be represented using a table of values that relates the outputs of the original function to the inputs of the inverse function and vice versa.

1. Inverse Function
defined with table of
values and graph.
BNHS-SHS (GENERAL MATHEMATICS)

2. Find the inverse of the given function.
𝑓 𝑥 = 𝑥 + 2

3. REVIE
W
𝑓 𝑥 = 𝑥 + 2
𝑦 = 𝑥 + 2
𝑥 = 𝑦 + 2
𝑥 − 2 = 𝑦
𝑦 = 𝑥 − 2
𝑓−1
(𝑥) = 𝑥 − 2

4. Find the inverse of the given function.
𝑓 𝑥 = 12𝑥 − 1

5. REVIE
W
𝑓 𝑥 = 12𝑥 − 1
𝑦 = 12𝑥 − 1
𝑥 = 12𝑦 − 1
𝑥 + 1 = 12𝑦
12𝑦 = 𝑥 + 1
12𝑦
12
=
𝑥 + 1
12
𝑓−1
(𝑥) =
𝑥 + 1
12

6. Find the inverse of the given function.
𝑓 𝑥 =
2𝑥 + 3
3𝑥 − 2

7. REVIE
W
𝑓 𝑥 =
2𝑥 + 5
3𝑥 − 2
𝑦 =
2𝑥 + 5
3𝑥 − 2
𝑥 =
2𝑦 + 5
3𝑦 − 2
𝑥 3𝑦 − 2 = 2𝑦 + 5
3𝑥𝑦 −2𝑥 = 2𝑦 + 5
3𝑥𝑦 =
−2𝑦 2𝑥 +5
𝑦(3𝑥 − 2) = 2𝑥 + 5

8. REVIE
𝑦 3𝑥 − 2 = 2𝑥 + 5
𝑦 3𝑥 − 2
3𝑥 − 2
=
2𝑥 + 5
3𝑥 − 2
𝑓−1
(𝑥) =
2𝑥 + 5
3𝑥 − 2

9. Table of Values of Inverse
Function
𝑓 𝑥 = 2𝑥 + 1
𝒙
f(𝑥)
−2 −1 0 1 2
−3 −1 1 3 5

10. Table of Values of Inverse
Function
𝑓 𝑥 = 2𝑥 + 1
𝑦 = 2𝑥 + 1
𝑥 − 1 = 2𝑦
𝑥 = 2𝑦 + 1
2𝑦 = 𝑥 − 1
2𝑦
2
=
𝑥 − 1
2
𝑓−1
(𝑥) =
𝑥 − 1
2

11. 𝑓 𝑥 = 2𝑥 + 1
𝒙
𝑦
−2 −1 0 1 2
−3 −1 1 3 5
𝑓−1
𝑥 =
𝑥 − 1
2
𝒙
−𝟑−𝟏 𝟏 𝟑 𝟓
𝑦
−2−1 0 1 2

12. 𝑓 𝑥 = 2𝑥 + 1
−2 −1 0 1 2
−3 −1 1 3 5 𝑓−1 𝑥 =
𝑥 − 1
2

13. Group Activity

14. 𝑓 𝑥 = 3𝑥 − 4 𝑓−1 𝑥 =
𝑥 + 4
3

15. 𝑓 𝑥 = 3𝑥 − 4 𝑓−1 𝑥 =
𝑥 + 4
3

16. 𝑓 𝑥 = 5𝑥 + 3 𝑓−1
𝑥 =
𝑥 − 3
5

17. 𝑓 𝑥 = 3𝑥 − 4 𝑓−1 𝑥 =
𝑥 + 4
3