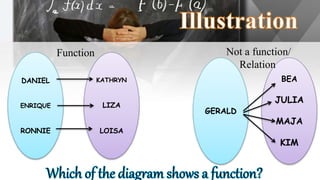
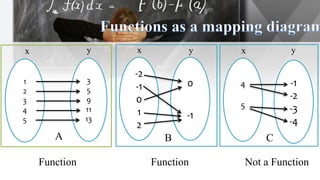
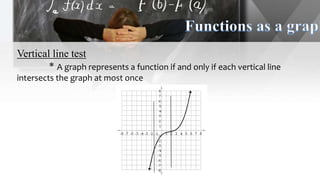
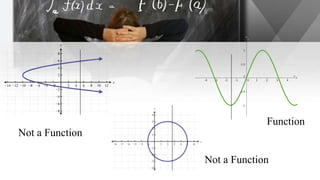
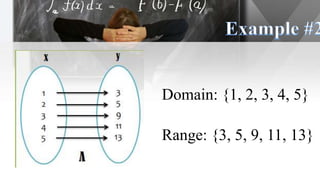
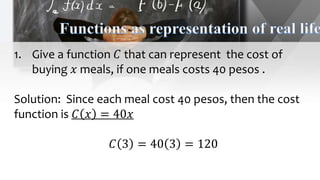The document discusses functions, including their definition, domains, and ranges, and how to represent real-life situations with functions, such as piecewise functions. It provides examples of identifying functions from sets of ordered pairs and illustrates function rules with practical scenarios like cost estimation. Additionally, it explains criteria for functions, including the vertical line test to determine if a graph represents a function.