Download to read offline
Introduction-to-Divide-and-Conquer_(1).pptx
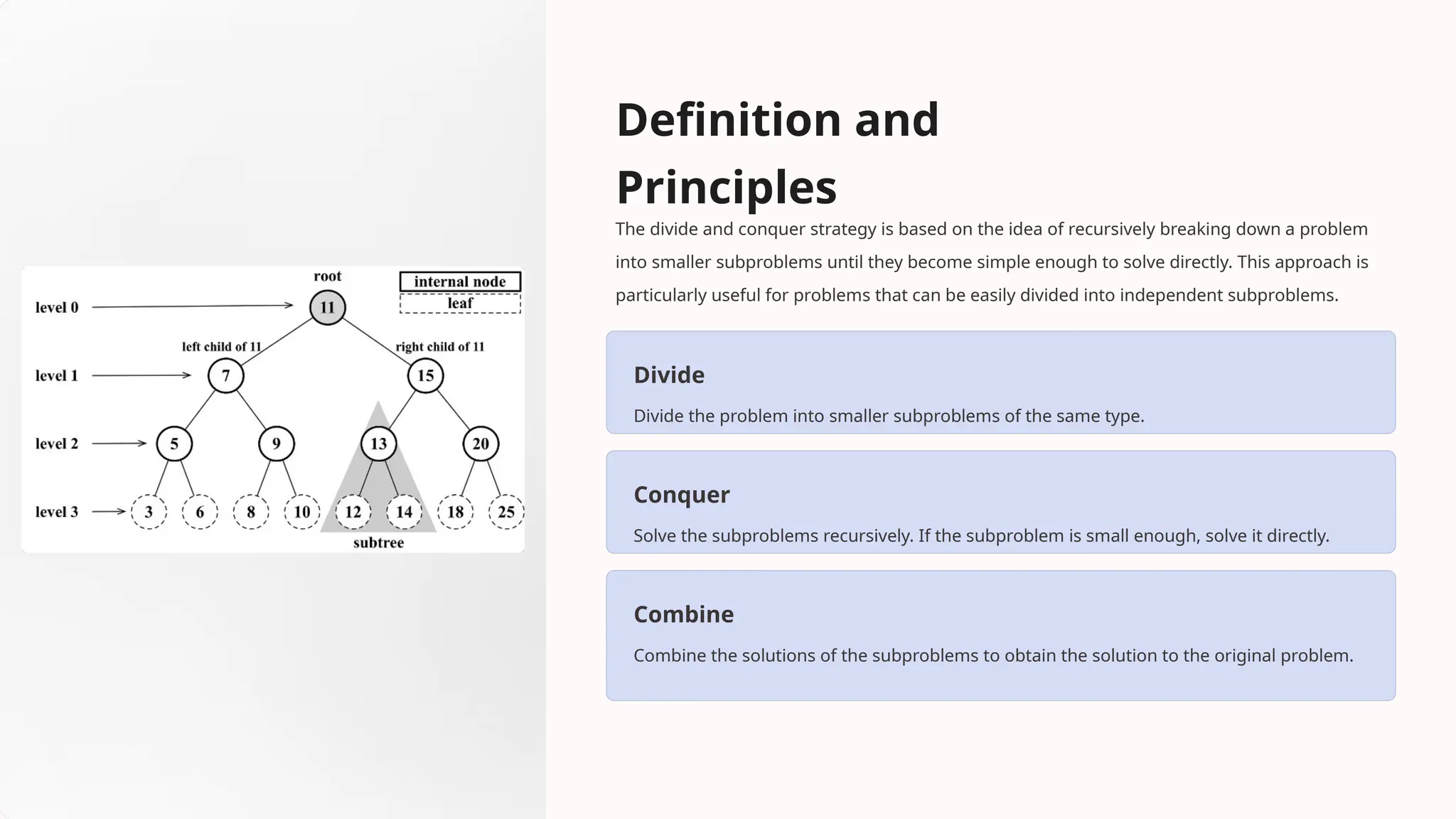
- 1. Introduction to Divide and Conquer Divideand conquer is a powerful problem-solving technique used in computer science and mathematics. It involves breaking down a complex problem into smaller, more manageable subproblems that are easier to solve. by Prithvi Singh
- 2. Definition and Principles The divideand conquer strategy is based on the idea of recursively breaking down a problem into smaller subproblems until they become simple enough to solve directly. This approach is particularly useful for problems that can be easily divided into independent subproblems. Divide Divide the problem into smaller subproblems of the same type. Conquer Solve the subproblems recursively. If the subproblem is small enough, solve it directly. Combine Combine the solutions of the subproblems to obtain the solution to the original problem.
- 3. Advantages of Divideand Conquer Divide and conquer offers several benefits, making it a popular technique in algorithm design. 1 Efficiency It often leads to efficient algorithms, especially for problems that can be broken down into independent subproblems. 2 Parallelism Divide and conquer algorithms are well-suited for parallel processing, as subproblems can be solved concurrently. 3 Simplicity The recursive nature of divide and conquer can make algorithms easier to understand and implement.
- 4. Disadvantages of Divideand Conquer While highly effective, divide and conquer has certain drawbacks that need to be considered. Overhead The overhead of dividing and combining solutions can sometimes outweigh the benefits, especially for small problems. Memory Usage Recursive algorithms can use significant memory, as they store the state of each subproblem.
- 5. Applications of Divide andConquer Divide and conquer finds extensive use in various areas of computer science, showcasing its versatility. Sorting Algorithms Merge Sort, Quick Sort Searching Algorithms Binary Search Matrix Multiplication Strassen's Algorithm Closest Pair Problem Divide and Conquer Algorithm
- 6. Divide and Conquer Algorithms Severalwell-known algorithms are based on the divide and conquer principle, demonstrating its effectiveness in solving a wide range of problems. Merge Sort A sorting algorithm that divides the input list into two halves, recursively sorts each half, and then merges the sorted halves. Quick Sort Another efficient sorting algorithm that partitions the input list around a pivot element, recursively sorts the partitions, and then combines the sorted partitions. Binary Search A search algorithm that repeatedly divides the search space in half, effectively finding the desired element in a sorted list.
- 7. Implementing Divide and Conquer Theimplementation of divide and conquer algorithms typically involves recursion, allowing for a concise and elegant representation of the solution. Recursive Functions Recursive functions play a crucial role in implementing divide and conquer algorithms, breaking down the problem into smaller subproblems. Base Cases Base cases are essential for preventing infinite recursion, ensuring that the algorithm terminates correctly. Combine Solutions After recursively solving subproblems, the solutions are combined to obtain the final solution.
- 8. Conclusion and Key Takeaways Divideand conquer is a powerful and versatile problem- solving technique with broad applications in computer science. By recursively breaking down problems into smaller subproblems, divide and conquer often leads to efficient and elegant algorithms.