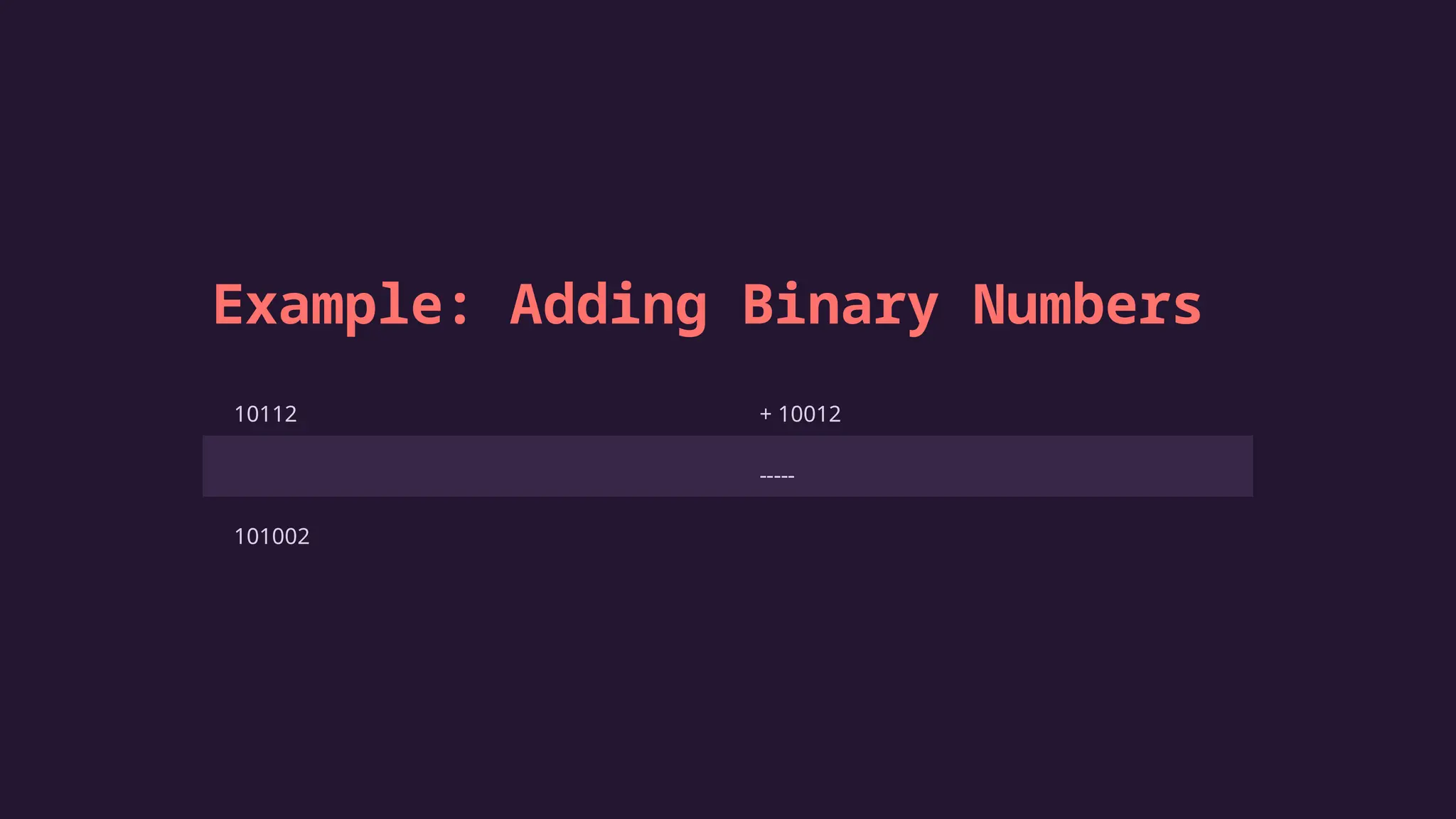
The document explains binary arithmetic, a mathematical system using only 0 and 1, which is essential for modern computing. It covers fundamental concepts including place values, binary operations (addition, subtraction, multiplication, and division), and practical applications such as digital computers and data storage. Understanding binary arithmetic is crucial for anyone interested in computing technology.

1. GARDENIA PUBLIC SCHOOL
Summer holiday project
Binary Arithmetic Operations
Class:7th
Su
Subject : Computer
Subject:Computer

2. Introduction to
Binary
Arithmetic
Binary arithmetic is a system of mathematics that uses only two
digits: 0 and 1. This system is fundamental to modern computing, as
computers use binary to represent and process information.

3. Understanding Binary Numbers
1 Place Values
Each position in a binary number
represents a power of two, starting from
the rightmost digit as 20, then 21, 22,
and so on.
2 Base-2 System
Binary numbers use base-2, meaning
each digit can be either 0 or 1, unlike
decimal numbers which use base-10 (0-
9).
3 Conversion to Decimal
To convert a binary number to decimal,
multiply each digit by its corresponding
power of two and add the results.
4 Example
The binary number 10112 is equivalent
to 1*23 + 0*22 + 1*21 + 1*20 = 8 + 0 + 2
+ 1 = 1110 in decimal.

4. Basic Binary Operations:
Addition, Subtraction
Binary Addition
Similar to decimal addition, carry-overs occur
when the sum of two digits exceeds 1. The
carry-over is added to the next digit.
1. 0 + 0 = 0
2. 0 + 1 = 1
3. 1 + 0 = 1
4. 1 + 1 = 0 (carry-over 1)
Binary Subtraction
Borrowing is necessary when subtracting a
larger digit from a smaller digit. The
borrowing is done from the next digit, making
it a 0 and adding 2 to the current digit.
1. 0 - 0 = 0
2. 1 - 0 = 1
3. 1 - 1 = 0
4. 0 - 1 = 1 (borrow 1)

5. Example: Adding Binary Numbers
10112 + 10012
-----
101002

6. Example: Subtracting Binary Numbers
11012 - 10102
-----
00112

7. Binary Multiplication and Division
Multiplication
Similar to decimal multiplication, binary
multiplication involves multiplying each digit
of the multiplicand by the multiplier and then
adding the partial products.
1. 0 * 0 = 0
2. 0 * 1 = 0
3. 1 * 0 = 0
4. 1 * 1 = 1
Division
Binary division works by repeatedly
subtracting the divisor from the dividend until
the remainder is less than the divisor.

8. Applications of Binary Arithmetic
Digital
Computers
Computers rely on
binary arithmetic
to perform
calculations, store
data, and execute
programs.
Digital
Logic
Circuits
Binary logic gates,
such as AND, OR,
and NOT, are built
using binary
arithmetic to
process signals.
Data
Transmission
Binary codes are
used in
communication
networks to
transmit digital
information,
ensuring accuracy
and efficiency.
Data Storage
Binary codes are
used in hard
drives, flash drives,
and other storage
devices to
represent data in a
format that can be
easily accessed by
computers.

9. Conclusion
Binary arithmetic is a foundational concept in computer science, providing the basis for how
computers process and understand information. Its simplicity and efficiency make it essential for
the operation of modern technology. The understanding of binary arithmetic is crucial for anyone
seeking to delve deeper into the world of computing.