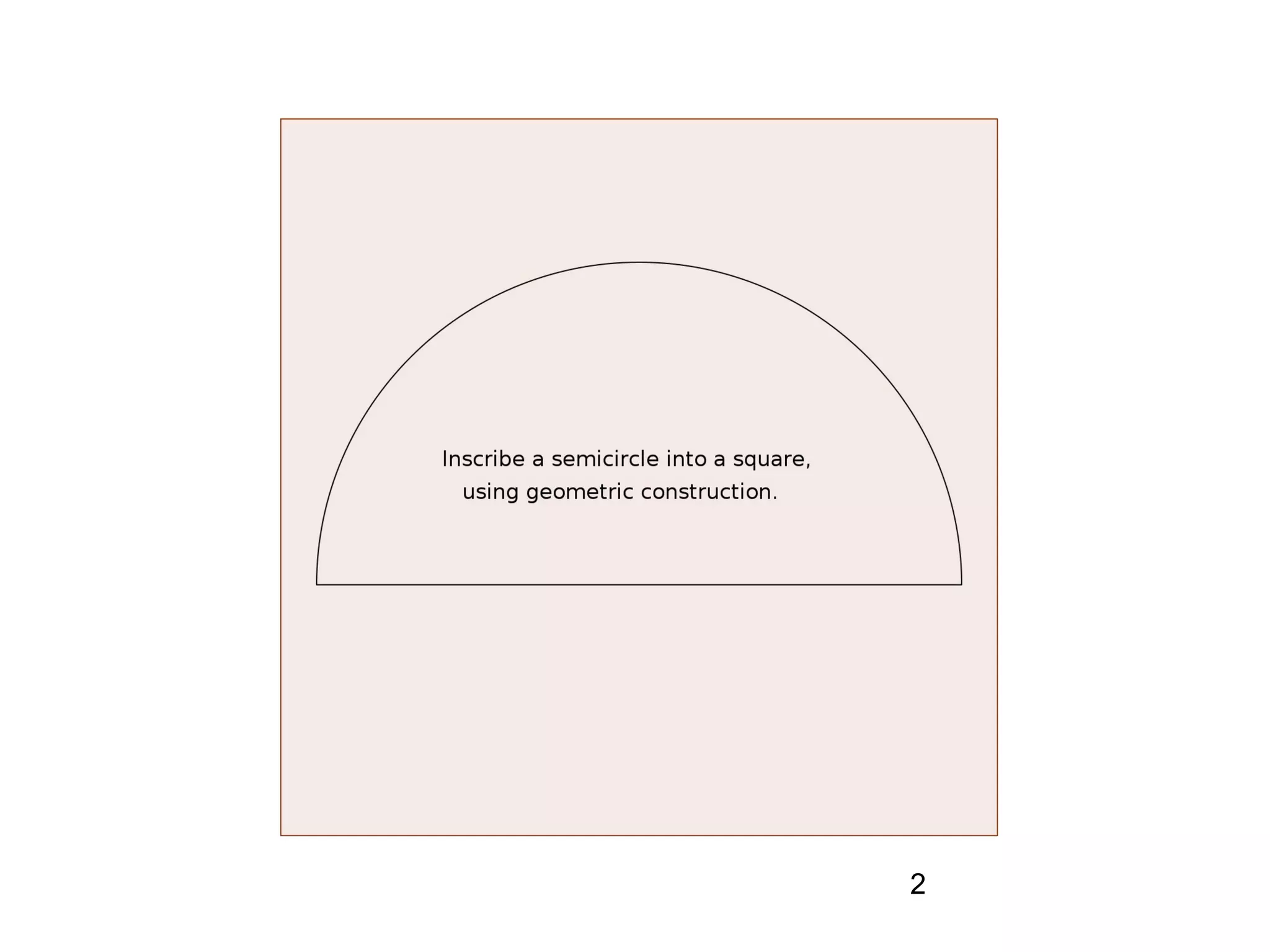
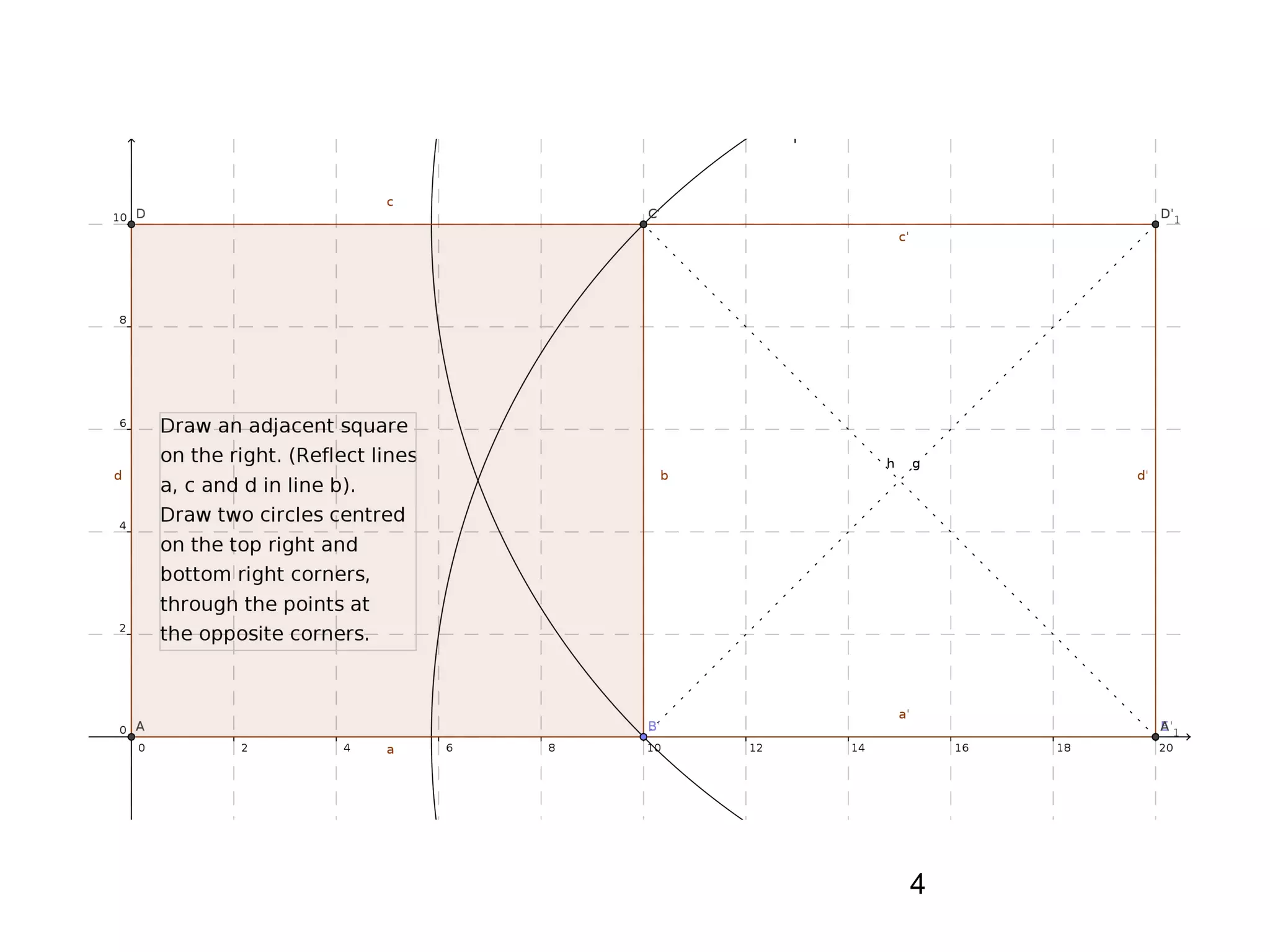
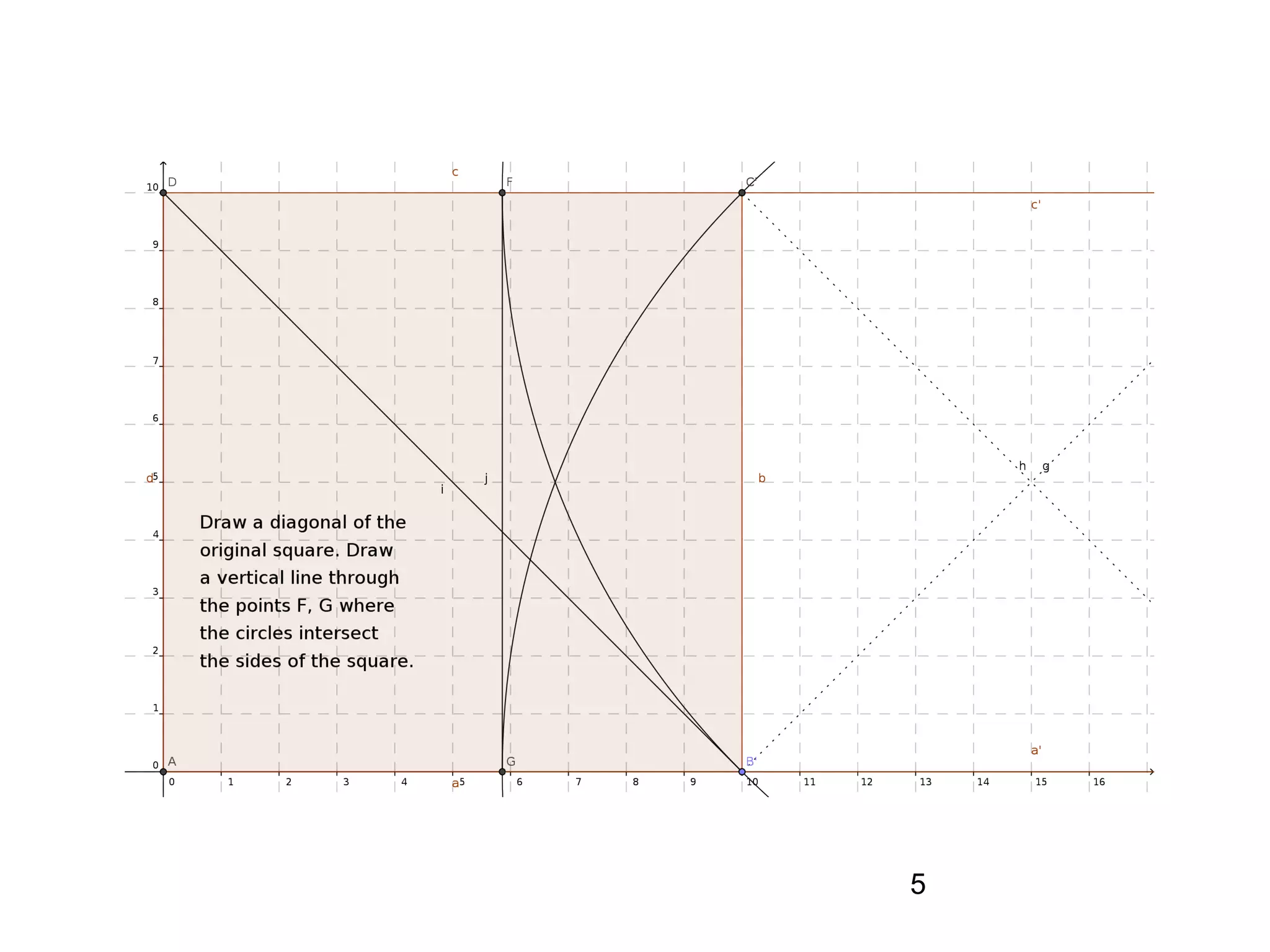
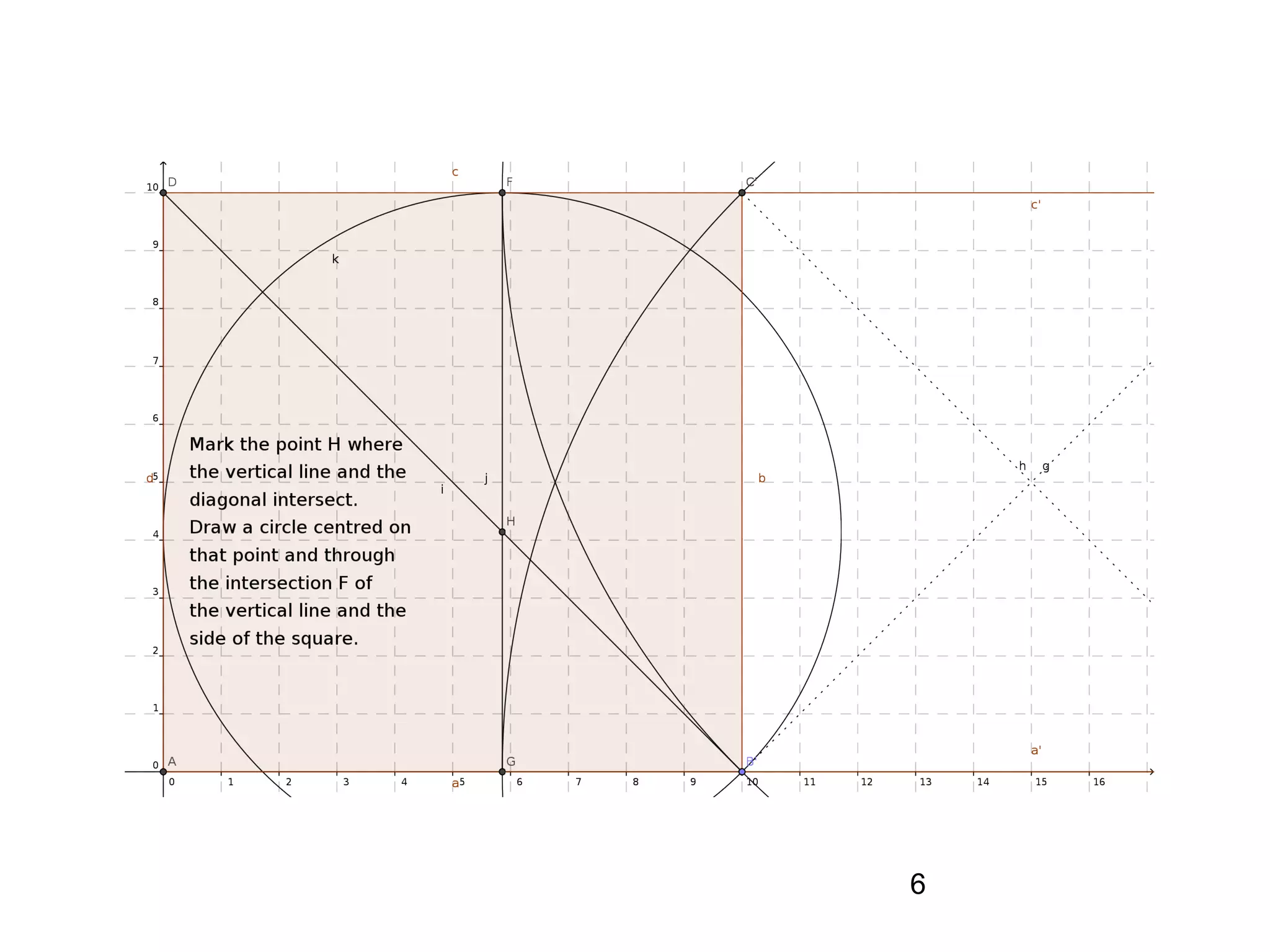
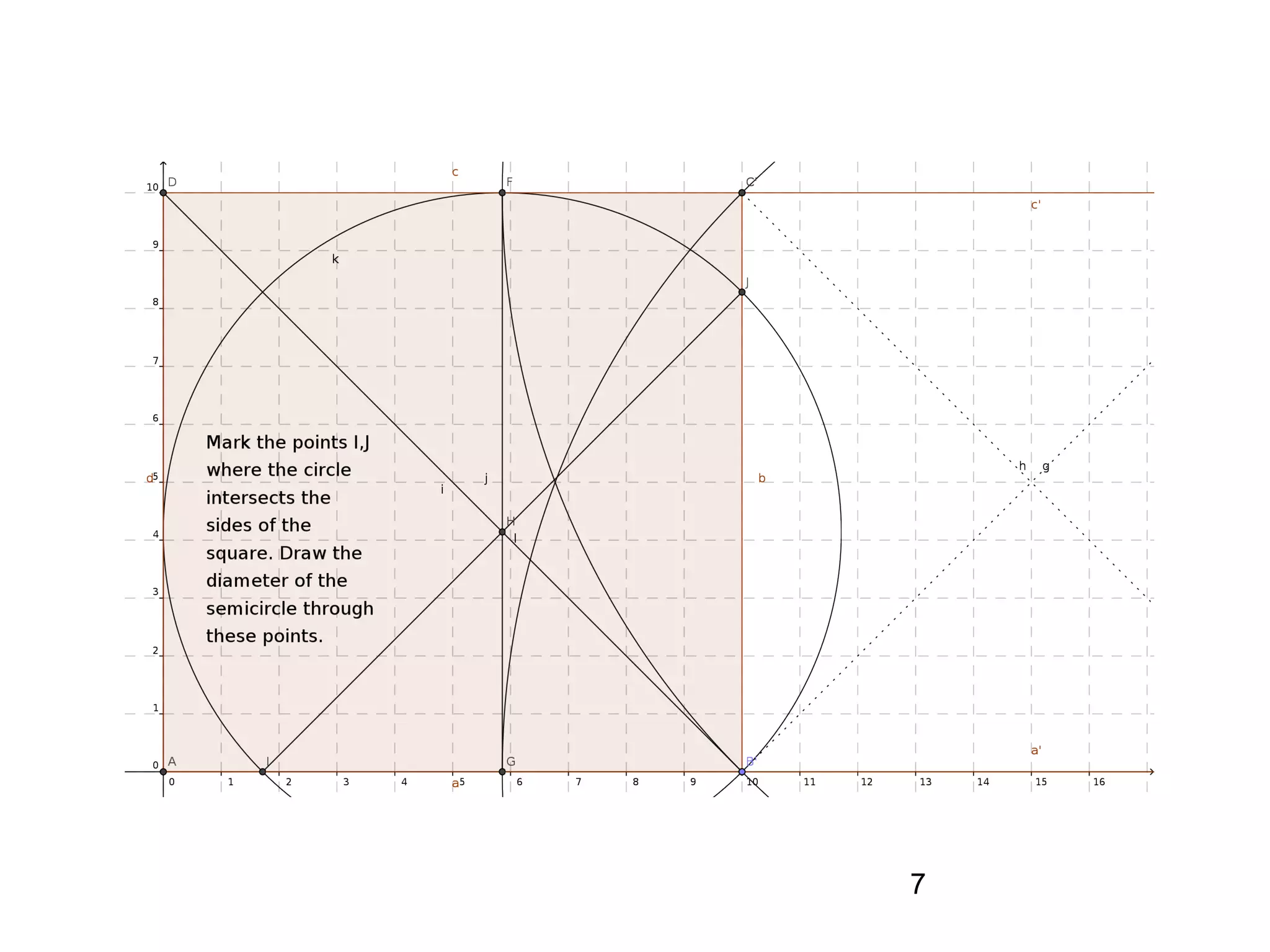
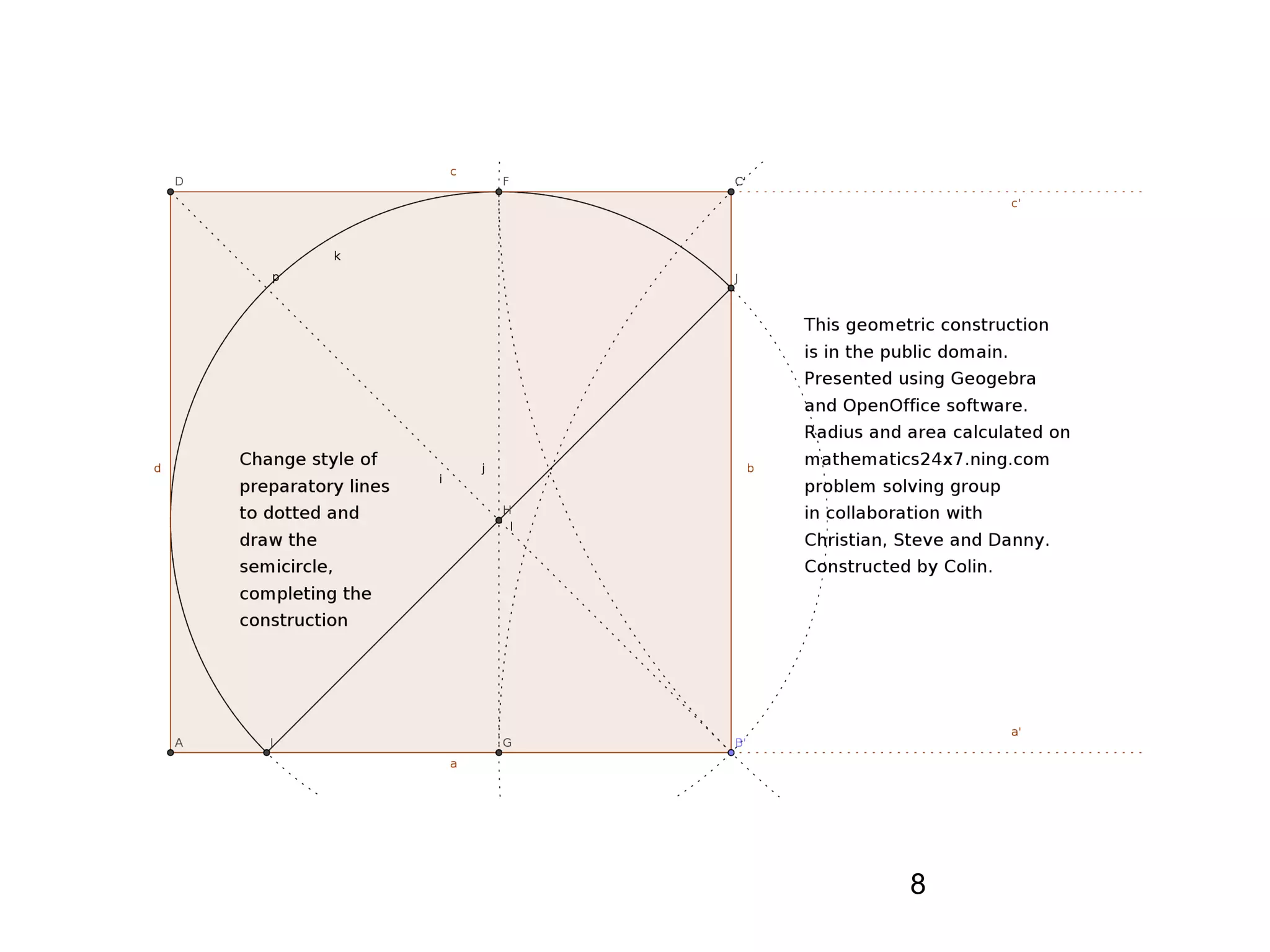
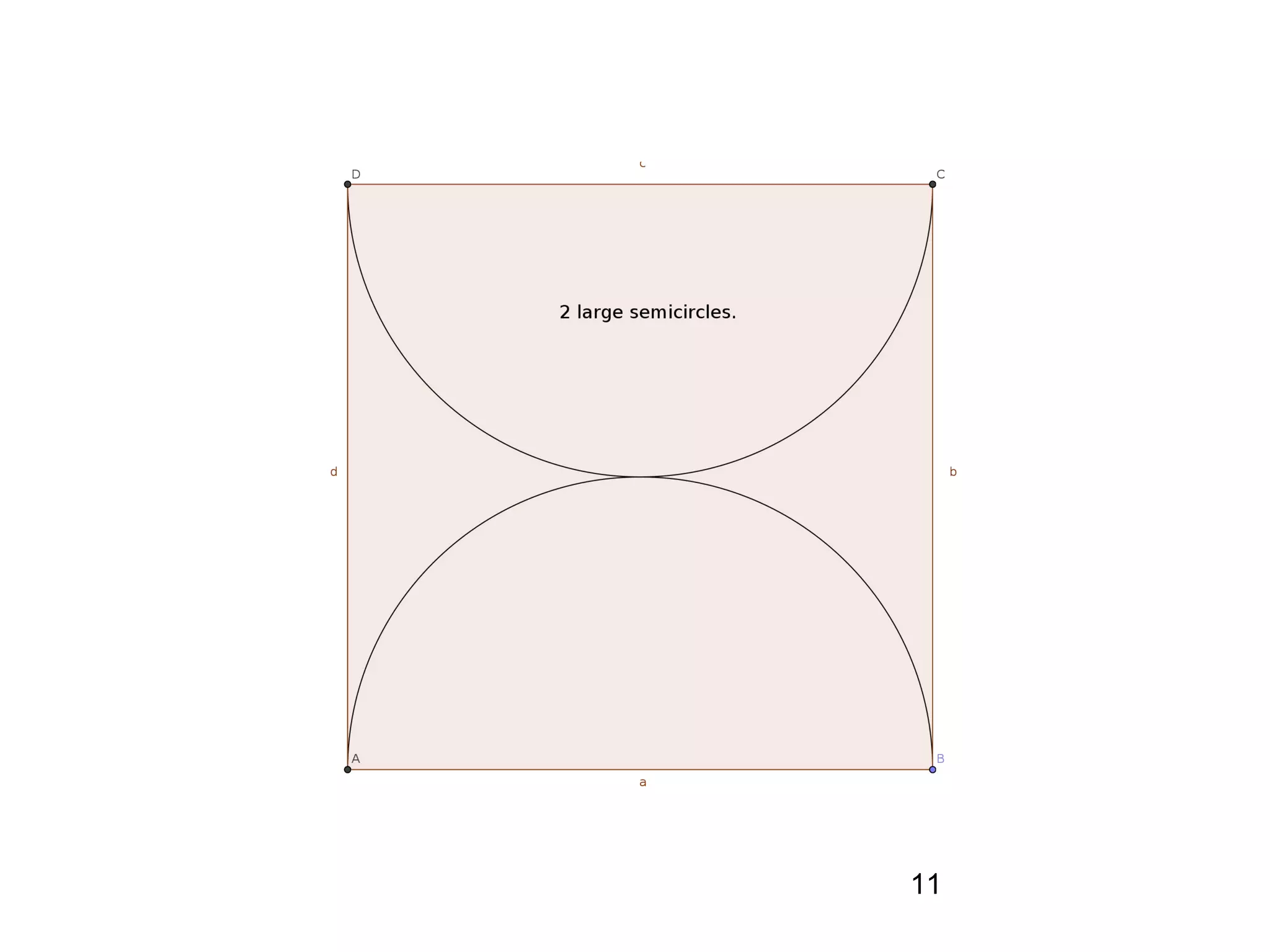
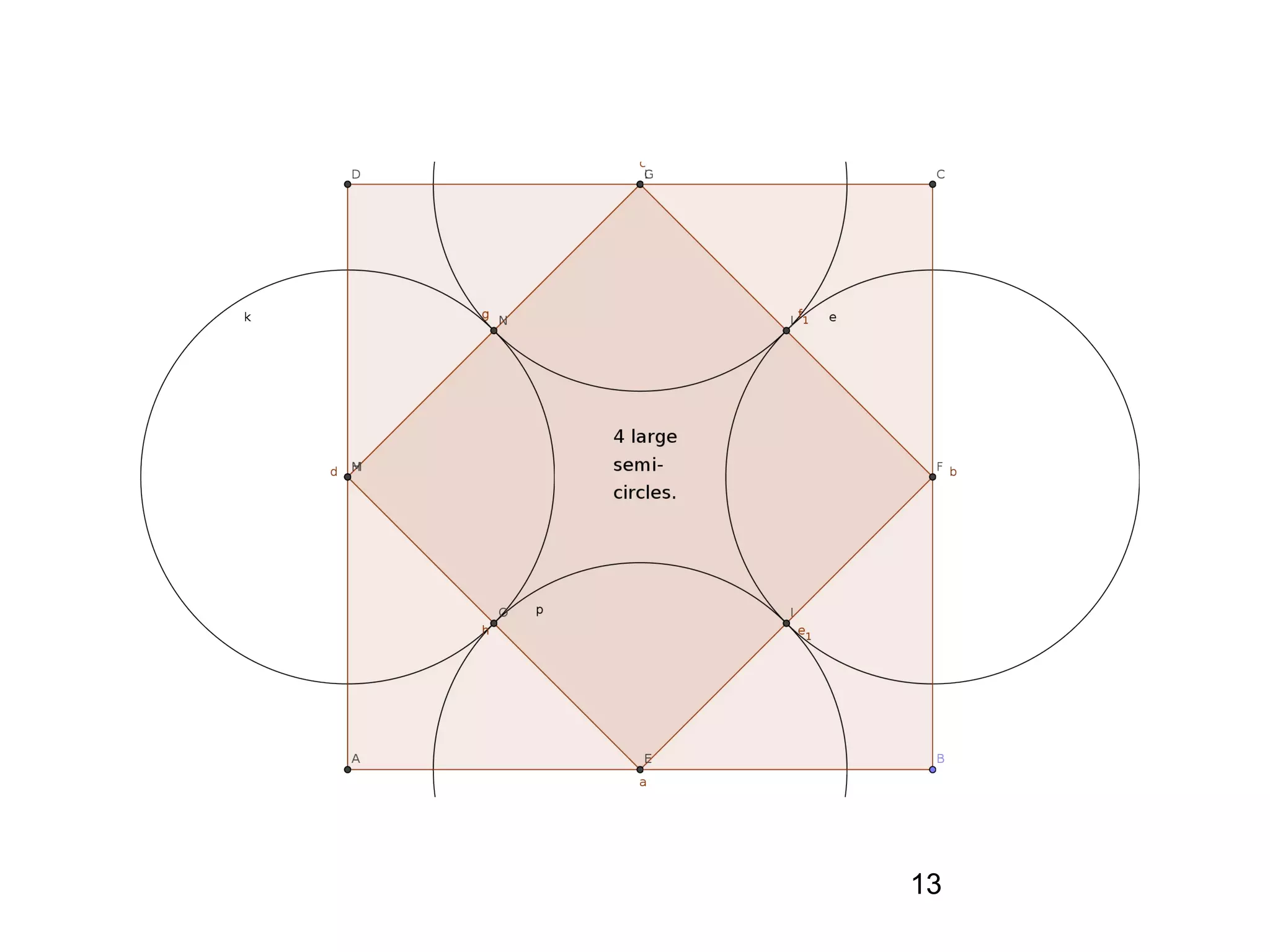
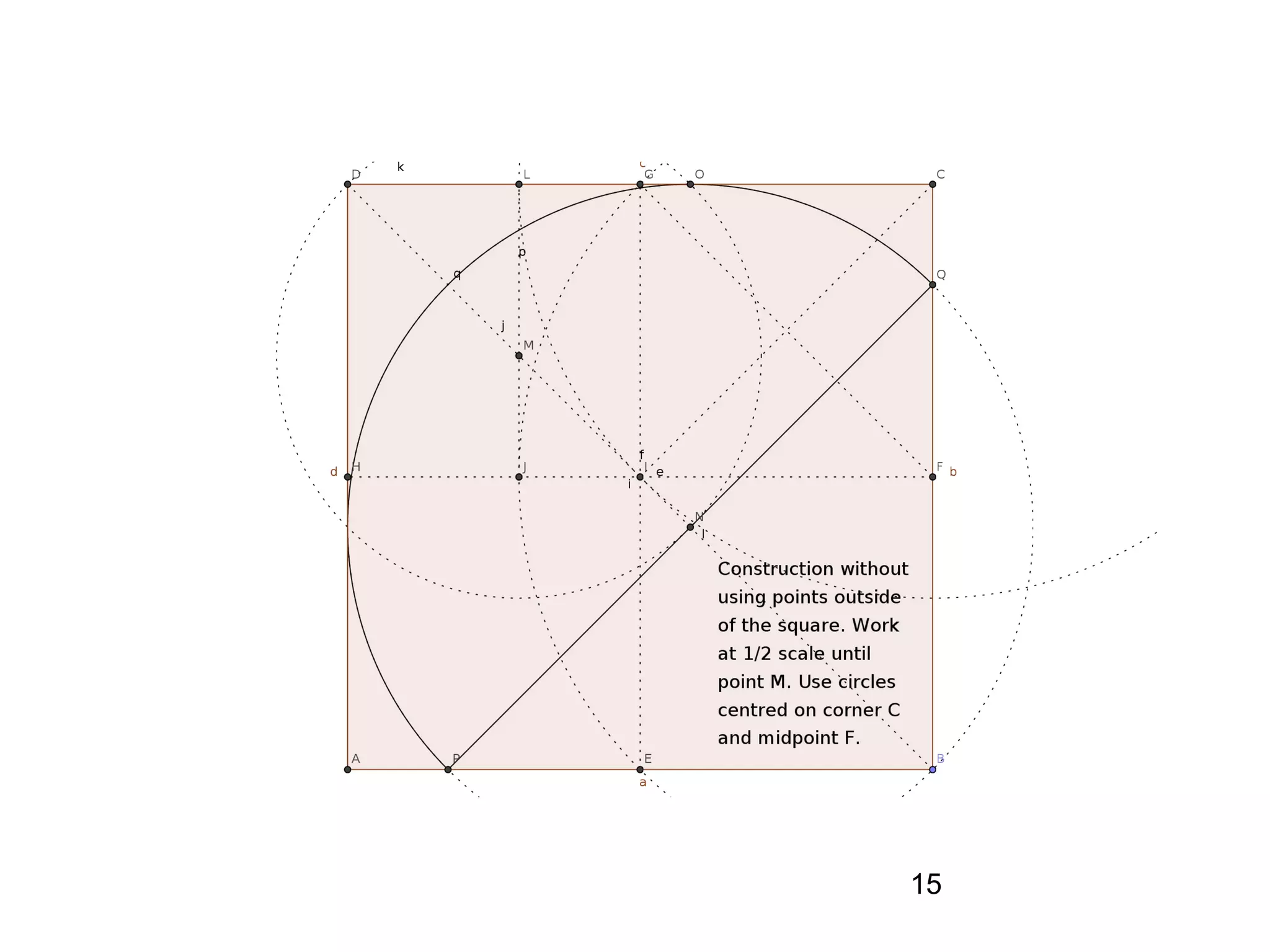
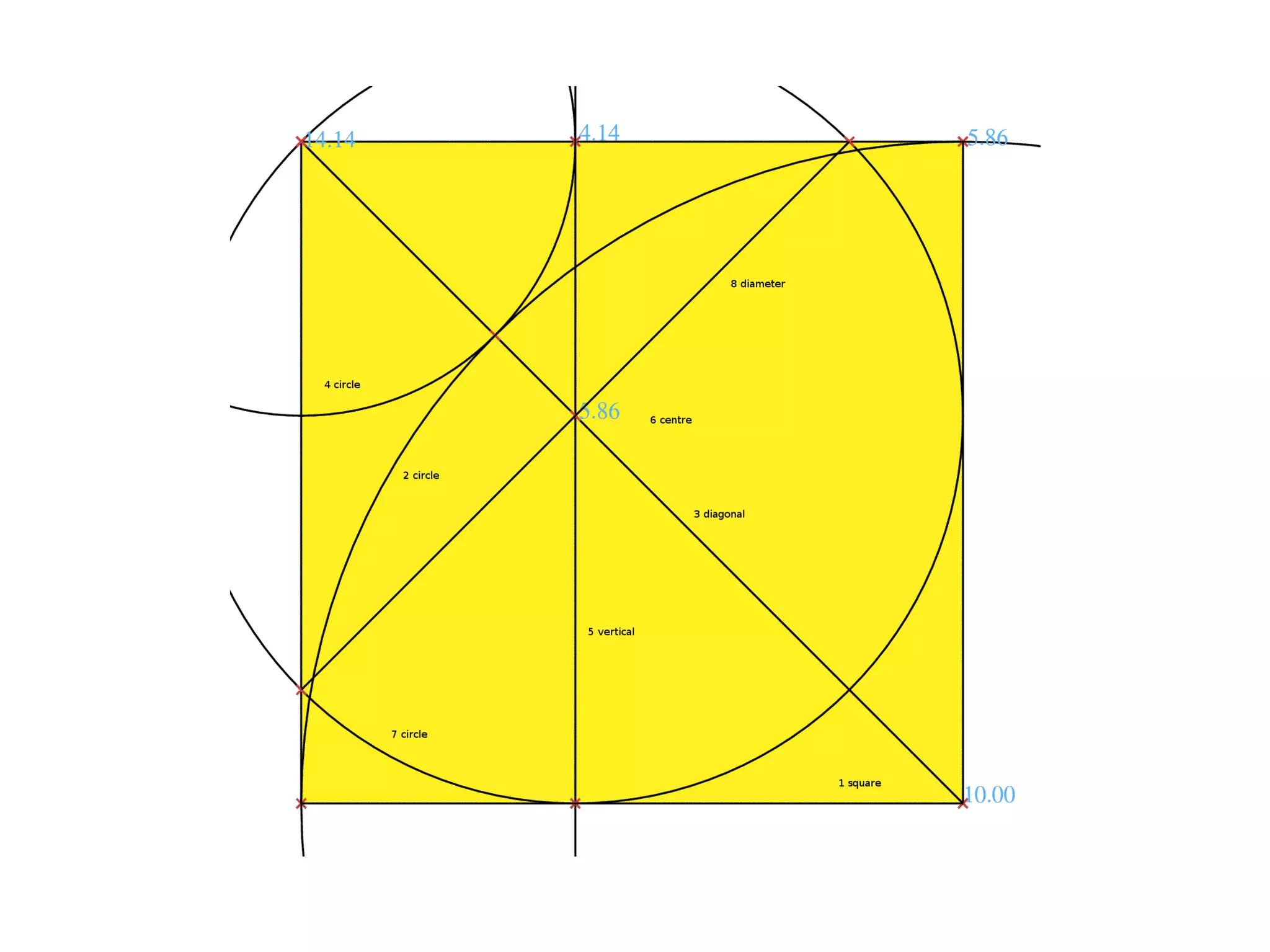
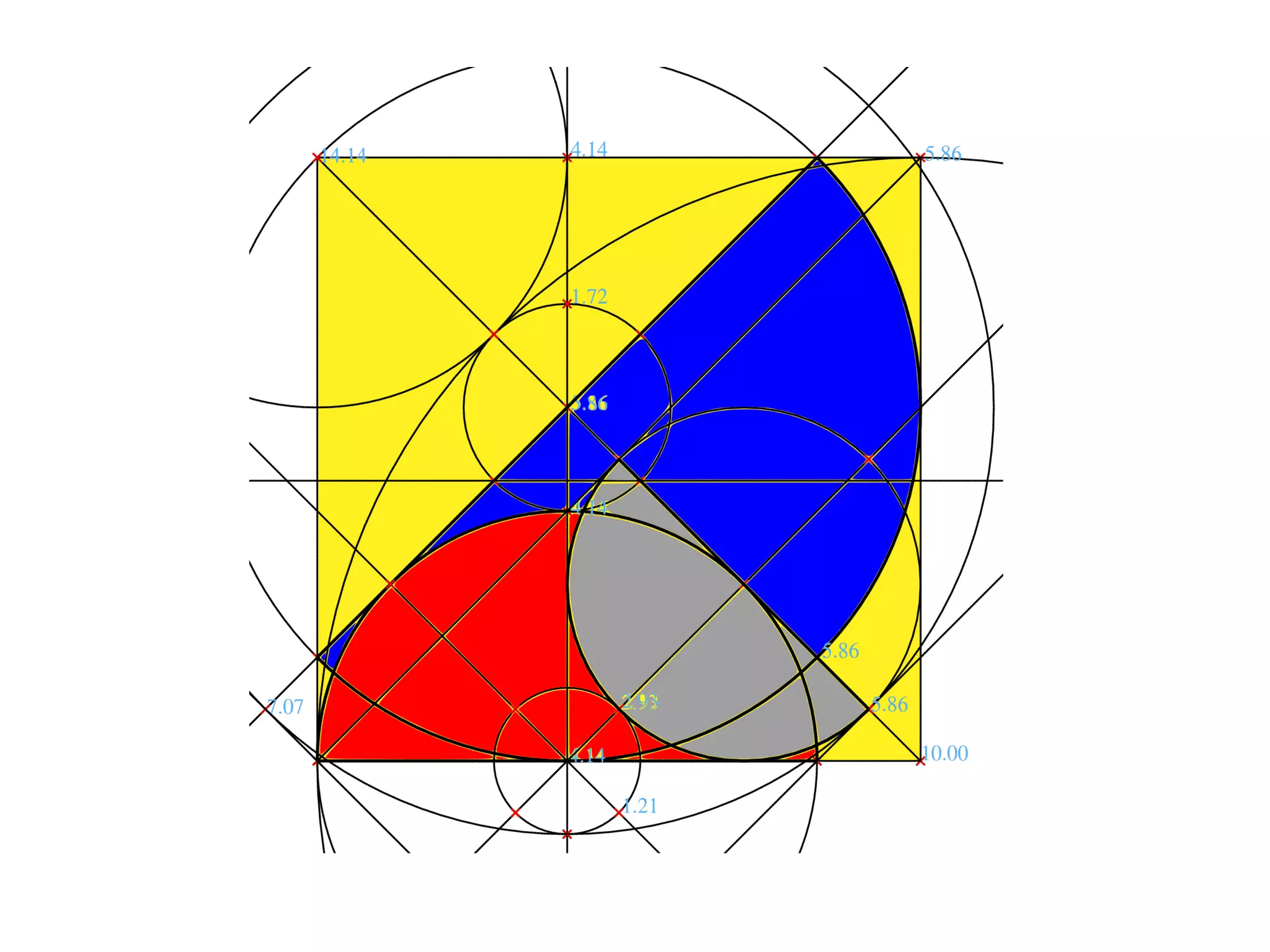
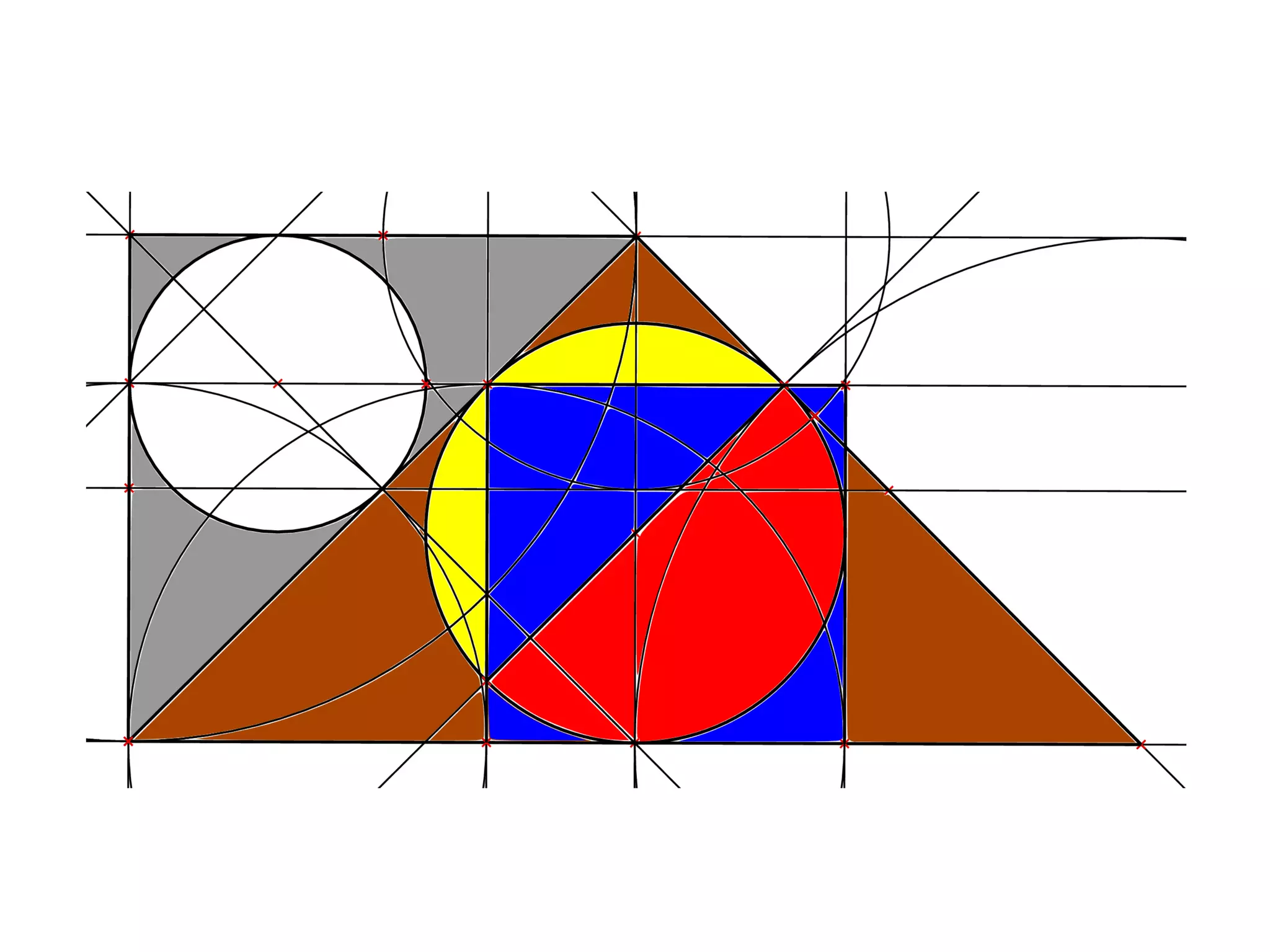
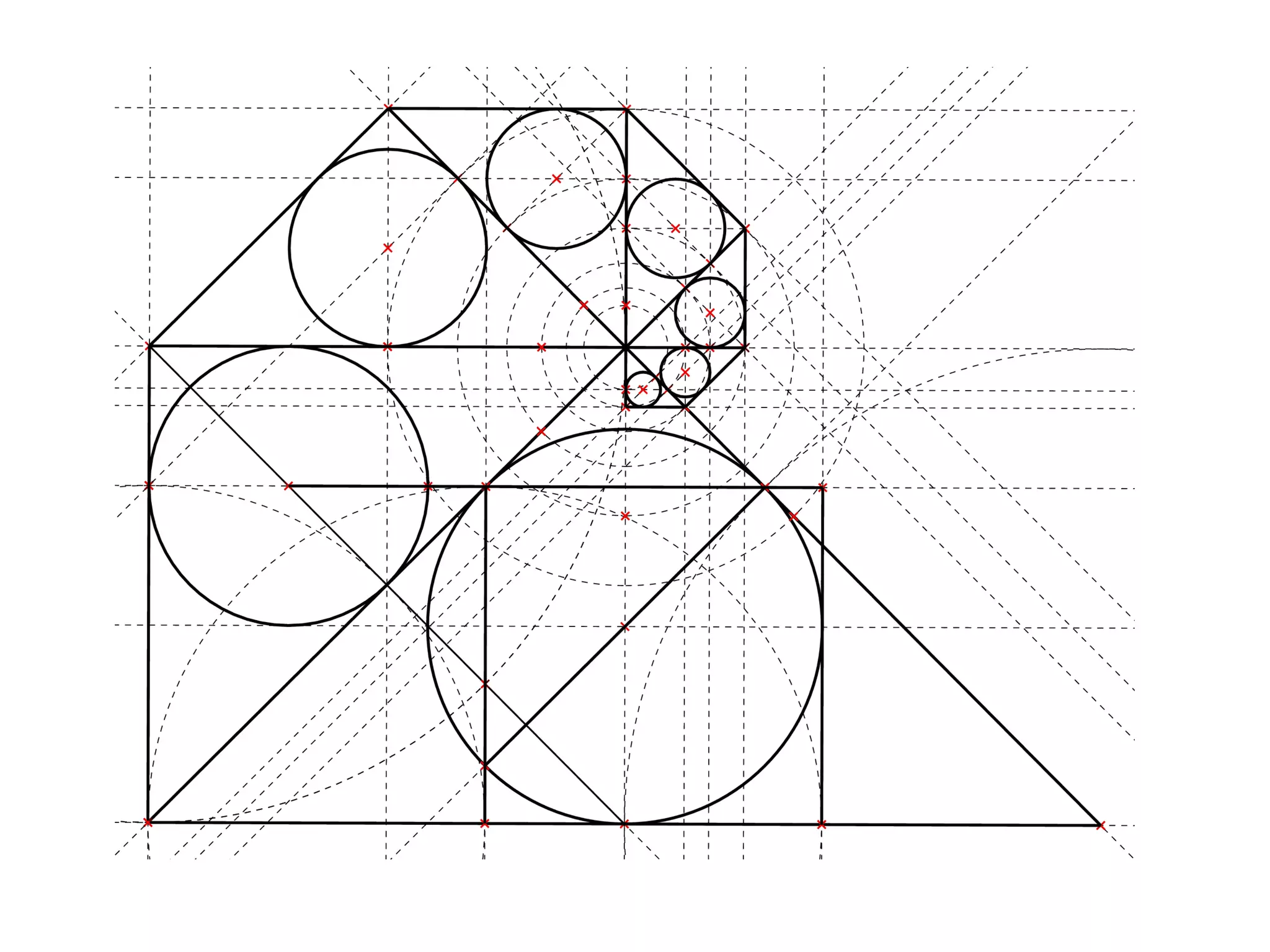
The document provides a geometric construction for inscribing a semicircle within a square and includes definitions, exercises, and alternative methods for achieving the construction. It highlights the relationship between inscribed figures and presents recursive techniques for creating smaller semicircles, as well as explaining connections with isosceles right triangles. Various geometric designs and software tools are mentioned to enhance understanding and application of the concepts presented.

1. Inscribe a Semicircle in a Square
Using Geometric Construction
A slideshow showing the
steps of construction

2. 2

3. Definition of Inscribed Figure
In geometry, an inscribed planar shape or solid
is one that is enclosed by and "fits snugly"
inside another geometric shape or solid.
Specifically, at all points where figures meet,
their edges must lie tangent. There must be
no object similar to the inscribed object but
larger and also enclosed by the outer figure.
From Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Inscribed_figure
3

4. 4

5. 5

6. 6

7. 7

8. 8

9. Exercise 1: Identify other large
semicircles that fit in a square or a
rectangle.
Exercise 2: Draw circles and regular
polygons on paper using a pair of
compasses and a ruler.
Exercise 3: Find an alternative
procedure for inscribing a semicircle
in a square.
Exercise 4: Draw large geometric
shapes on a playground using chalk,
string and straight lengths of wood.
Exercise 5: Learn to use geometry
software on a personal computer.
9

10. Exercise 1.
Identify other large semicircles that
fit in a square.
Some solutions follow:
10

11. 11

12. 12

13. 13

14. Exercise 3.
Find an alternative procedure for
inscribing a semicircle in a square.
Hint: One method is to use the
previous solution at half scale.
14

15. 15

16. Exercise 3.
Alternative procedure for geometric
construction of the inscribed semicircle.
This solution was found by Linda
Fahlberg-Stojanovska, as described in
her geometry paper at:
http://geogebrawiki.pbworks.com/ciit10
The sequence of steps is numbered.

18. Calculation of Area of
Semicircle
Inscribed in Unit Square
The unit square has a width
of 1. Divide this into two parts
at the centre of the semicircle.
Left of the origin, in the 9 o'clock
or negative-x direction,
the distance to the side of the
square is r, the radius.
Right of the origin in the
3 o'clock or x direction
the distance is r/sqrt(2), by
pythagoras's theorem on
the 45 degree triangle.
This expression can be
factorised as follows to
calculate the radius r :
18

19. Recursively Inscribed Semicircles
Use compass and straightedge construction to
generate recursively smaller inscribed semicircles,
each half the area of the previous semicircle. The
blue and red shapes are related by translation,
rotation and scale. The construction is self similar,
i.e. reproducible at any magnification or reduction
that is a multiple of the square root of two. Notice
some coincidences: The diameter of the second
semicircle lies on the side of the first square, and the
corner of the third semicircle is the centre of the
square. The figure also contains a circle inscribed in
an isosceles right triangle.

21. Circles Inscribed in Isosceles Right Triangles
There is a relationship between a circle
inscribed in an isosceles right triangle, and a
semicircle inscribed in a square. Beginning
with the brown triangle, we add a reduced
grey triangle. Notice that the centre of the
circle in the small triangle lies on the line that
defines the blue square circumscribing the
red semicircle in the large triangle.

23. Scorpion
This “Scorpion” is an extension of the
previous construction, by recursively
adding isosceles right triangle,
hypotenuse against short side. The
inscribed circles form a decreasing
spiral, each one half the area of the
previous one. The construction would
be self similar, but for the largest
triangle, which is oriented 90 degrees
off of its proper position in the spiral.

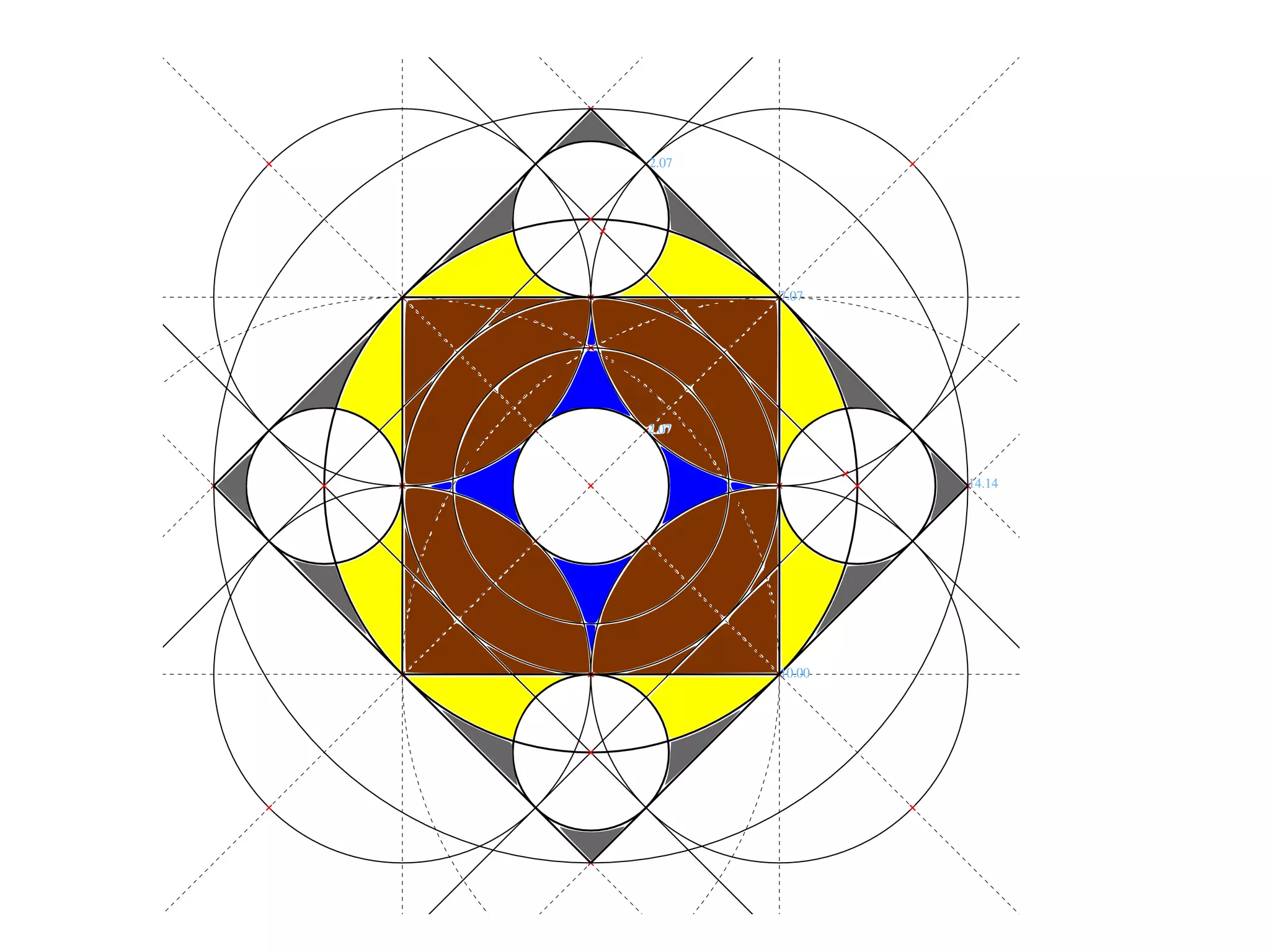
25. Circles on Circles
A [brown] square is inscribed diagonally in a [grey]
square, four [grey and yellow] isosceles right triangles
remain. When [white] circles are inscribed in those
triangles, their centres lie on the circumference of the
[yellow] circle that inscribes the outer square. When
four [brown] quarter circles are inscribed in the inner
square, corner on corner, a centred [white] circle,
inscribed in the [blue] gap between them, is of the
same size as those inscribing the isosceles right
triangles. These coincidences arise from the ratio of
length of the diagonal to the side of a square, which is
the square root of two.

27. Circles on Circles Extended
The construction can be extended by
circumscribing another circle and square
around the outer diagonal square.
This series of constructions began by
studying a semicircle inscribed in a square. If
you look carefully, you can see semicircles
inscribed in squares, and circles inscribed in
quarter circles.
A suggested exercise is to inscribe four
circles in a circle, using compass and
straightedge, or equivalent PC software.

30. This slide show and included geometric
Constructions are in the public domain.
Drawn using Geogebra and Dr. Geo
Open source geometry software.
Radius and area of inscribed semicircle
calculated on the mathematics24x7.ning.com
problem solving group in collaboration with
Christian, Steve and Danny. Alternative
method of inscription discovered by Linda.
Slideshow and constructions by Colin.
30