This research proposal aims to develop an improved method for identifying the most influential nodes in complex networks by decomposing graphs into subgraphs and utilizing various measures to rank node power. It incorporates entropy theory and examines relationships between nodes, specifically focusing on triangles formed in the network to establish influence and control. The findings suggest that a comprehensive approach combining multiple measures is more effective for understanding node importance and influence propagation.

1. Identifying Most Powerful Node In Complex Networks:
A Triangle Graph Decomposition Approach
Research Proposal for Master Degree
Student ID：
Name： Auwal Tijjani Amshi
1
School of Software

2. Content
1. Introduction & Objective
2. Background
3. Method Description
4. Summary
2
6/13/2024
School of Software

3. Introduction
This research is aimed to introduce an improve method of identifying most powerful
node using by decomposing graph into subgraphs (trust cycle) and using three
different measures result to rank the most powerful node.
By adopting entropy theory and measuring the constraint in the network, the proposed
method can be well qualified to optimize social influence; and also can be useful for
detecting powerful nodes.
By quantifying the power influence of a node on its neighbors and the control influence
on the network, the proposed methods characterize associations among node pairs
in form of triangle connection/relationship and capture the process of influence
propagation.
3
6/13/2024
School of Software

4. Introduction
The objective of this research is to combine node power and control, so as to fine
the total influence of a given set of nodes, by measure of the structural
information content of a graph and explored its mathematical properties.
4
6/13/2024
School of Software

5. Background
5
6/13/2024
School of Software

6. Background
Neighborhood-based methods
Therefore, many researchers used the approach of counting directly the number of
node immediate neighbors, which give degree centrality [2, 3].
***
Some researchers like [4] Consider community overlapping and network structure
toward identifying influential node in a network.
***
Burt el al. [5] used network constrain coefficient to measure the constraint imposed by
forming a structure hole.
6
6/13/2024
School of Software

7. Background
Path-based methods
The node that can spread information faster is more important, which can be identified
by the path of propagation [6] such as betweenness centrality and Closeness
centrality.
***
Generally speaking node with largest Closeness centrality: has the strongest control
over the information flow. Meanwhile node with smallest closeness centrality is the
best for information flow.
***
In [7] Katz introduced a measure of centrality known as Katz centrality which
computed influence by taking into consideration the number of walks between a
pair of nodes.
7
6/13/2024
School of Software

8. Background
Entropy-based methods
Information theory deals with the quantification of information and has been
successfully applied in a wide range of fields. [9]
Motivated by the original work owing to Shannon [9, 10], first studied the relations
between the topological properties of graphs and their information content and
introduced the concept of graph entropy.
8
6/13/2024
School of Software

9. Method Description
9
6/13/2024
School of Software

10. Method
10
6/13/2024
School of Software

11. Subgraph G’ Construction And Sampling
Given a simple graph G (V, E) as an experimental graph, with V set of edges and E set of
edges.
11
6/13/2024
School of Software

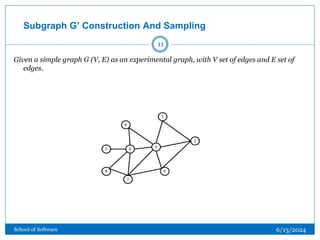
12. Subgraph G’ Construction And Sampling
Let take node 1 and node 9 as example.
[a] [b]
Figure [a] represent the sub-graph constructed by node 1 and [b] represent sub-graph
constructed by node 9.
12
6/13/2024
School of Software

13. Reduction of Data
Given set of subgraph G’ G with N number of node and TRi G as number of triangles form
by node i and by definition TRi 0 which can be express by:
Where N is the total number of node in the sub-graph, sdegj is the degree of node j. If the
condition is false then sub-graph will be consider as not relevant to this research.
(3)
13
6/13/2024
School of Software

14. Alg0rithm 1: Fl0wchart
Sampling of Sub graphs
S = {set of subgraph G’i}
TR = selection constrain
Sv = {set of valid sample}
14
6/13/2024
School of Software

15. Preliminaries
15
6/13/2024
School of Software

16. Definition 2: Tr-Centrality (TC)
The tr-centrality of node i on its one-hop neighbors, denoted as which can be represent
with a constrain:
CTC=
Where
nv is the total number of nodes in sub-graph G’,
ntr is the number of triangle in graph G’,
M= {1, 2… m} and
Then we added to the equation which is called the distinguishing coefficient to insure
.
(8)
(9)
16
6/13/2024
School of Software

17. Definition 1 : Node Entropy(PI)
[19] defined an information functional based on degree powers of graphs. In this
research, an approach is adopted [6] to get the tuple by using degree centrality. The
adopted equation below is an information functional based which reflect the degree
power of graph gives:
(6)
(7)
17
6/13/2024
School of Software

18. Definition 3: Node Constraint(CC)
Assume that network subgraph of graph G is an undirected network with nodes and edges.
The edge between node vi and vj is eij. And it importance is defining [20] as:
Where
U- reflect the connection ability of edge eij. ki and kj are the degree of node vi and vj.
P- represents the number of triangle where edge eij is part of
The alternative index of edge eij is define as:
(10)
(11)
18
6/13/2024
School of Software

19. Definition 3: Node Constraint(CC)
To calculate the constraint coefficient with respect to each relationship in the network graph. By
adopting Burt el al [4, 5] measure of structural holes. We can sum of each connection's constraints
Cij which is define as:
Pij is the proportion of edge weights from i to j which define as:
 Where EIij measure the edge between i and j.
 Assume there exists an indirect path , then the product of proportion of edge weights between i to q,
and q to j will be the total amount of indirect influence from i to j.
(12)
(13)
19
6/13/2024
School of Software

20. Definition 4: Total Power of Node(TPN)
To perform the comprehensive evaluation of node influences, it is necessary to construct a
model by combining three measures together. Here, we define this model as a Total
power of node, TPN.
where:
PI- compute the node local entropy.
TC- compute the node local trust.
CC- compute the node constrain coefficient.
(14)
(15)
20
6/13/2024
School of Software

21. Model Flowchart
G’i subgraph of i
Sv = {set of valid samples}
CTC= tr-centrality constrain
TC=tr-centrality
PI=graph entropy
CC= Node constrain.
TPN= total power of node.
21
6/13/2024
School of Software

22. Summary
 Each measure has its own sense to judge the node’s importance for information
spreading and also ignores some aspects of influence measurement. For this reason,
comprehensively considering the discussed three measures seems to be more rational
than the separate application.
 In this research the measure of power of node is in terms of trust in the node network.
The more triangle form by a given node the more we assumed the more powerful the
node is.
 In addition those who have more triangles, the nodes who serve as structure hole are
powerful because information can easily pass-through those nodes which implies there
exist a strong trust within their local network.
22
6/13/2024
School of Software

23. Thank You
23
6/13/2024
School of Software