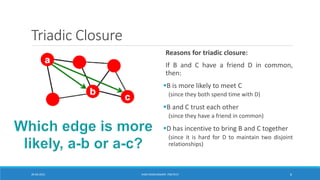
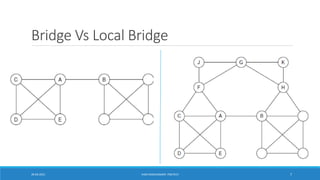
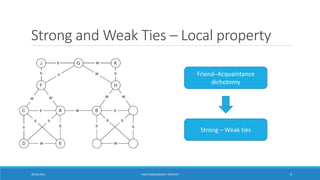
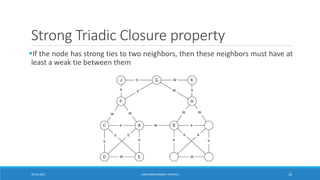
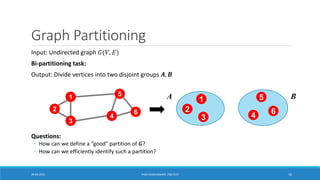
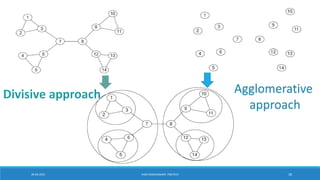
This document discusses methods for social network analysis, including community detection algorithms. It explains that community detection aims to partition a network into densely connected groups of nodes with fewer connections between groups. The document describes divisive and agglomerative approaches, including the Girvan-Newman algorithm and modularity optimization. It also discusses how to compute edge betweenness centrality and select the optimal number of communities using modularity.




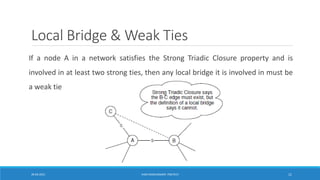
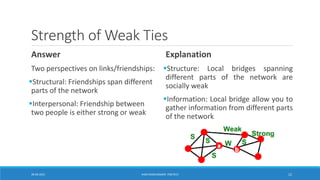
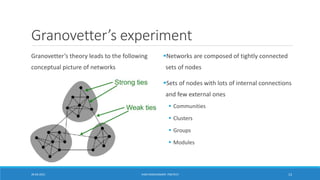
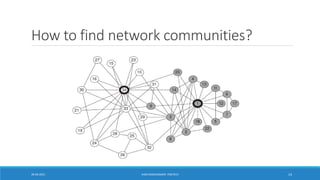



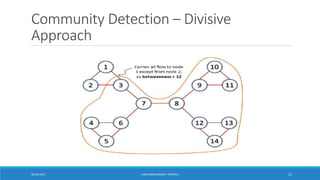
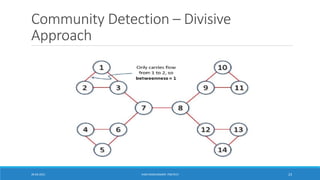
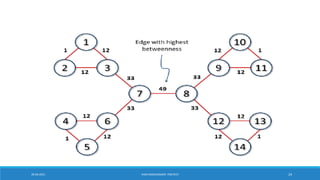
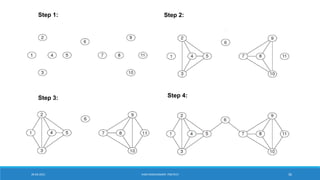
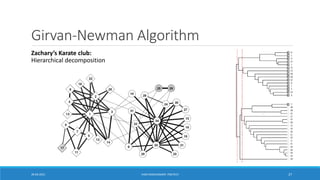
![Girvan-Newman Algorithm
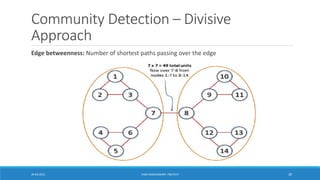
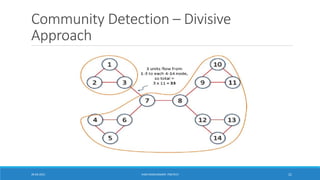
▪Divisive hierarchical clustering based on the notion of edge betweenness
▪Undirected unweighted networks
▪Algorithm:
• Repeat until no edges are left:
o Calculate betweenness of edges
o Remove edges with highest betweenness
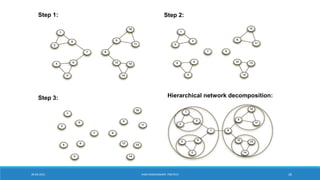
▪ Connected components are communities
▪ Gives a hierarchical decomposition of the network
[Girvan-Newman ‘02]
20-04-2021 VANI KANDHASAMY, PSGTECH 25](https://image.slidesharecdn.com/unit3a-210420092315/85/Community-detection-Part1-25-320.jpg)

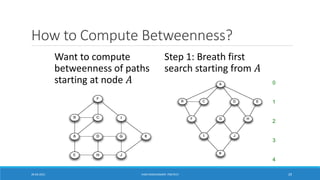
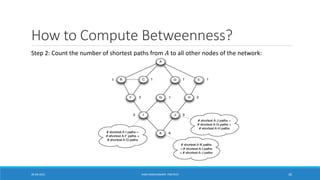
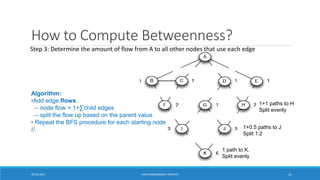
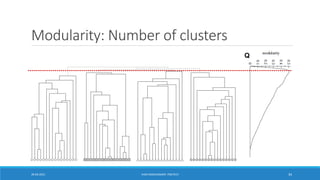
![How to select the number of clusters?
Define: Modularity 𝑸
A measure of how well a network is partitioned into communities
Given a partitioning of the network into groups 𝒔 𝑺:
Q ∑s S [ (# edges within group s) – (expected # edges within group s) ]
Null / Erdos-Renyi model
20-04-2021 VANI KANDHASAMY, PSGTECH 32](https://image.slidesharecdn.com/unit3a-210420092315/85/Community-detection-Part1-32-320.jpg)
![Modularity values take range [−1,1]
0.3-0.7<Q means significant community structure
20-04-2021 VANI KANDHASAMY, PSGTECH 33](https://image.slidesharecdn.com/unit3a-210420092315/85/Community-detection-Part1-33-320.jpg)