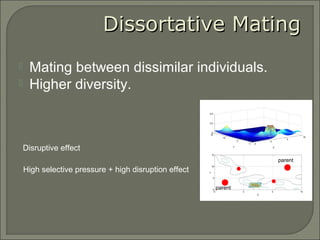
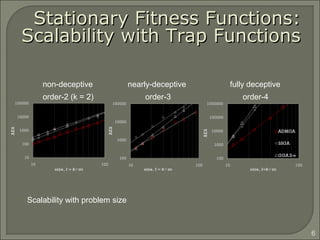
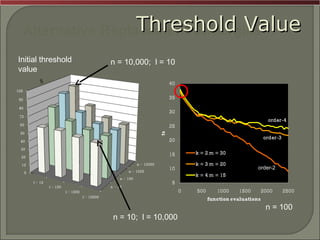
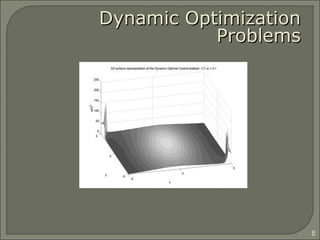
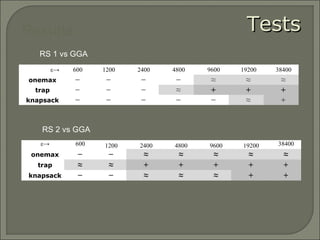
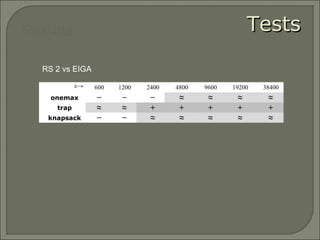
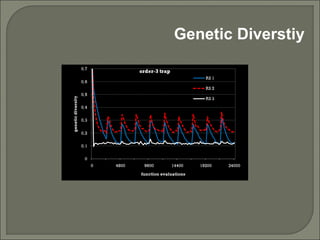
This document investigates replacement strategies for the Adaptive Dissortative Mating Genetic Algorithm (ADMGA) to improve its performance on dynamic optimization problems where the optimal solution changes over time. It compares the original ADMGA replacement strategy of selecting offspring and best parents to strategies that incorporate mutated copies of old solutions or the best solution. Testing on benchmark problems with different rates of change shows strategies using mutated old solutions outperform the standard genetic algorithm and are competitive with the estimation of distribution algorithm on faster changing problems.

1. INVESTIGATING REPLACEMENT STRATEGIES
FOR THE
ADAPTIVE DISSORTATIVE MATING GENETIC
ALGORITHM
Carlos Fernandes1,2
J.J. Merelo1
Agostinho C. Rosa2
1
Department of Architecture and Computer Technology, University of Granada, Spain
2
L aSEEB-ISR-IST, Technical Univ. of Lisbon (IST), Portugal

2. SUMMARY
ADMGA
Non-Stationary Fitness Landscapes
Motivation
Replacement Strategies
Results
Conclusions and Future Work

3. Dissortative MatingDissortative Mating
 Mating between dissimilar individuals.
 Higher diversity.
Disruptive effect
High selective pressure + high disruption effect
parent
parent

4.  Chromosomes are alowed to crossover if and only
their Hamming Distance is above the threshold
value.
 The threshold self-adapts its initial value, and varies
during the run according to the population diversity
1111111111111111
1111111100001111
Hamming dist.: 4selection
ADMGA differs from the SGA at the recombination stage
4
the number of positions at which the
corresponding symbols are different
Adaptive Dissortative MatingAdaptive Dissortative Mating
GA (ADMGA)GA (ADMGA)

5. ADMGAADMGA
Population
New population = Offspring
population + best parents
Selects two and
computes h.d.
if h. d. > ts
if h. d. ≤ ts
Crossover and mutate
after n/2 (n is the population size)
Updates threshold
if (failed matings > successful matings) ts←
ts−1
else ts ← ts+1
5
diversity is controlling the threshold
population-wide elitism (or steady-state)

6. Stationary Fitness Functions:Stationary Fitness Functions:
Scalability with Trap FunctionsScalability with Trap Functions
order-2 (k = 2) order-3 order-4
6
non-deceptive nearly-deceptive fully deceptive
Scalability with problem size

7. Alternative Replacement StrategiesThreshold ValueThreshold Value
Initial threshold
value
n = 10,000; l = 10
n = 10; l = 10,000
n = 100
order-2

8. Dynamic OptimizationDynamic Optimization
ProblemsProblems
8

9. ADMGA: DynamicADMGA: Dynamic
Optimization ProblemsOptimization Problems
 Better performance on “slower”
dynamic problems
 The performance degrades as the
optimum moves faster
9

10. MotivationMotivation
 Improve ADMGA’s performance on
faster problems
 Is population-wide elitism a good or
bad strategy for fast dynamic
problems?
10

11. Replacement StrategiesReplacement Strategies
 RS 1: Original
 RS 2: Mutated copies of the old solutions
 RS 3: Mutated copies of the best solution
 RS 4: Random Immigrants (random solutions)
11

12. ADMGA: DynamicADMGA: Dynamic
Optimization ProblemsOptimization Problems
 Yang’s (2003) dynamic problem
generator:
• frequency of change (1/ε)
• severity (ρ)
12
 ε : 600, 1200, 2400, 4800, 9600, 19200, 38400
 ρ : random
 Offline performance: average of the best fitness throughout the run
 Statistical tests

13. TestsTests
 Several mutation probability and
population size values.
• mutation: dissortative mating affects optimal
probability
• population size: avoid extra computational effort
 binary tournament
 2-elitism
 uniform crossover (p=1.0)
• Balance disruptive effect and selective pressure
13

14. Results TestsTests
RS 1 vs GGA
RS 2 vs GGA
ε→ 600 1200 2400 4800 9600 19200 38400
onemax − − ≈ ≈ ≈ ≈ ≈
trap ≈ ≈ + + + + +
knapsack − − ≈ ≈ ≈ + +
ε→ 600 1200 2400 4800 9600 19200 38400
onemax − − − − ≈ ≈ ≈
trap − − − ≈ + + +
knapsack − − − − − ≈ +

15. Results TestsTests
RS 2 vs EIGA
ε→ 600 1200 2400 4800 9600 19200 38400
onemax − − − ≈ ≈ ≈ ≈
trap ≈ ≈ + + + + +
knapsack − − ≈ ≈ ≈ ≈ ≈

16. Genetic Diverstiy

17. Conclusions and Future Work
Mutating old solutions speeds up AMDGA on dynamic problems
Only two parameters need to be adjusted: population size and
mutation rate
ADMGA is at least competitive with EIGA
Performance according to severity
Constrained Dynamic Problems