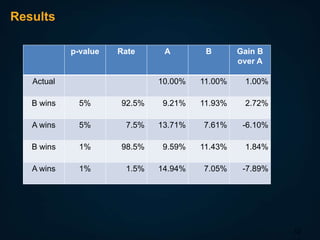
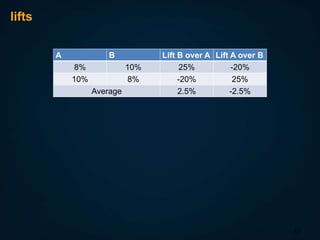
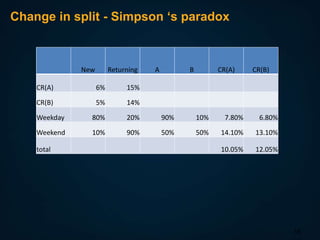
The document discusses A/B testing, specifically measuring the performance of multiple alternatives against a population to determine the best option, such as testing different web page layouts based on conversion rates. It highlights issues related to fairness, errors in test results, and the importance of maintaining independent observations. Additionally, it explores challenges in conducting tests, such as selection bias and how to control traffic allocation during tests.

1. A/B testing
Shlomo Lahav

2. The problem
Measuring the effect of multiple alternatives
on the performance over a given population.
2

3. Performance
A list of objective measurements
3

4. Possible solutions
• A model that describe the results and
evaluates the marginal effect of the
alternatives
• Test the alternatives side by side while all
the rest is equal
4

5. Example
• the problem: Testing two different layouts
of a web page (A and B)
•
•
•
•
Population: visitors/visits
Performance: conversion rate
Alternatives: two different layouts
Objective: the find the better layout and
asses the performance difference
5

6. What does it mean all the rest being equal
• Fairness: for every member in the
population, the probability to be allocated
to A is the same.
• For each member, any other decisions is
independent with the test allocation (A/B).
• Observations are independent
6

7. Population: Visitor vs. visit
Population
Visitor
Visitor
Visit
Measurement
Visit conversion
rate
Lifetime
conversions per
visitor
Visit conversion
rate
Issues
Independency is
violated
A visitor may be
exposed to both A
and B (in different
visits)
7

8. Errors
• When we compare a test alternative to the
control alternative
• False Positive – Calling the test to be the
winner by mistake
• False Negative – calling the control to be
the winner by mistake
8

9. When do we end the test
• After a predefined period/observations.
• When the difference is significant
9

10. What does it mean all the rest being equal
• Fairness: for every member in the
population, the probability to be allocated
to A is the same.
• For each member, any other decisions is
independent with the test allocation (A/B).
• Observations are independent
10

11. Example
• We want to test two alternatives and
select the better one.
• The results are: CR(A)=9.21%,
CR(B)=11.93%. The win of B is statistical
significant (p-value<5%).
• We need to estimate the gain of B vs. A.
• Is our estimate of 2.72% a fair estimate?
11

12. Results
p-value
Rate
Actual
A
B
Gain B
over A
10.00%
11.00%
1.00%
B wins
5%
92.5%
9.21%
11.93%
2.72%
A wins
5%
7.5%
13.71%
7.61%
-6.10%
B wins
1%
98.5%
9.59%
11.43%
1.84%
A wins
1%
1.5%
14.94%
7.05%
-7.89%
12

13. Selection bias
• An AB test is conducted between A1,
A2,…,An
• After the test is completed, we select Ak.
• Should we expect Ak to perform as it did
during the test?
• Does the test outcome (the rank of k)
affects our expectation?
13

14. What else can go wrong?
• Independency is not maintained (traffic,
changes etc.)
• The fairness is handled by random
allocation. This can be biased due chance
• The significance level is usually higher
than planned (continues evaluation) which
results in a higher false positive.
14

15. How to control the traffic split?
• By percentage or round robin?
• Can we change the split?
15

16. Another example
• Need to test two design layouts in multiple
location, while each location has a
different conversion rate.
• Different populations – use lifts and
accumulate the lifts.
• How do we calculate the lift: A over B or B
over A?
16

17. lifts
A
B
8%
10%
10%
8%
Average
Lift B over A Lift A over B
25%
-20%
-20%
25%
2.5%
-2.5%
17

18. Change in split - Simpson ‘s paradox
New
Returning
A
B
CR(A)
CR(B)
CR(A)
6%
15%
CR(B)
5%
14%
Weekday
80%
20%
90%
10%
7.80%
6.80%
Weekend
10%
90%
50%
50%
14.10%
13.10%
10.05%
12.05%
total
18

19. Can we remove alternatives
• Start with 3 alternatives (equal split)
• Remove one
start
0
0
0.5
0.5
1
1
modify
0
0
0
1
1
1
19

20. Multiple tests
• Is it valid to run multiple AB tests
simultaneously?
20