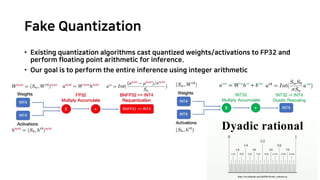
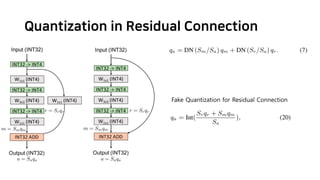
- New quantization algorithm called HAWQ-V3 that uses only integer multiplication, addition, and bit shifting for inference, with no floating point operations or integer division - Achieves higher accuracy than prior work, including up to 5% higher than Google's integer-only method, with no accuracy degradation for INT8 quantization - Proposes a novel ILP formulation to find optimal mixed precision of INT4 and INT8 that balances model size, latency, and accuracy - Implementation in TVM demonstrates up to 1.5x speedup for INT4 quantization compared to INT8 on Nvidia T4 GPU tensor cores

1. HAWQ-V3: Dyadic Neural Network
Quantization
Zhewei Yao, Zhen Dong, Zhangcheng Zheng, Amir Gholami, Jiali Yu, Eric Tan, Leyuan Wang,
Qijing Huang, Yida Wang, Michael W. Mahoney, Kurt Keutzer
UC Berkeley, ICML 2021
Presenter: Jemin Lee
https://leejaymin.github.io/index.html
14 Oct. 2021
DL Compiler Study Season #1

2. Summary
• New integer only quantization algorithm with only INT
multiplication, addition, and bit shifting
• No FP32 arithmetic and not even integer division for the entire
inference
• No accuracy degradation for INT8 (up to 5% higher than prior
SOTA from Google)
• Novel ILP formulation for mixed-precision INT4/INT8
quantization
• Optimal trade-offs between model size, latency, and accuracy

3. Summary (cont.)
• Direct hardware implementation and verification
• First implementation of INT4 and mixed-precision quantization in TVM
• Up to 1.5x speed up with INT4 compared to INT8 quantization

4. Fake Quantization
• Existing quantization algorithms cast quantized weights/activations to FP32 and
perform floating point arithmetic for inference.
• Our goal is to perform the entire inference using integer arithmetic

5. Division Cost

6. Batch Normalization Fusion for
Quantization
• Quantizing the BN parameters often leads to significant
accuracy degradation
• Many prior works keep BN in FP32 precision
• The scaling factor of !
𝒃 is enforced to be 𝑺!
𝒃= 𝑺𝒉𝑺!
𝒘
• Possible to directly add

7. Quantization in Residual Connection
Fake Quantization for Residual Connection

8. Mixed Precision and Integer Liner
Programming
Integer Linear Programming (ILP) problem
Search space: 𝐵!
• 𝐵 choices for quantizing each layer:
INT4 or INT8
• 𝐿 layers
Assume the perturbations for each layer ar
e independent of each other [1,2].
• Ω = ∑"#$
!
Ω"
(&!)
• The i-th layer’s perturbation with b_i bit
[1] ICCV2019, HAWQ
[2] NeurIPS 2020, HAWQ-V2

9. Mixed Precision and Integer Liner
Programming(cont)
• Find the right bit precision and fit the following contains.
• ILP solver (PULP library) takes 1 second given the sensitivity metric.
• RL based method (SongHan, HAQ) takes tens of hours.

10. Mixed Precision and Integer Liner
Programming(cont)
[1] ICCV2019, HAWQ
[2] NeurIPS 2020, HAWQ-V2

11. Hardware Deployment
• Direct measurement is always good metric
• FLOPs, model size could lead wrong results
• Turing Tensor Cores of T4 GPU support INT4, INT8
• There is no compiler to map a NN quantized int4 to tensor
cores using WMMA instructions
• Integration with TVM
• TVM 0.6
• Graph level implementation for INT4: memory planning, constant
folding, and operator fusion
• New scheduler for Tensor Cores in auto-tuner of TVM
• Set the knobs: thread size, block size, loop ordering

12. Results
• HAWQv3 achieves higher accuracy than the integer-only work [google, CVPR18]
• Uniform 4bit Quant is the first outcome reported in the literature
• Distillation helps most for mixed-precision quantization except uniform ones
• Comparable accuracy to prior methods that use non-standard bit precision and FP32
operation (PACT, RVQuant, OneBitwidth, HAQ)

13. Results (cont.)
• The correlation between model size and BOPS is weak
• The model size does not correlate with accuracy
• All the results are from the real measurement and are not simulated

14. Appendix I: ILP

15. Demo

16. Demo
./mixed_precision_models/tuning_logs/resnet50_HWNC_mixed_batch_8.log
...
…

17. Conclusion
• A new low precision integer-only quantization framework.
• Executed with only integer Mul., Add., and Bit-shift
• Hardware-aware ILP considers optimal trade-off:
• perturbation(accuracy) and model size, inference speed, and total BOPS
• Solved very efficiently, under a second
• Results for uniform and mixed-precision INT4/8
• implemented by extending TVM (INT4, INT4/8 on T4 GPU)
• Verified all the results, by matching the activation of each layer with our PyTorch
• Machine precision and final accuracy of the model
• The framework, the TVM implementation, and the quantized models have been open
sourced: https://github.com/zhen-dong/hawq