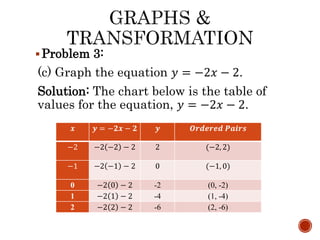
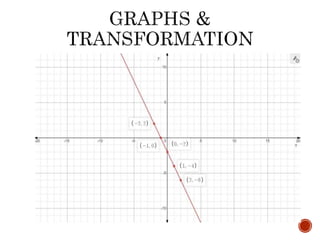
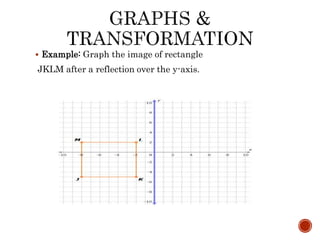
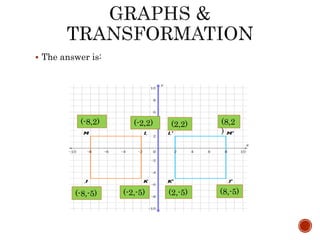
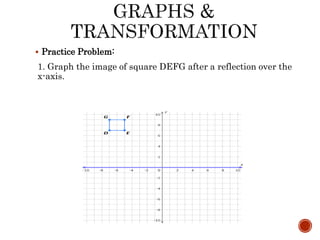
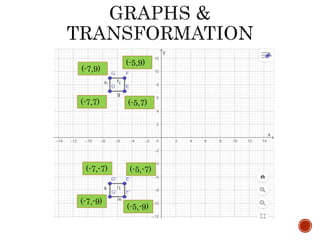
The document outlines a lesson on the concept of reflection across an axis, including explanations, rules for reflecting points across the x-axis and y-axis, and provides practice problems with solutions. Specific examples, such as graphing the reflection of a rectangle and a square, illustrate these principles. Students are instructed to complete classwork from handouts, including specific problems related to reflecting equations and figures.

1. Subject Teacher: Suraiya Hossain

2. Day: Thursday Date: 02/05/2024
Classwork:
Concept of reflection across an axis will be explained.
From handout,
Questions- 3(c), example 1 and practice problem 1 of reflection
will be done in the class.

3. Problem 3:
(c) Graph the equation 𝑦 = −2𝑥 − 2.
Solution: The chart below is the table of
values for the equation, 𝑦 = −2𝑥 − 2.
𝒙 𝒚 = −𝟐𝒙 − 𝟐 𝒚 𝑶𝒓𝒅𝒆𝒓𝒆𝒅 𝑷𝒂𝒊𝒓𝒔
−2 −2 −2 − 2 2 (−2, 2)
−1 −2 −1 − 2 0 (−1, 0)
0 −2 0 − 2 -2 (0, -2)
1 −2 1 − 2 -4 (1, -4)
2 −2 2 − 2 -6 (2, -6)

5.  Reflection:
A reflection flips a figure over a line to create a mirror image.
 Rules for performing a reflection across an axis
1. When reflecting across the y-axis, the y-coordinate remains
the same and the x-coordinate changes sign. For example,
(2,3) becomes (-2, 3) after reflection through y-axis.

6. 2. When reflecting across the x-axis, the x-coordinate remains
the same and the y-coordinate changes sign.
For example, (2, 3) becomes (2, -3) after reflection across the x-
axis.

7.  Example: Graph the image of rectangle
JKLM after a reflection over the y-axis.

8. Solution: The coordinates in the rectangle JKLM are:
J (-8, -5), K(-2, -5), L(-2, 2) and M(-8, 2).
So after reflection across the y-axis, the coordinates of new
points will be
J’(8, -5), K’(2, -5), L’(2, 2) and M’(8, 2).

9.  The answer is:
(-2,2)
(-8,2)
(-8,-5) (-2,-5)
(2,2) (8,2
)
(2,-5) (8,-5)

10.  Practice Problem:
1. Graph the image of square DEFG after a reflection over the
x-axis.

11. Solution: The coordinates in the square DEFG are:
D (-7, 7), E(-5, 7), F(-5, 9) and G(-7, 9).
So after reflection across the x-axis, the coordinates of new
points will be
D’(-7, -7), E’(-5, -7), F’(-5, -9) and G’(-7, -9).

12. (-5,7)
(-7,7)
(-5,9)
(-7,9)
(-5,-7)
(-7,-7)
(-5,-9)
(-7,-9)