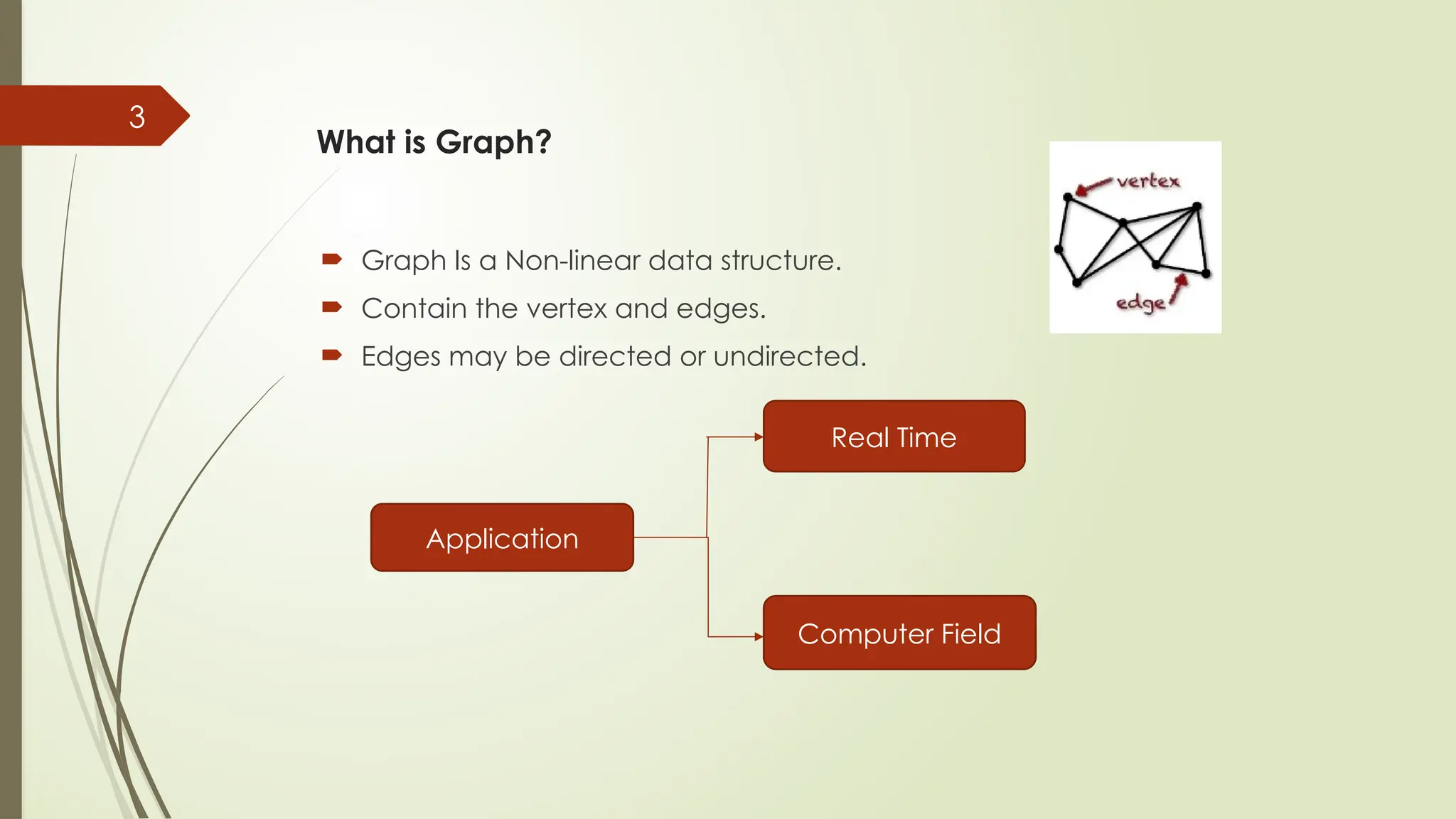
✨ Unlock the Power of Connections: Graph Theory is EVERYWHERE! ✨ Think math is just equations? Think again! This deck reveals how Graph Theory—the science of networks—is the secret engine behind Google Maps, social media, and even the phone in your pocket. 🤯 🔮 What You’ll Discover: The Core Concept 🧠: What is a graph? It's simpler than you think: just vertices (points) and edges (lines connecting them). This simple idea powers the modern world. 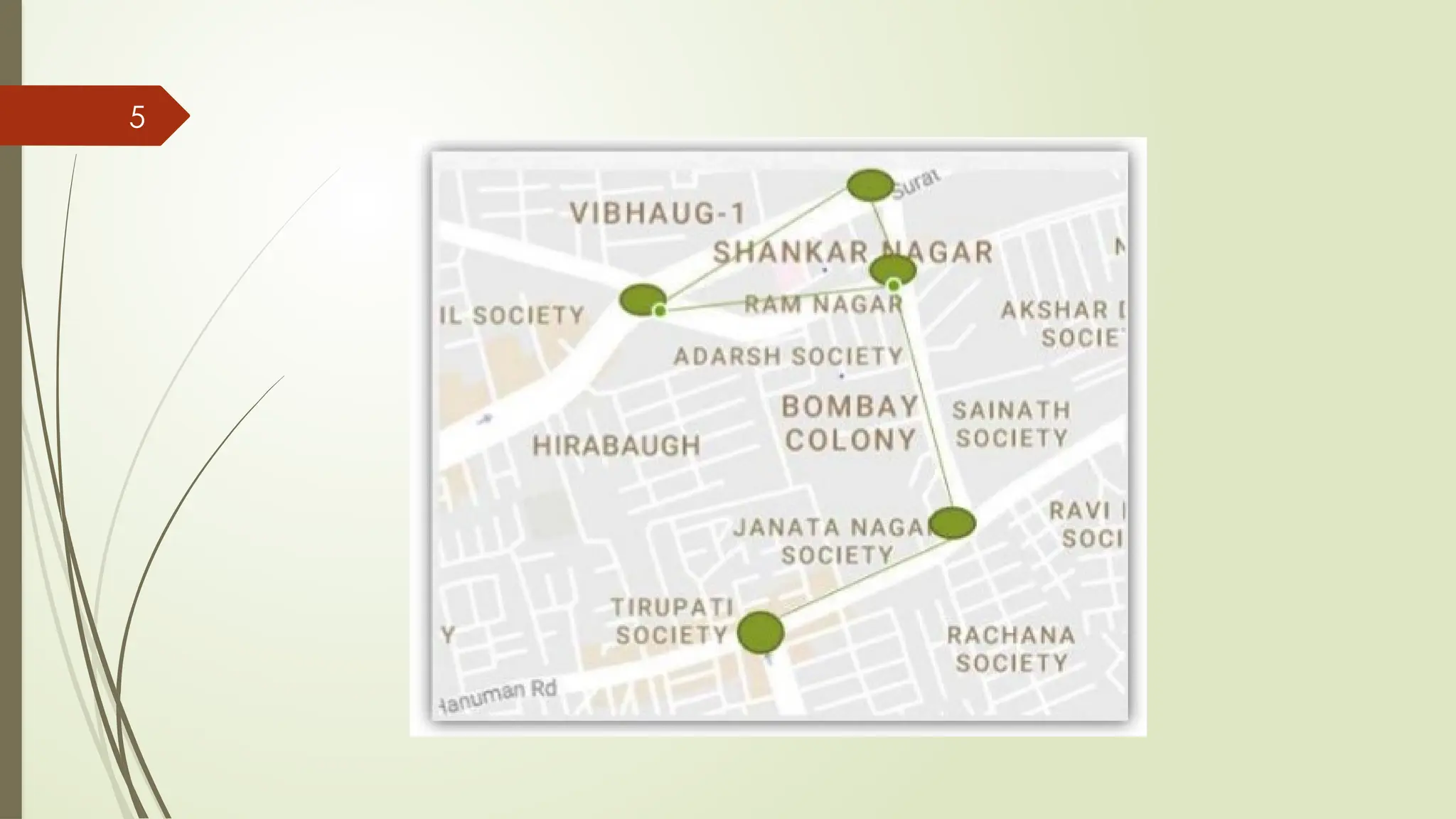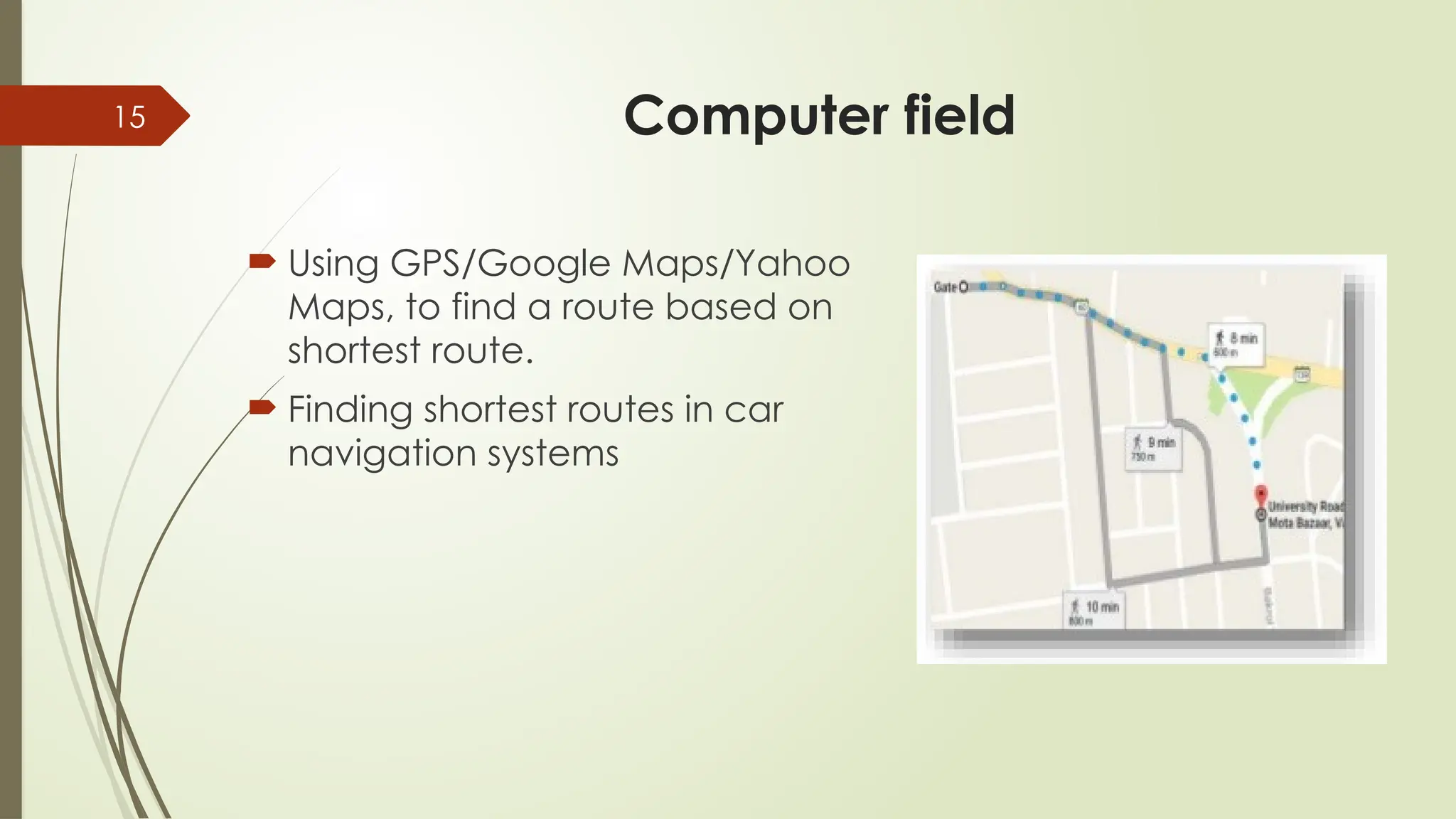Real-World Magic 🌍: See mind-blowing applications you use daily: Google Maps: Finds the shortest path because roads are edges and intersections are vertices! Social Networks: You are a vertex! Every friend is a connection (edge). Facebook & Instagram run on a giant graph. The Internet: How Google ranks websites using the "web graph" of hyperlinks. 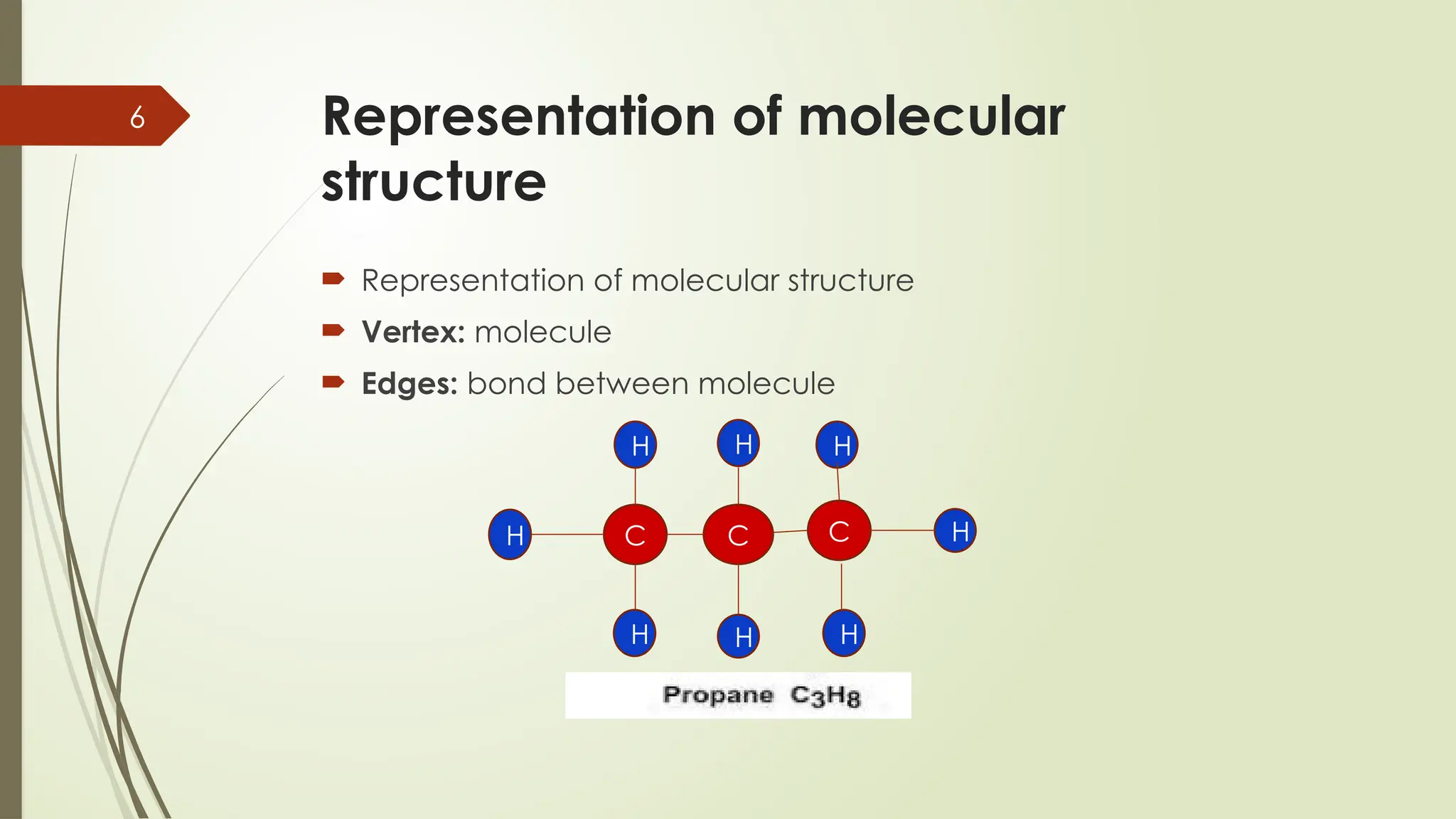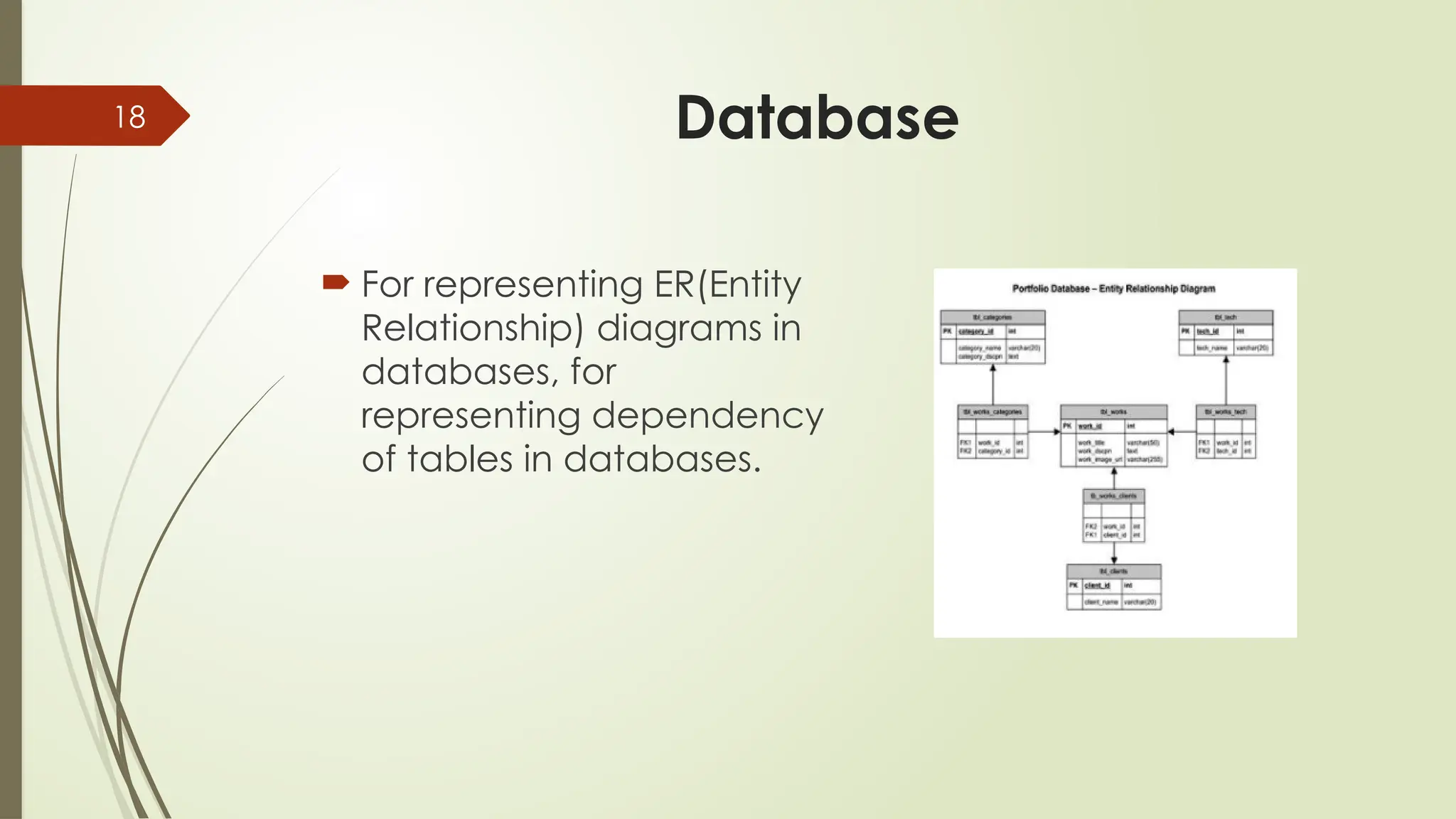Chip Design: Optimizing millions of transistor connections inside your computer's CPU. Visual Learning 🎨: Complex ideas are broken down with clear examples and intuitive visuals. No heavy math, just clear logic. Key Problems Solved ⚙️: The Shortest Path problem (getting from A to B fastest). The Travelling Salesman problem (the most efficient tour). 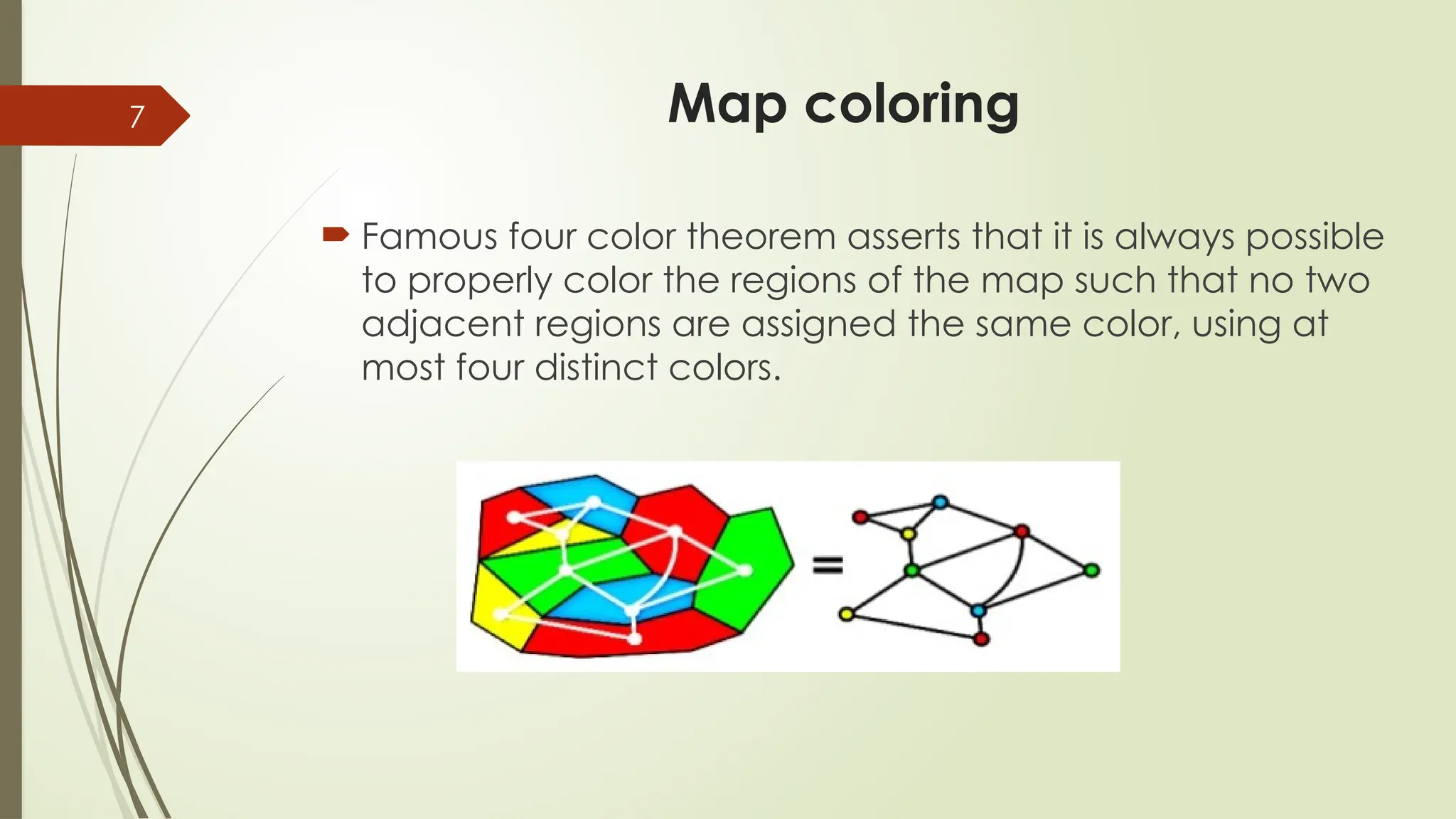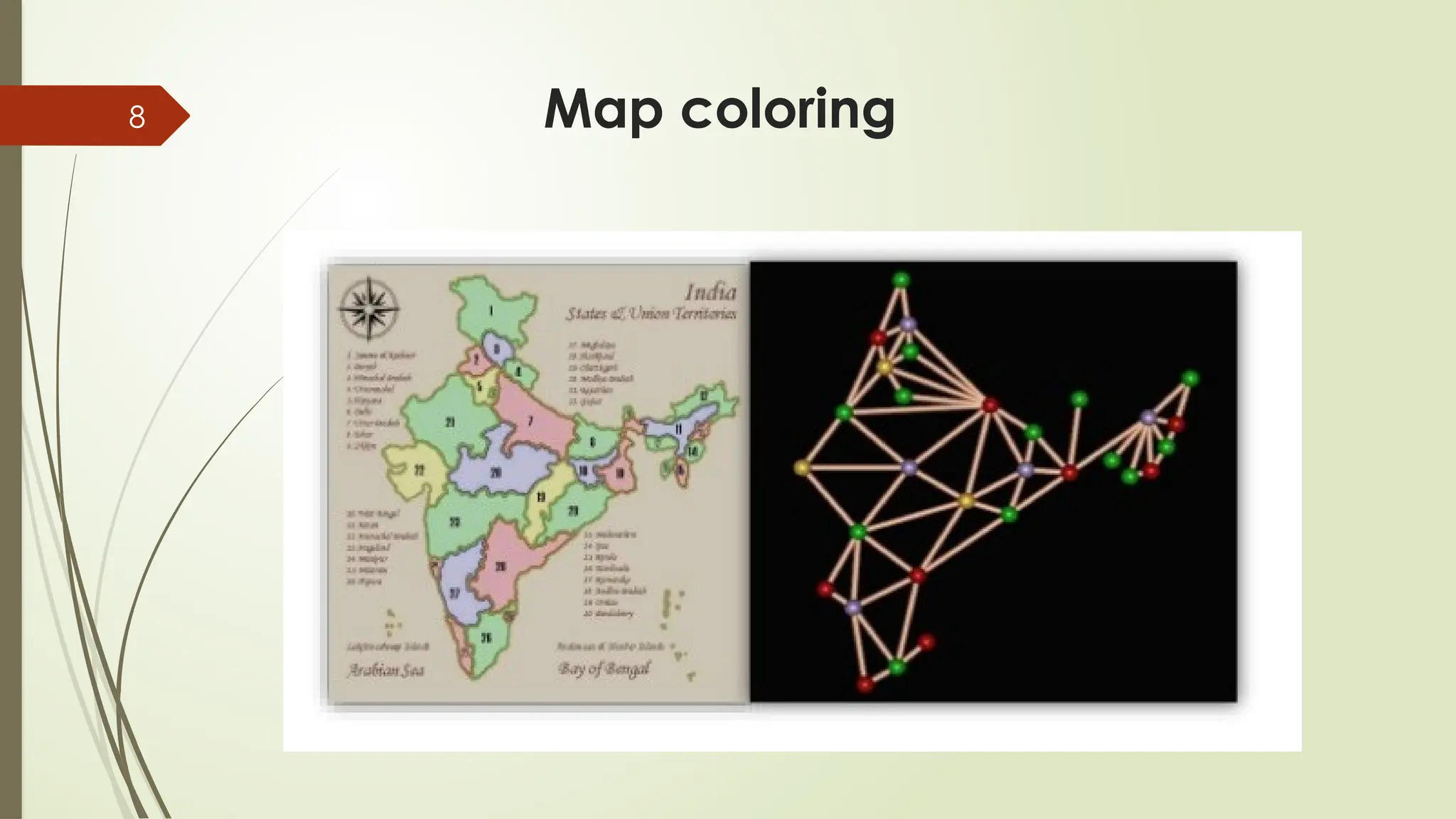The Map Coloring theorem (how to color any map with no same-colored neighbors). Pro Tip 💡: The #1 thing to remember? Graphs are about relationships, not just things. Master that, and you'll see networks everywhere! 💬 Key Quotes to Remember: "Graph theory is the language of networks." "From social media to silicon chips, everything is connected." 🚀 Ready to See the World Differently? ✅ SAVE this guide to finally get how tech really works! ✅ TAG your study buddy or tech-loving friend! #GraphTheory #ComputerScience #Tech ✅ FOLLOW for more content that turns complex topics into simple superpowers! 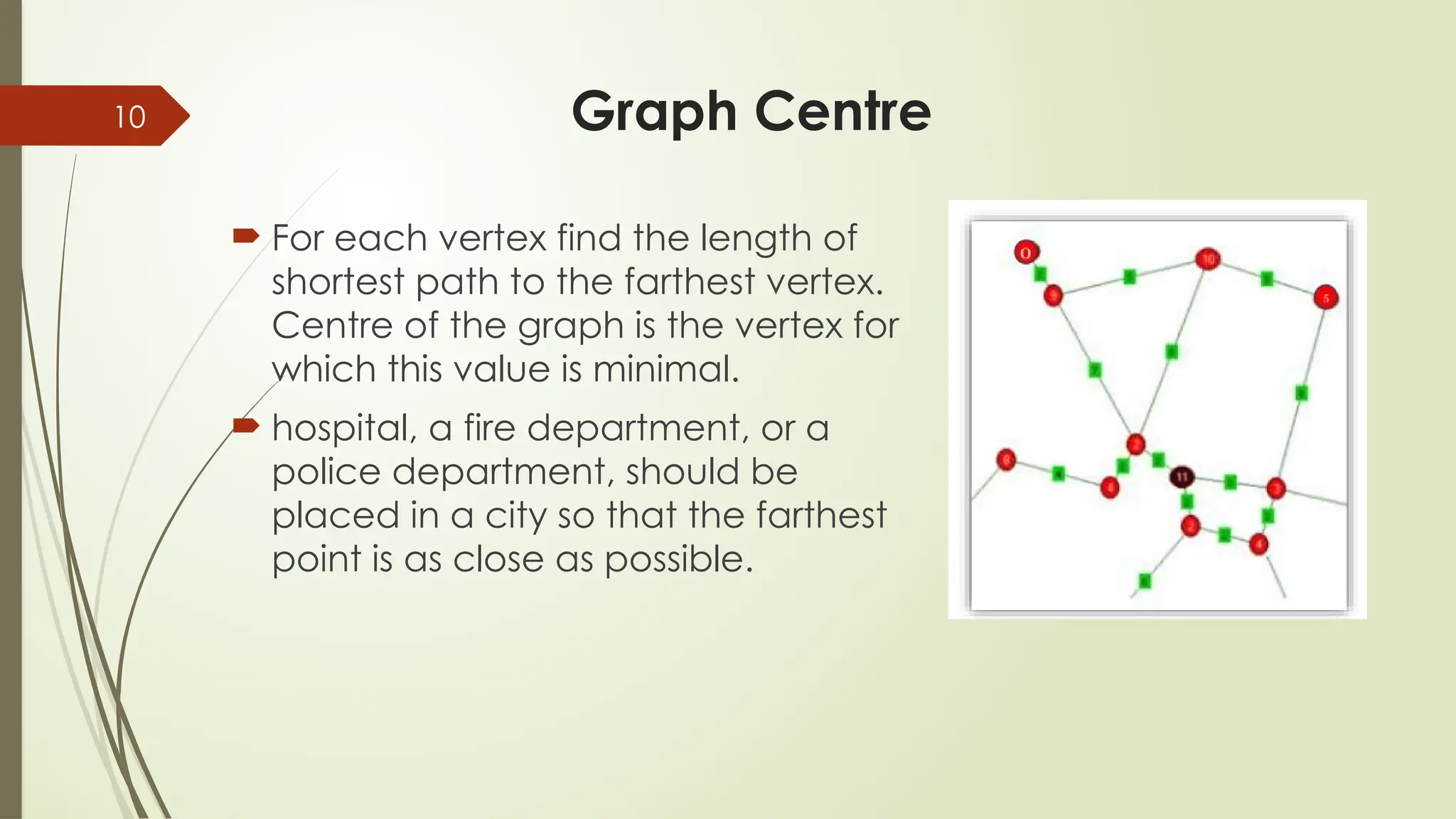📌 BONUS: The slides reveal how a simple graph center algorithm decides the optimal spot for a new hospital or fire station in a city! 🚒

1. 1
Applications of
Graph Theory
Made by: Zel-e-Huma

2. 2 Contents
 What is Graph?
 Applications
 Real time applications
 Computer Field applications

3. 3
What is Graph?
 Graph Is a Non-linear data structure.
 Contain the vertex and edges.
 Edges may be directed or undirected.
Application
Real Time
Computer Field

4. 4
REAL TIME
 Transportation networks
Vertices: In road networks vertices are intersections.
Edges : Road segments between intersection.
 Used by
Google maps, Bing maps and now Apple IOS 9 maps for map
programs.

5. 5

6. 6 Representation of molecular
structure
 Representation of molecular structure
 Vertex: molecule
 Edges: bond between molecule
C C C H
H
H
H
H
H
H
H

7. 7 Map coloring
 Famous four color theorem asserts that it is always possible
to properly color the regions of the map such that no two
adjacent regions are assigned the same color, using at
most four distinct colors.

8. 8 Map coloring

9. 9 Three cottage problem
 The three cottage problem is a
well-known mathematical puzzle.
It can be stated like this:
 Three cottages on a plane (or
sphere) and each needs to be
connected to the gas, water, and
electric companies.
 Planar Graph

10. 10 Graph Centre
 For each vertex find the length of
shortest path to the farthest vertex.
Centre of the graph is the vertex for
which this value is minimal.
 hospital, a fire department, or a
police department, should be
placed in a city so that the farthest
point is as close as possible.

11. 11 Shortest Path
 Consider some communications stations (for telephony,
cable television, Internet etc.) and a list of possible
connections between them, having different costs.
 Find the cheapest way to connect these stations in a
network. This may be used for example to connect
villages to cable television, or to Internet.
 The same problem, but instead of connecting
communications stations - villages are to be connected
with roads.

12. 12 Travelling Salesman Problem
 A salesman has to visit a number
of cities to deliver items. What is
the shortest route that connects
all the cities?

13. 13 Airline Network
 Graph theory is already utilized in flight
networks.
 Airlines want to connect countless cities
in the most efficient way, moving the
most passengers with the fewest
possible trips

14. 14 Minimizing connection in IC
 Integrated circuits (ICs) consist of
millions of transistors which need to be
connected.
 It is important to optimize these
countless connections to improve the
performance of the chip

15. 15 Computer field
 Using GPS/Google Maps/Yahoo
Maps, to find a route based on
shortest route.
 Finding shortest routes in car
navigation systems

16. 16 Computer network
 Graph theory used in all types of
topology for configure network.
 Vertex :each device (Router, pc,
etc..)
 Edges: connection between the
devices.

17. 17
Digital Graph
 Document link graphs. The best known example is
the link graph of the web,
 Vertex: web page, directed edge: hyperlink
 Google any page that is very good will have
many other pages linking to it. Pages that are
rarely visited, or not very interesting, will be very
“lonely” in the internet graph
 This gives a way to rank websites and allows
Google to display the best results at the
beginning.

18. 18 Database
 For representing ER(Entity
Relationship) diagrams in
databases, for
representing dependency
of tables in databases.

19. 19 Social Network
 Connecting with friends on social
media, where each user is a
vertex, and when users connect
they create an edge.
 Facebook,Twiter,Instagram etc…

20. 20
ANY QUESTION

21. 21
THANK YOU