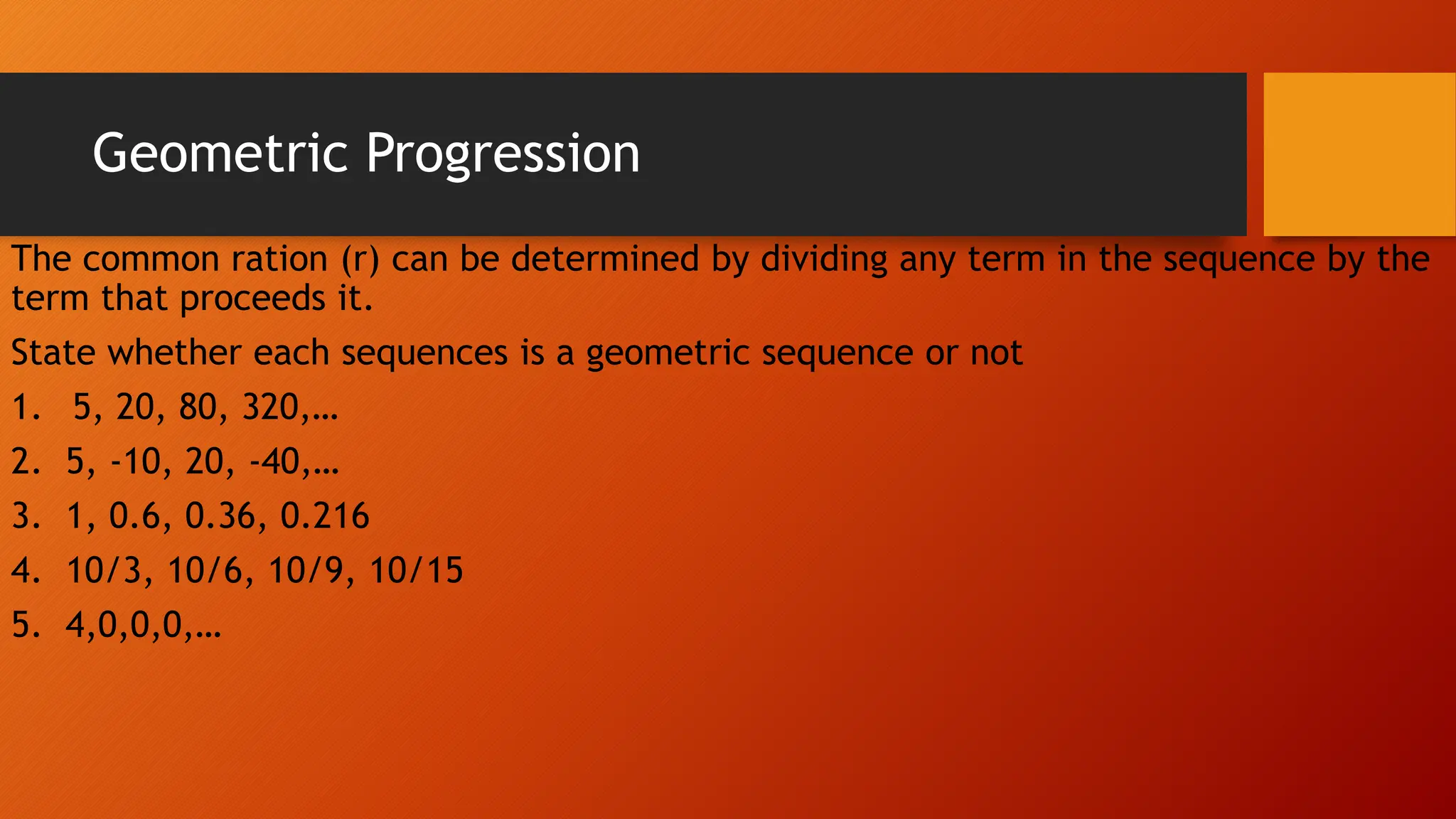
A geometric progression is a sequence where each term is obtained by multiplying or dividing the preceding term by a fixed number called the common ratio. If the pattern of numbers is increasing, the common ratio is multiplied; if decreasing, the common ratio is divided. The common ratio can be found by dividing any term by the one before it. Formulas are provided to find a specific term, insert terms, or calculate the sum of a geometric progression. Examples are worked through applying the formulas.

1. Geometric Progression

2. Geometric Progression
- It is a sequence where each term after the first term is
obtained by multiplying and dividing a fixed number called the
“common ratio(r)” to the preceding number in order to obtain
the succeeding number.
- When the pattern of numbers have an increasing trend then the
common ratio is multiplied to the preceding number
- If the trend is decreasing, then the common ratio is divided to
the preceding number.
• When the pattern or trend of numbers is increasing the
operation involved is multiplication otherwise if the trend is
decreasing then the operation involved is division.

3. Geometric Progression
The common ration (r) can be determined by dividing any term in the sequence by the
term that proceeds it.
State whether each sequences is a geometric sequence or not
1. 5, 20, 80, 320,…
2. 5, -10, 20, -40,…
3. 1, 0.6, 0.36, 0.216
4. 10/3, 10/6, 10/9, 10/15
5. 4,0,0,0,…

4. Geometric Progression
Find the missing terms in each geometric sequence
1. 3, 12, 48, ____, _____
2. 32, 64, 128, _____,_____
3. 120, 60, 30,_____,______
4. 5, ____, 20, 40, _____
5. 5x2, ____, 5x6, 5x8, _____

5. Geometric Progression
Formula in finding the nth term of geometric sequence
Ln= a(r)n-1
Example 1.Given the Geometric Progression (GP) as shown 2 , 4 , 8 , 16 , 32 …
a) What is the 16th term ?
b) What is the 23rd term ?
c. What is the 12th term ?

6. Geometric Progression
Formula in finding the nth term of geometric sequence
Ln= a(r)n-1
Example 2.Given the Geometric Sequence 3,9,27…
a) What is the 15th term ?
b) What is the 20th term?
c) What is the 37th term?

7. Geometric Progression
Formula in inserting geometric means
Ln= a(r)n-1
Example 1. Insert three geometric means between 3 and 243

8. Geometric Progression
Formula in inserting geometric means
Ln= a(r)n-1
Example 2. Insert 4 geometric means between 2 and 64

9. Geometric Progression
Formula in inserting geometric means
Ln= a(r)n-1
Example 3. Insert 3 geometric means between 256 and 16

10. Geometric Progression
Formula in finding the sum of geometric sequence
Sn = a(1-rn) r≠1
1-r
Ex.1. Find the sum of the first 5 terms of the geometric sequence 3,6,12,…?

11. Geometric Progression
Formula in finding the sum of geometric sequence
Sn = a(1-rn) r≠1
1-r
Ex.2. What is the sum of the first 15 terms of the sequence -16,-32,-64,…?