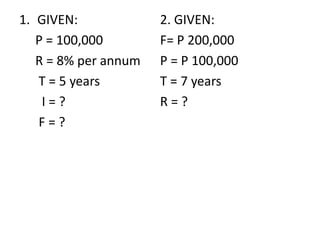This document discusses the mathematics of finance, including simple and compound interest calculations. Simple interest is calculated as Interest = Principal x Rate x Time. Compound interest calculates interest on prior interest amounts over multiple compounding periods. Formulas are provided to calculate interest, principal, maturity/final amounts, and rates for both simple and compound interest scenarios. Examples demonstrate applying the formulas to solve for unknown values.

1. MATHEMATICS OF FINANCE
INTEREST:
> Is a fraction or percentage being imputed to a sum of
money.
SIMPLE INTEREST:
> Is essentially the interest charged to a borrower or
earned by a lender for the full term of the loan.

2. • FORMULA:
I = P x R x T
Where:
I = interest
P = Principal
R = Rate
T = time

3. • TIME CONVERSION:
• > IF THE TIME IS IN TERMS OF:
• MONTHS, DIVIDE BY 12.
• SEMIANNUALLY, DIVIDE BY 2.
• QUARTERLY, DIVIDE BY 4.
• SEMIMONTHLY, DIVIDE BY 24.
• > IF THE TIME IS EXPRESSED IN DAYS:
• EXACT INTEREST: t = number of days/ 365
• ORDINARY INTEREST: t =number of days/ 360

4. PRINCIPAL : The sum of money that
someone borrows.
RATE : is a percentage of the principal
amount.
TIME: is the agreed date or period when the
loan will be paid in full.

5. • 1. Given:
• P = P10,000
• R= 5 % per month
• Time = 5 months
• I = ?
• 2. Given:
• I = P 6,000
• P = P 20,000
• R = 8% per year
• T = ?
3. Given:
R = 15% per month
Time = 6 months
I = P 4,500
P = ?
4. Given:
P = P 30,000.
I = P 9,000.
R = ? ( per month)
T = 3 months

6. MATURITY AMOUNT OR FINAL
AMOUNT: ( for simple interest)
Is the amount to be paid to the holder of a
financial obligation at the obligation’s
maturity.
FINAL AMOUNT FORMULA:
F = P + I
or
F = P ( 1 + rt) r = F – P/ Pt
t = F –P/ Pr

7. 1. GIVEN:
P = 100,000
R = 8% per annum
T = 5 years
I = ?
F = ?
2. GIVEN:
F= P 200,000
P = P 100,000
T = 7 years
R = ?

8. COMPOUND INTEREST:
Is similar to simple interest, only
that the interest charged or
earned is being rolled – up and
reinvested with the principal
amount.
The sum by which the original
principal has increased by the end
of the term of the investment.

9. The conversion period it can be:
• Quarterly ( 4 periods)
• Semiannually( 2 periods)
• Monthly ( 12 months)

10. FORMULA:
n
F = P( 1 + i)
Where:
F=Maturity amount
P = Principal amount
i = Interest rate per conversion( expressed as decimal )
i = j / m j : annual rate , m = number of conversion
periods per year
n= number of conversion periods

11. • Example 1.
Accumulate P 5,000 for 3 years at 10%
compounded quarterly.
Given:
P = P5,000
n=3(4) = 12
i = j/m = 10%/ 4 = .10/4 = 0.025

12. • Example 2
• Find the amount due at the end of 6 ¾ years
if P 2,000 is invested at 12% compounded
monthly.
• Given:
• i=j /m = .12/ 12 = .01
• P = p2,000
• n=12(6 ¾) =81

13. • MATURITY AMOUNT in Compound amount
• Formula:
-n
M = F ( 1 + I ) or
F
=
n
( 1 + i)
Where:
M = Maturity amount

14. • 1. Find the maturity amount of p5,000 due in
6 years if money is worth 12% compounded
semiannually.
• 2. If money can be invested at 12%
compounded semiannually, find the maturity
amount of p1,000 due at the end of 5 ½
years.