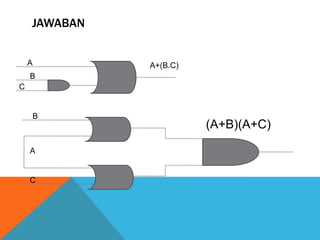
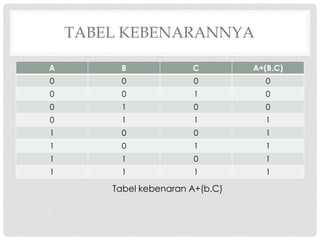
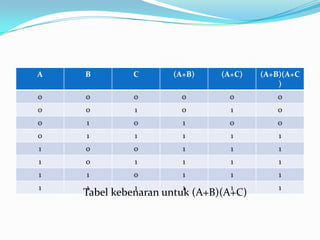
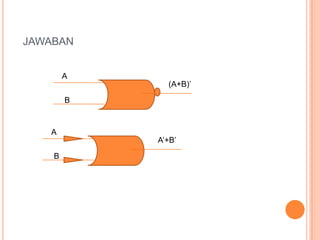
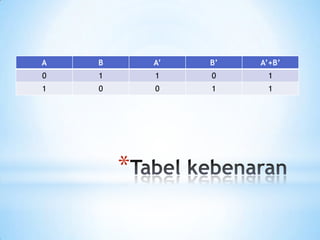
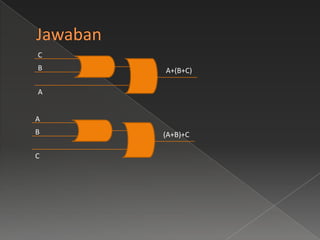
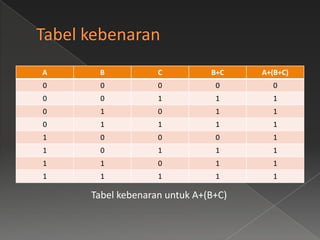
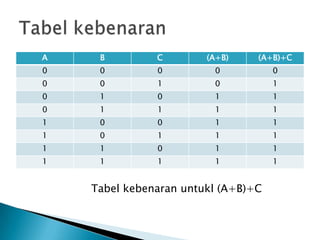
Dokumen ini membahas hukum distributif, hukum De Morgan, dan hukum asosiasi dalam aljabar boolean, serta memberikan contoh soal dan tabel kebenarannya. Penjelasan di dalamnya mencakup penggunaan variabel dan operasi logika dalam berbagai bentuk persamaan. Hukum-hukum ini digunakan untuk menyelesaikan masalah dalam aljabar boolean.

1. Persentation sistem digital
Nama: Genanda
S1/TI/2A/P

2. Hukum ditributif
Hukum komutasi pada prisipnya adalah adanya
pembagian (pengelompokan) variable dalam satu
persamaan aljabar boolean.
Soal
A+(B.C)=(A+B)(A+C)
(A+B)(A+C)

3. JAWABAN
A A+(B.C)
B
C
B
(A+B)(A+C)
A
C

4. TABEL KEBENARANNYA
A B C A+(B.C)
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Tabel kebenaran A+(b.C)

5. A B C (A+B) (A+C) (A+B)(A+C
)
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 1 0 0
0 1 1 1 1 1
1 0 0 1 1 1
1 0 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
Tabel kebenaran untuk (A+B)(A+C)

6. Hukum De Morgan ( diambil dari nama seorang
matematik dari inggris 1806-1871)
merupakan pengembangan dari aljabar
boole, yaitu menyelesaikan berbagai masalah
dalam aljabar boole dengan menggunakan
negasi NAND atau NOR.
Soal
(A+B)’=A’+b’

7. JAWABAN
A
(A+B)’
B
A
A’+B’
B

8. A B (A+B)’
0 1 0
1 0 0
Tabel kebenaran untuk (A+B)’

9. A B A’ B’ A’+B’
0 1 1 0 1
1 0 0 1 1
*

10. Hukum asosiasi pada prisipnya adalah adanya
hubungan keterikatan antara variable dalam
satu persamaan aljabar boole, hukum ini
berlaku untuk gerbang AND
Soal
A+(B+C)=(A+B)+C
*

11. C
B A+(B+C)
A
A
B (A+B)+C
C

12. A B C B+C A+(B+C)
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 1 1
1 0 0 0 1
1 0 1 1 1
1 1 0 1 1
1 1 1 1 1
Tabel kebenaran untuk A+(B+C)

13. A B C (A+B) (A+B)+C
0 0 0 0 0
0 0 1 0 1
0 1 0 1 1
0 1 1 1 1
1 0 0 1 1
1 0 1 1 1
1 1 0 1 1
1 1 1 1 1
Tabel kebenaran untukl (A+B)+C

14. selesai