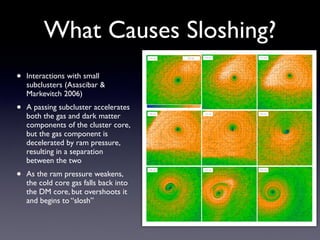
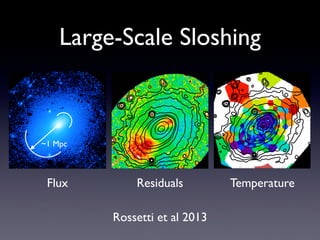
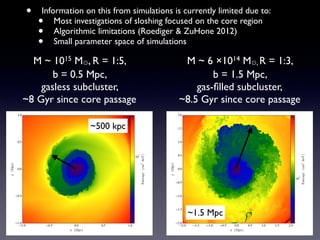
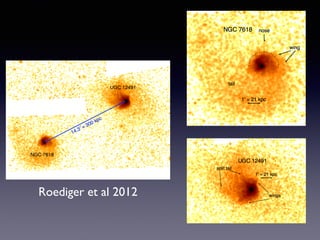
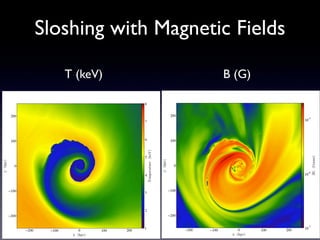
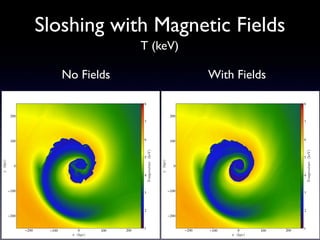
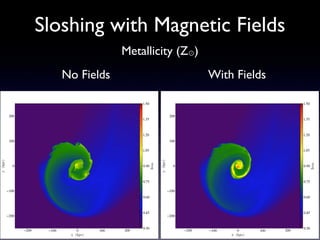
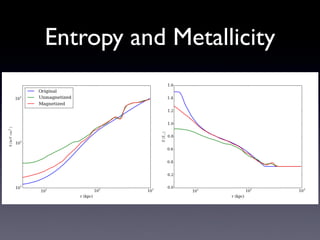
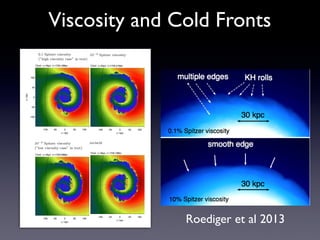
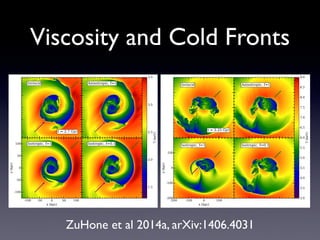
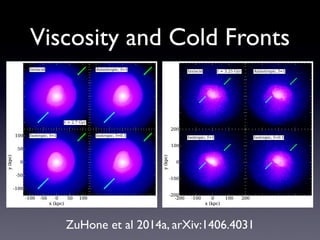
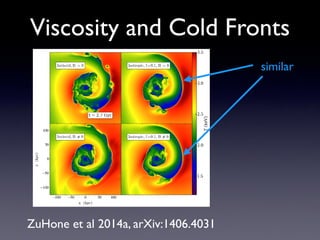
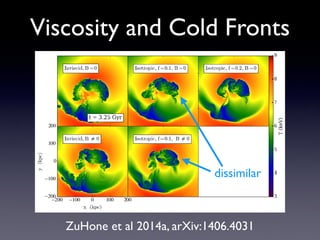
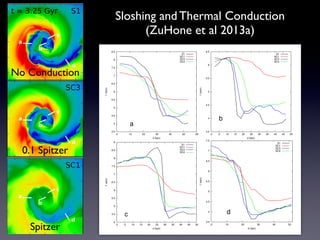
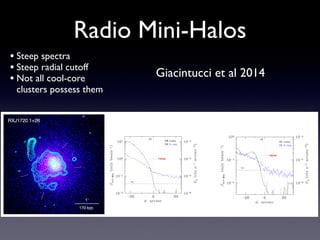
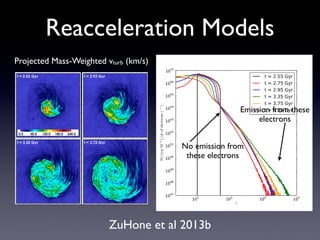
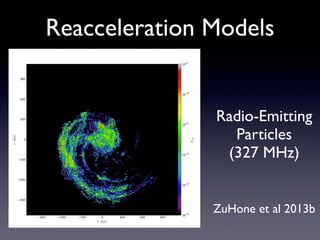
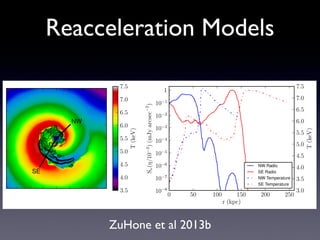
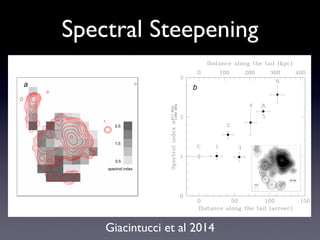
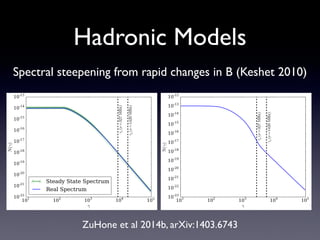
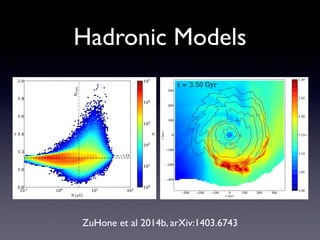
The document discusses gas sloshing in galaxy clusters, particularly the observation of cold fronts and the dynamics involved in their formation. It highlights the mechanisms causing sloshing, such as interactions with subclusters, and addresses the role of viscosity, magnetic fields, and thermal conduction in stabilizing cold fronts. Furthermore, it raises several open questions regarding the formation of large-scale fronts and the origins of radio mini-halos in relation to particle acceleration and spectral steepening.

1. Gas Sloshing: Simulations
and Observations
John ZuHone (NASA/GSFC, Maryland)
A2319

2. Gas Sloshing?
• The signature: cold fronts in
relaxed cool-core clusters
• Spiral-shaped discontinuities
in surface brightness and
projected temperature
• Most easily explained by the
“sloshing” of the cool core
gas in the dark matter
potential well
• Cold gas has been uplifted
from the gravitational
potential minimum and
formed a contact discontinuity
in pressure equilibrium with
the hotter, less dense gas
Markevitch &Vikhlinin 2007

3. What Causes Sloshing?
• Interactions with small
subclusters (Asascibar &
Markevitch 2006)
• A passing subcluster accelerates
both the gas and dark matter
components of the cluster core,
but the gas component is
decelerated by ram pressure,
resulting in a separation
between the two
• As the ram pressure weakens,
the cold core gas falls back into
the DM core, but overshoots it
and begins to “slosh”
4 ASCASIBAR AND MARKEVITCH
FIG. 3.— Evolution of the cold front induced by a purely dark matter satellite. Parameters of the encounter are R = 5 and b = 500 kpc; the pericenter distance
at the first core passage (which occurs at 1.37 Gyr) is ∼ 150 kpc. Color maps show the gas temperature (in keV) in a slice in the orbital plane. The temperature
scale shown in the top left panel (in keV) is the same for all panels. Arrows represent the gas velocity field w.r.t. the main dark matter density peak (for clarity
the velocity scale is linear at low values, then saturates). Contours are drawn at increments of a factor of 2 in the local dark matter density. The white cross shows
the center of mass for the main cluster DM particles (not for the whole system). The panel size is 1 Mpc.

4. Large-Scale Sloshing

5. Large-Scale Sloshing
Rossetti et al 2013
Rossetti M. et al.: Abell 2142 at large scales: An extreme case for sloshing?
Flux
Rossetti M. et al.: Abell 2142 at large scales: An extreme case for sloshing?
Temperature
Rossetti M. et al.: Abell 2142 at large scales: An extreme case for sloshing?
idual image from the azimuthal average in concentric annuli (left) and in elliptical annuli (right). X-ray contours are
dinates on the images are right ascension and declination.
his alternation of excesses and crossing of profiles
irections is a generic feature of the sloshing sce-
er et al. 2012) and was noticed also in Perseus by
paper (Roediger et al. in prep.).
In Fig. 8, we show a simulated residual image for A496 with
the orbit of the perturber in the plane of the sky that we rotated
Residuals
~1 Mpc
Abell 2142

6. Large-Scale Sloshing
Walker, Fabian, & Sanders 2014Figure 1. Top Left:Exposure corrected, background subtracted, point source subtracted and adaptively smoothed m
from XMM-Newton. Top Right: Chandra image of the same region in the 0.7-7.0keV band, showing two central
~800 kpc
RXJ2014.8-2430

7. • Information on this from simulations is currently limited due to:
• Most investigations of sloshing focused on the core region
• Algorithmic limitations (Roediger & ZuHone 2012)
• Small parameter space of simulations
~500 kpc
M ~ 1015 M⊙, R = 1:5,
b = 0.5 Mpc,
gasless subcluster,
~8 Gyr since core passage
M ~ 6 ×1014 M⊙, R = 1:3,
b = 1.5 Mpc,
gas-filled subcluster,
~8.5 Gyr since core passage
~1.5 Mpc

8. Sloshing and ICM Physics
Beyond Hydrodynamics

9. 200 kpc
A 2 1 4 2 A2142 wavelets
200 kpc

10. Roediger et al 2012
Irregular cold fronts in NG
Fig. 2.— Chandra/ACIS-S image of NGC 7618 in the
0.5-2.0 keV band, background-subtracted, exposure corrected,
Gaussian-smoothed to 6 arcsec. The logarithmic color scale is cho-
sen to highlight the substructure of the cold front. Prominent
features are labelled. The dashed arc marks the cold front.
Fig. 2.— Chandra/ACIS-S image of NGC 7618 in the
0.5-2.0 keV band, background-subtracted, exposure corrected,
Gaussian-smoothed to 6 arcsec. The logarithmic color scale is cho-
sen to highlight the substructure of the cold front. Prominent
features are labelled. The dashed arc marks the cold front.
Fig. 3.— Same as Fig. 2 but for UGC 12491, Gaussian-smoothed
to 4 arcsec.

11. • Large velocity shears exist across the cold front; the
fronts should be susceptible to the effects of the
Kelvin-Helmholtz instability
• Thermal conduction, if present, should smooth out
the temperature gradient
• What could stabilize the front surfaces against these
effects?
• Viscosity?
• Magnetic fields?
Cold Front Preservation

12. Magnetic Field Draping
Dursi & Pfrommer 2007 Asai et al 2007 ZuHone et al 2011
(see also: Vikhlinin et al 2001, Lyutikov 2006,
Keshet et al 2010, Reiss & Keshet 2012)

13. Sloshing with Magnetic Fields
T (keV) B (G)

14. Sloshing with Magnetic Fields
T (keV)
No Fields With Fields

15. Sloshing with Magnetic Fields
Metallicity (Z⊙)
No Fields With Fields

16. Entropy and Metallicity

17. ICM Microphysics
In the ICM, λmfp ≫ ρL, so momentum and heat
transport are modified strongly by the magnetic
field:
Π = −3ν∥
ˆbˆb −
1
3
I ˆbˆb −
1
3
I : ∇v
Q = −κ∥
ˆbˆb · ∇T

18. Viscosity and Cold Fronts
Viscous sloshing CF
Fig. 6.— Simulated X-ray images of the northern sloshing CF in the V
are for low and high viscosity (10 3 and 0.1 of the Spitzer value), resp
the right-hand-side column we added a random Poisson deviate to matc
Chandra/ACIS-I observation. The structure of the CF di↵ers between low
case (see labels), in both the ideal and in the noisy image.
Roediger et al 2013
Roedigeretal.2012
=0,103
,0.01and0.1
tyfµ103
,allCFs
ggedbytheKHI.With
comelessragged,and
scalesaresuppressed.
sicalviscosityof103
tperturbationspresent
y,thefrontsarealmost
scositycase(fµ=0.1)
atedby⇠40kpcalong
ongest(⇠500kms1
).
esthoughareabsentat
well,whereassmaller
ationatlowerviscosity.
attheviscosityismore
hanexpectedfromthe
alreasonsforthisdif-
edfromthelinearsta-
viscosityistoreduce
theflowparalleltothe
erturbationintheper-
thelinearanalysispre-
KHI,butstillagrowth,
uldshuto↵thegrowth
entthanexpected.We
icallyandnumerically
geretal.,inprepara-
CFsarecurvedinter-
gravitationalpotential
reastheanalyticesti-
nostratificationandno
rnCFsuppressesKHIs
ndwillthusslowdown
mewhatsmallerwave-
inthesimulations.Fi-
contactdiscontinuities
ythesloshingprocess,
maymodifyitsgrowth
heoutwardsmotionof
elengths,whichreduces
Churazov&Inogamov
EATURES
ages
imagesbyprojecting
ght(LOS),where⇤(T)
oSutherland&Dopita
yof0.3solar.Figure3
esfortheviscositysup-
µ=0.1.Wewillrefer
highviscosity,respec-
inviscid10 3 Spitzer viscosity
(”low viscosity case” in text)
10 2 Spitzer viscosity0.1 Spitzer viscosity
(”high viscosity case” in text)
Fig.2.—Temperatureslicesintheorbitalplaneatthefinal
timestep,forSpitzer-type,i.e.temperaturedependent,viscosities
withsuppressionfactorsfµ=0,103,0.01and0.1fromtopto
bottom.Increasingtheviscosityerasesprogressivelylargersub-
structurealongthefronts.Wehaveorientedtheimagessuchthat
theycomparetothesituationobservedinVirgo,i.e.northisup
4Roedigeretal.2012
planeatthefinaltimestepforfµ=0,103
,0.01and0.1
fromtoptobottom.Ataviscosityfµ103
,allCFs
areclearlydistortedandmaderaggedbytheKHI.With
increasingviscosity,thefrontsbecomelessragged,and
structuresatprogressivelylargerscalesaresuppressed.
Interestingly,eventhesmallphysicalviscosityof103
Spitzererasessomeofthesmallestperturbationspresent
intheinviscidsimulation.Finally,thefrontsarealmost
completelysmoothinthehighviscositycase(fµ=0.1)
exceptfortwolargeKHrollsseparatedby⇠40kpcalong
theSW,wheretheshearflowisstrongest(⇠500kms1
).
Distortionsatsmallerlengthscalesthoughareabsentat
highviscosityatthislocationaswell,whereassmaller
distortionsarepresentatthislocationatlowerviscosity.
Oursimulationsdemonstratethattheviscosityismore
ecientinsuppressingtheKHIthanexpectedfromthe
linearanalysis.Thereareseveralreasonsforthisdif-
ference:thegrowthtimeisderivedfromthelinearsta-
bilityanalysis.Thee↵ectoftheviscosityistoreduce
shearvelocities,whichappliestotheflowparalleltothe
interfaceaswellasthevelocityperturbationintheper-
pendiculardirection.Thus,whilethelinearanalysispre-
dictsonlyaslowedgrowthoftheKHI,butstillagrowth,
atlongertimescalesviscosityshouldshuto↵thegrowth
completelyandthusbemoreecientthanexpected.We
demonstratethisbehavioranalyticallyandnumerically
inaseparatepublication(Roedigeretal.,inprepara-
tion).Furthermore,thesloshingCFsarecurvedinter-
facesembeddedinabackgroundgravitationalpotential
inviscid10 3 Spitzer viscosity
(”low viscosity case” in text)
r viscosity

19. Viscosity and Cold Fronts
ZuHone et al 2014a, arXiv:1406.4031

20. Viscosity and Cold Fronts
ZuHone et al 2014a, arXiv:1406.4031

21. Viscosity and Cold Fronts
ZuHone et al 2014a, arXiv:1406.4031
similar

22. Viscosity and Cold Fronts
ZuHone et al 2014a, arXiv:1406.4031
dissimilar

23. – 27 –
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
0 10 20 30 40 50 60
T(keV)
d (kpc)
a
S1
SC1
SC3
SC4
3.5
4
4.5
5
5.5
6
6.5
0 5 10 15 20 25 30 35 40 45 50
T(keV)
d (kpc)
b
S1
SC1
SC3
SC4
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
0 5 10 15 20 25 30 35 40 45 50
T(keV)
d (kpc)
c
S1
SC1
SC3
SC4
3.5
4
4.5
5
5.5
6
6.5
7
7.5
0 10 20 30 40 50
T(keV)
d (kpc)
d
S1
SC1
SC3
SC4
No Conduction
Spitzer
0.1 Spitzer
Sloshing and Thermal Conduction
(ZuHone et al 2013a)

24. A2319
S1
SC1
SC3No Conduction 0.1 Spitzer
Spitzer
Sloshing and Thermal Conduction
(ZuHone et al 2013a)

25. Sloshing and
Radio Mini-Halos

26. Radio Mini-Halos
• Steep spectra
• Steep radial cutoff
• Not all cool-core
clusters possess them
Giacintucci et al 2014

27. Models
• CRe which produce ~GHz emission have tcool ≪ tdiff, so we
need a replenishing source
• Reacceleration models:
• Turbulence reaccelerates existing population of CRe with γ
~ few hundred up to γ ~ 10
4
• Hadronic/secondary models:
• pCR + pth π
0
+ π
+
+ π
-
+ anything
π
±
μ
±
+ νμ
μ
±
e
±
+ νμ + νe
π
0
2γ

28. No emission from
these electrons
Emission from these
electrons
ZuHone et al 2013b
Projected Mass-Weighted vturb (km/s)
Reacceleration Models

29. Radio-Emitting
Particles
(327 MHz)
ZuHone et al 2013b
Reacceleration Models

30. NW
SE
0 50 100 150 200 250
r (kpc)
10−8
10−7
10−6
10−5
10−4
10−3
10−2
10−1
1
Sν(η/10−3
)(mJyarcsec−2
)
NW Radio
SE Radio
NW Temperature
SE Temperature
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
T(keV)
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
T(keV)
ZuHone et al 2013b
Reacceleration Models

31. Spectral SteepeningMapping particle acceleration in RX J1720.1+2638
0.5
1.5
2.5
spectral index
beam
C
50 kpc
6
5
4
3
2
1
a b
— (a) Grayscale image of the spectral index distribution between 617 MHz and 1480 MHz in the minihalo and head-tail radio galaxy. The im
puted from images with similar noise (30 µJy beam−1) and same u−v range and restoring beam of 8′′ × 6′′. Overlaid are the 617 MHz conto
Giacintucci et al 2014

32. ZuHone et al 2014b, arXiv:1403.6743
Hadronic Models
Spectral steepening from rapid changes in B (Keshet 2010)

33. ZuHone et al 2014b, arXiv:1403.6743
Hadronic Models

34. Summary
• Lots of activity, in both observations and simulations
• Some big open questions:
• How do you form large-scale fronts? With bigger kicks?
Something particular about the thermodynamic profiles?
• Does the presence of sharp fronts really constrain thermal
conduction to be very small?
• What is the ICM viscosity? How do we distinguish the effect
of viscosity from that of the magnetic field by itself? Can we?
• What is the origin of radio mini-halos? How do we explain
spectral steepening like in RXJ1720?