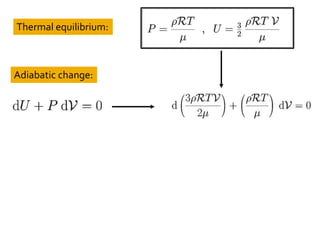
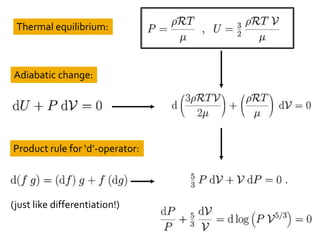
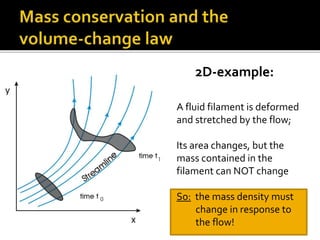
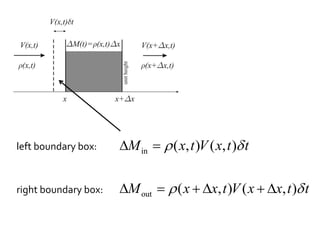
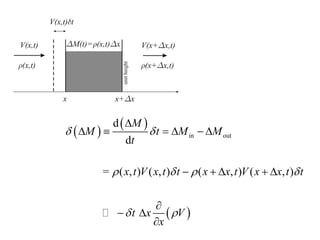
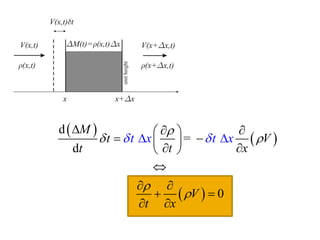
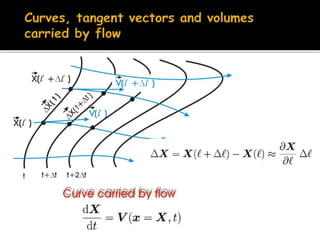
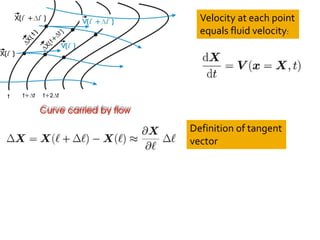
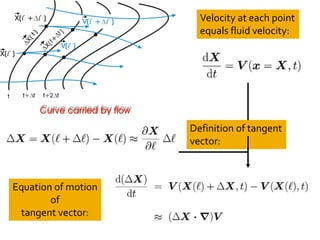
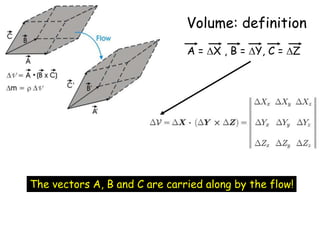
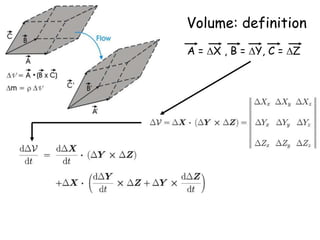
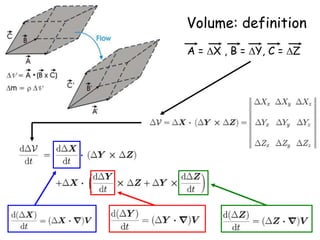
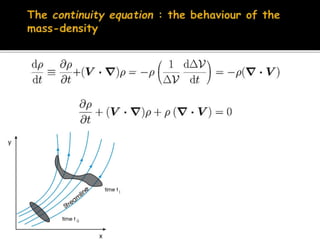
1) The document discusses the equations of motion and properties of gases, including the relationship between pressure and thermal velocity, and how pressure forces relate to changes in internal energy and volume. 2) It also covers how mass density must change in response to fluid flow in order to satisfy mass conservation, and derives the equation governing volume change using an orthogonal triad of vectors carried along by the flow. 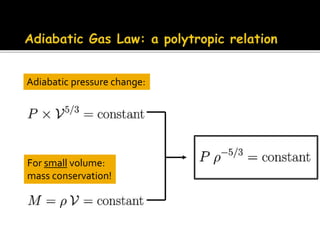3) The general volume-change law is presented, along with the requirement of mass conservation expressed as the density times the volume change remaining constant.

1. Prof. dr. A. Achterberg, Astronomical Dept. , IMAPP, Radboud Universiteit

2. -Equation of motion;
-Relation between pressure
and thermal velocity dispersion;
-Form of the pressure force

3. Each degree of freedom carries an energy 1
b
2 k T
2 2 2
1 1 1 1
b
2 2 2 2
2 2
b b
b
3 3
x y z
m m m k T
k T k T
P nk T
m m
  
 
 
  

 
    
 
 
Point particles with mass m:

4. b
H
H
universal gas constant;
= mass in units of mass hydrogen atom.
T
P
k
m
m
m




 

R
R

5. Adiabatic change: no energy is irreversibly
lost from the system, or gained by the system
d d = 0
U P
 V

6. Adiabatic change: no energy is irreversibly
lost from the system, or gained by the system
d d = 0
U P
 V
Change in internal
energy U
Work done by pressure forces
in volume change dV

7.  
2 3 3
1
th b
2 2 2
kinetic energy of
thermal motion
2
th
3
T
n m nk T
T
P





  
 
R
W
R
W
Thermal
energy density:
Pressure:

8. Thermal equilibrium:
Adiabatic change:

9. Thermal equilibrium:
Adiabatic change:
Product rule for ‘d’-operator:
(just like differentiation!)

10. Adiabatic pressure change:
For small volume:
mass conservation!

11. 1
th
'
1 ( 1)
5
, =1:
3
P K
T K
T
P
P T
W







  
 






 






 
 

R
R
Polytropic gas law:
Ideal gas law:
Thermal energy density:
Polytropic index
mono-atomic gas: ISOTHERMAL

12. A fluid filament is deformed
and stretched by the flow;
Its area changes, but the
mass contained in the
filament can NOT change
So: the mass density must
change in response to
the flow!
2D-example:

14. in
out
( , ) ( , )
( , ) ( , )
M x t V x t t
M x x t V x x t t
 
 
 
     
left boundary box:
right boundary box:

15.  
 
 
in out
d
d
= ( , ) ( , ) ( , ) ( , )
M
M t M M
t
x t V x t t x x t V x x t t
t x V
x
 
   
 

     
    

 


16.  
 
 
d
=
d
0
M
t V
t t x
t x t x
V
t x

 


 
  
 
 
 
 
 

 







17.      
 
0
0
x y z
V V V
t x y z
t

  


   
   
   

  

Ñ V

19. Velocity at each point
equals fluid velocity:
Definition of tangent
vector

20. Velocity at each point
equals fluid velocity:
Definition of tangent
vector:
Equation of motion
of
tangent vector:

21. Volume: definition
A = X , B = Y, C = Z
The vectors A, B and C are carried along by the flow!

22. Volume: definition
A = X , B = Y, C = Z

23. Volume: definition
A = X , B = Y, C = Z

24. Special choice:
orthogonal triad
General
volume-change
law

25. Special choice:
Orthonormal triad
General
Volume-change
law

26. Volume
change
Mass conservation:  V = constant

27. Volume
change
Mass conservation:  V = constant
Comoving
derivative

29. Divergence product rule

31. &