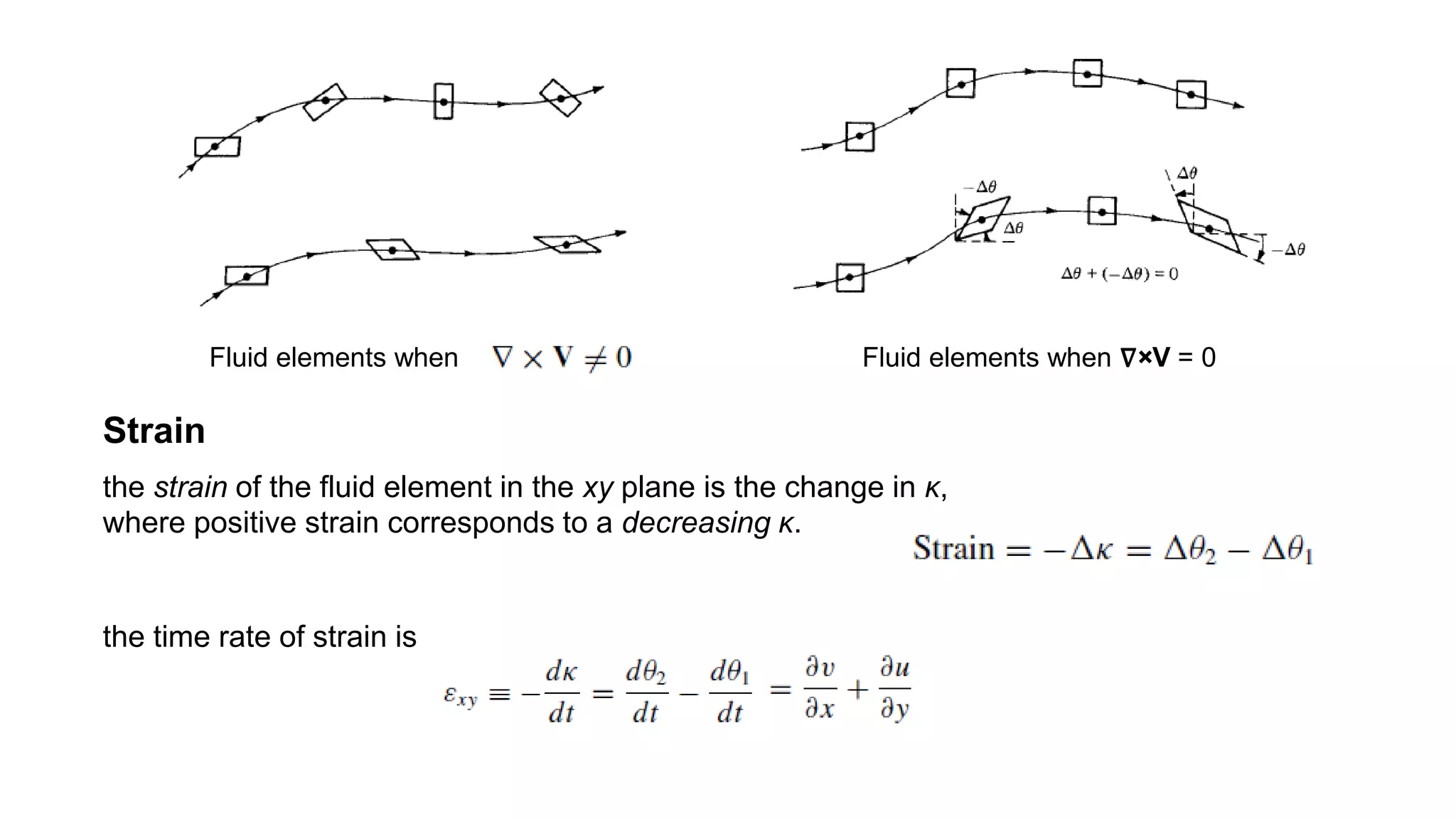
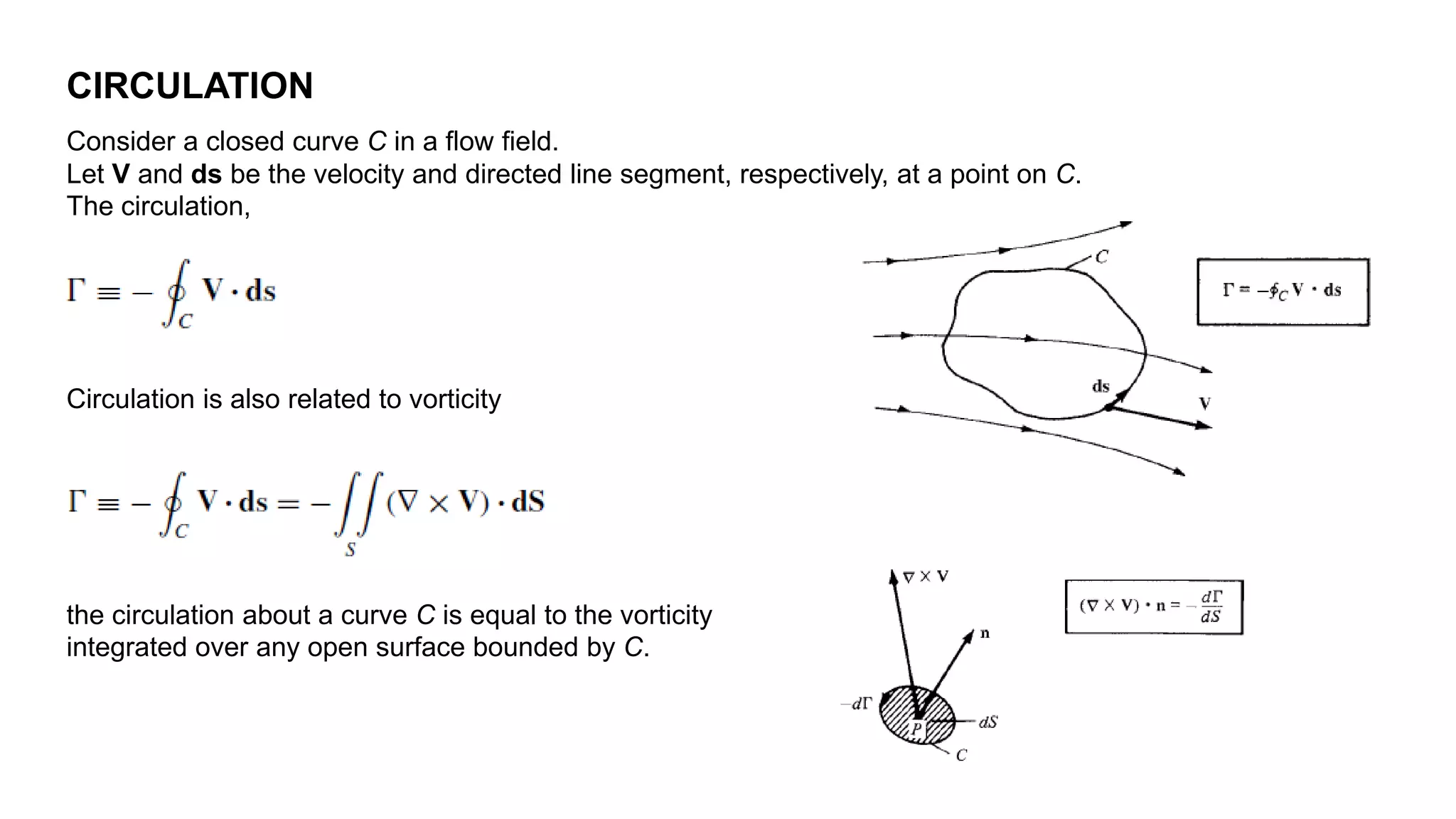
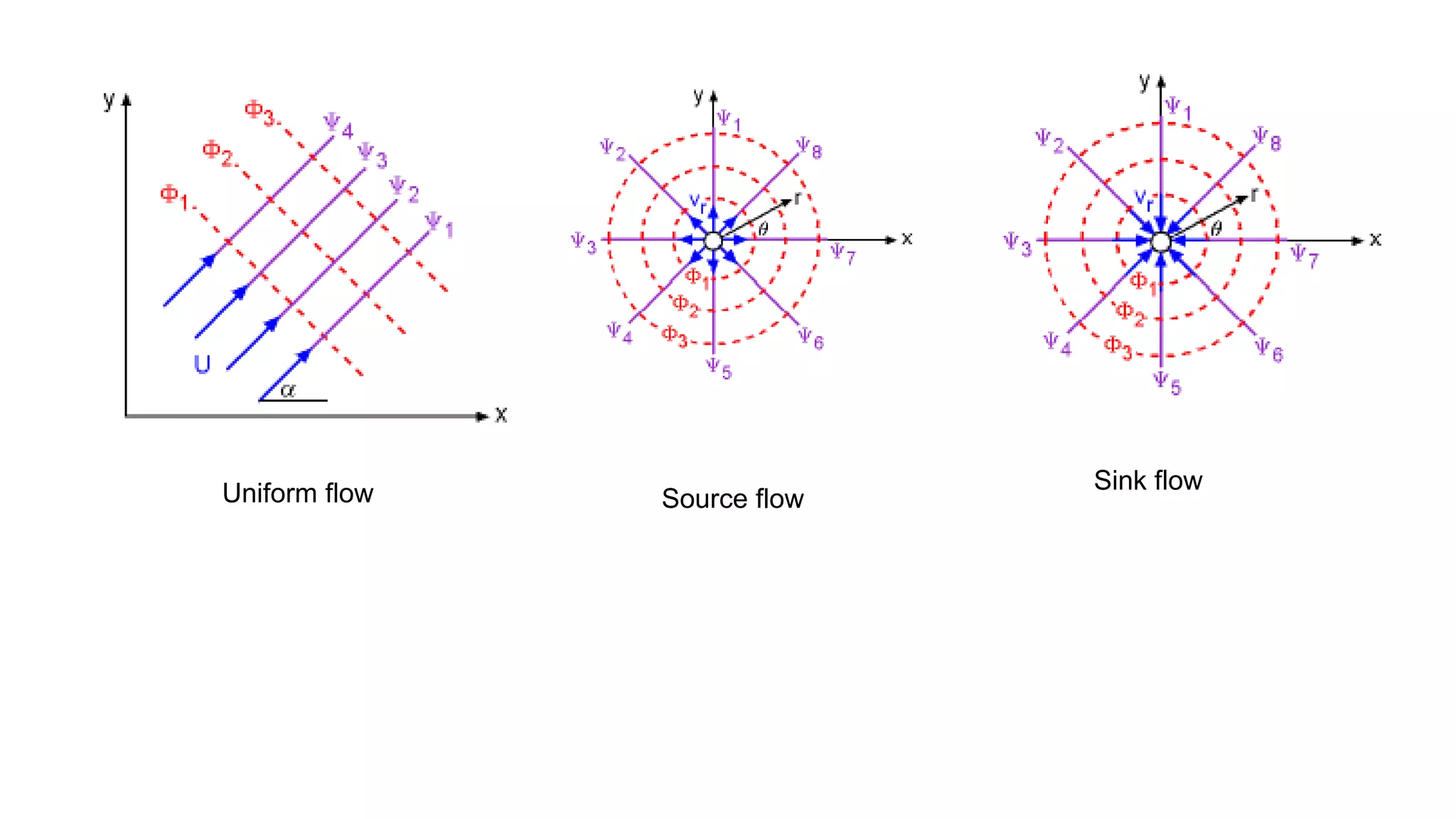
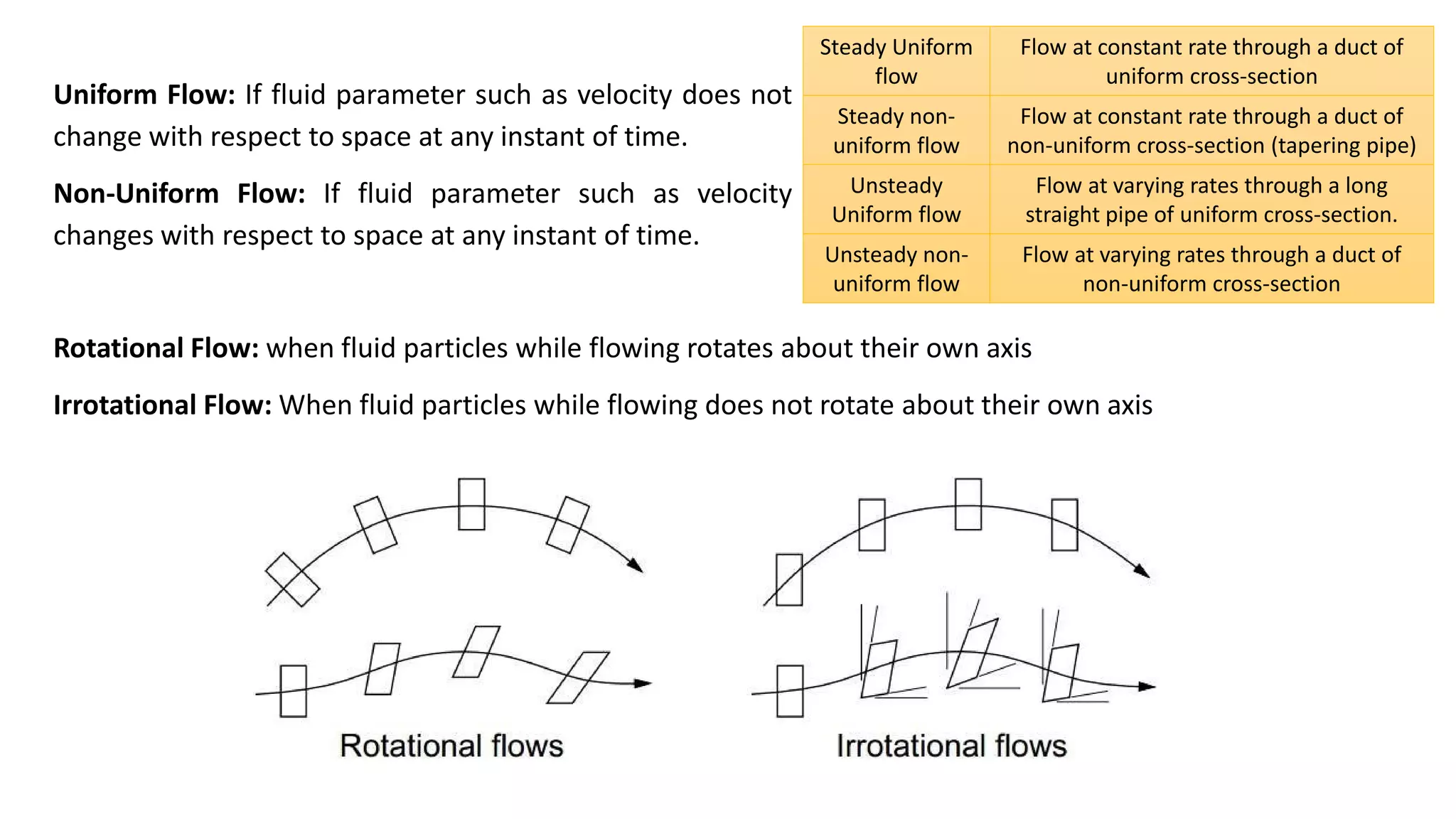
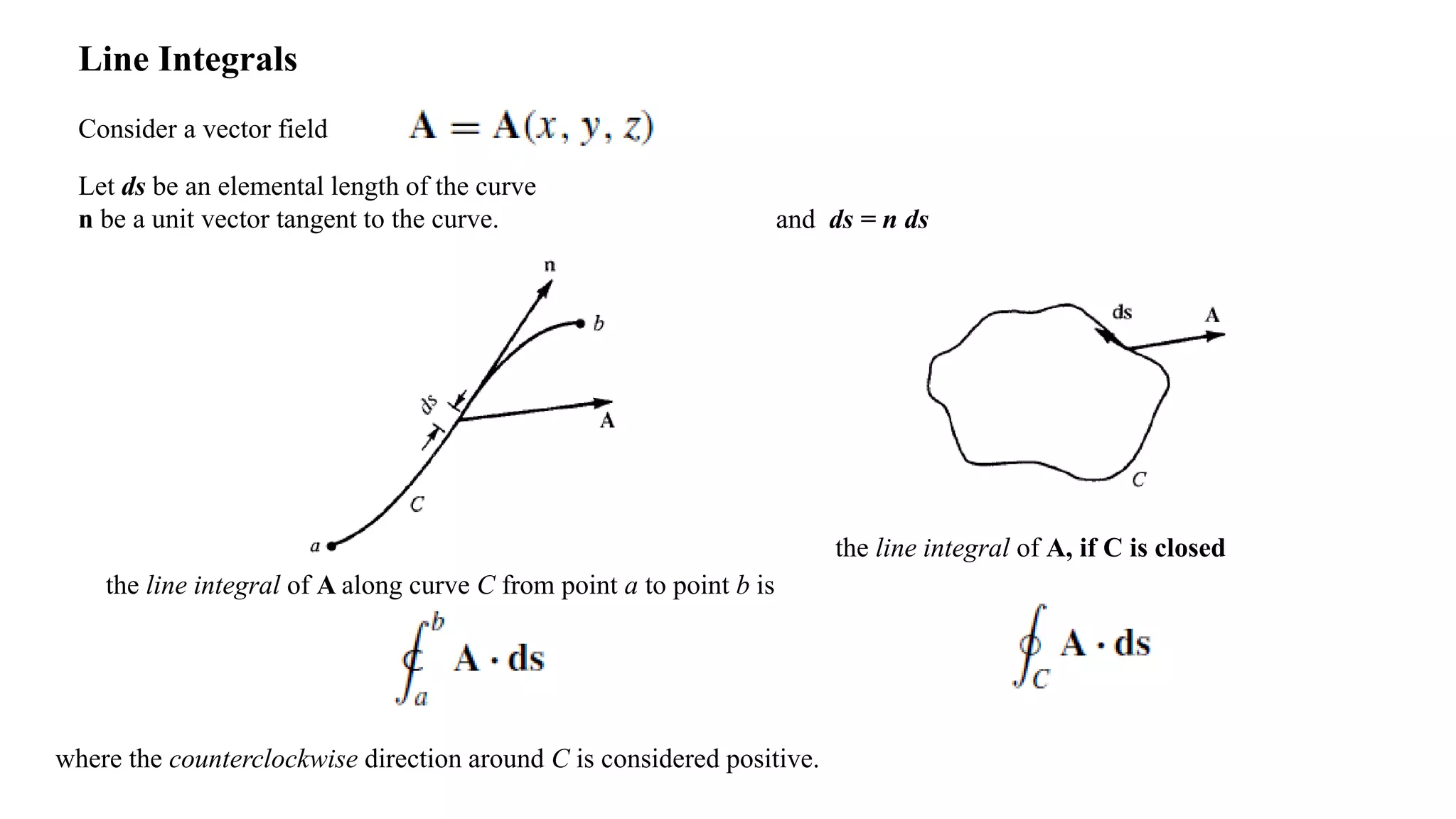
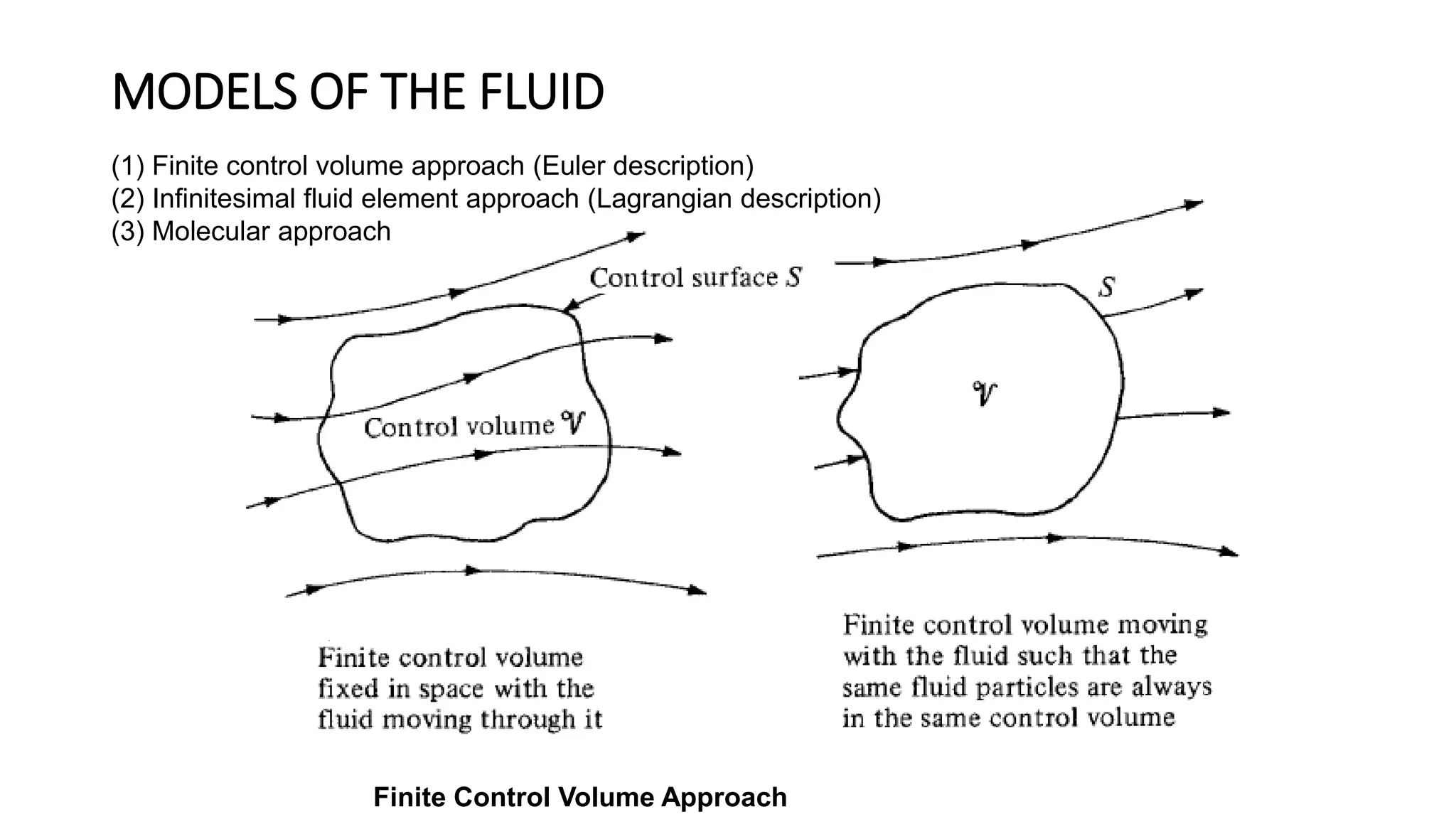
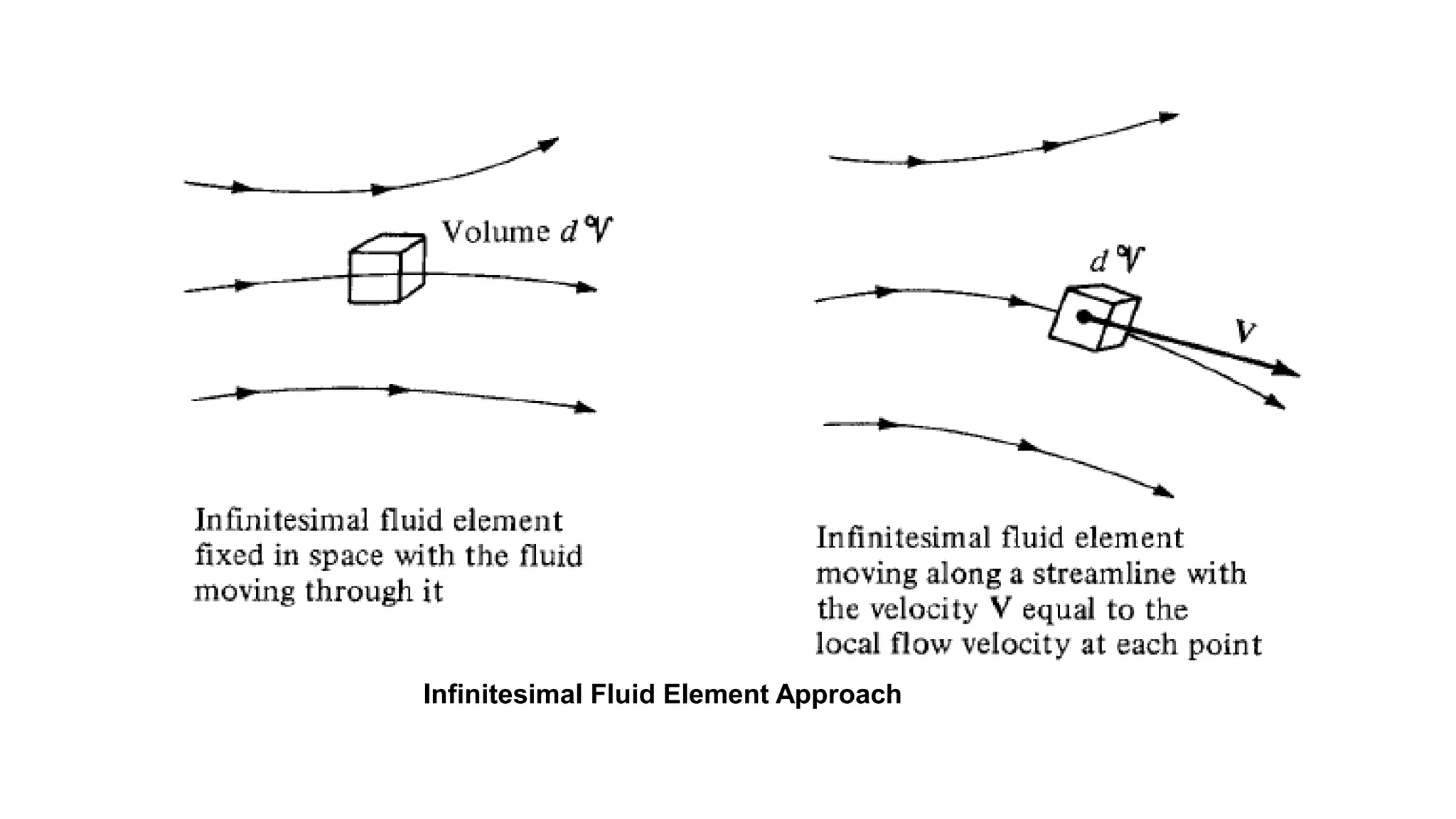
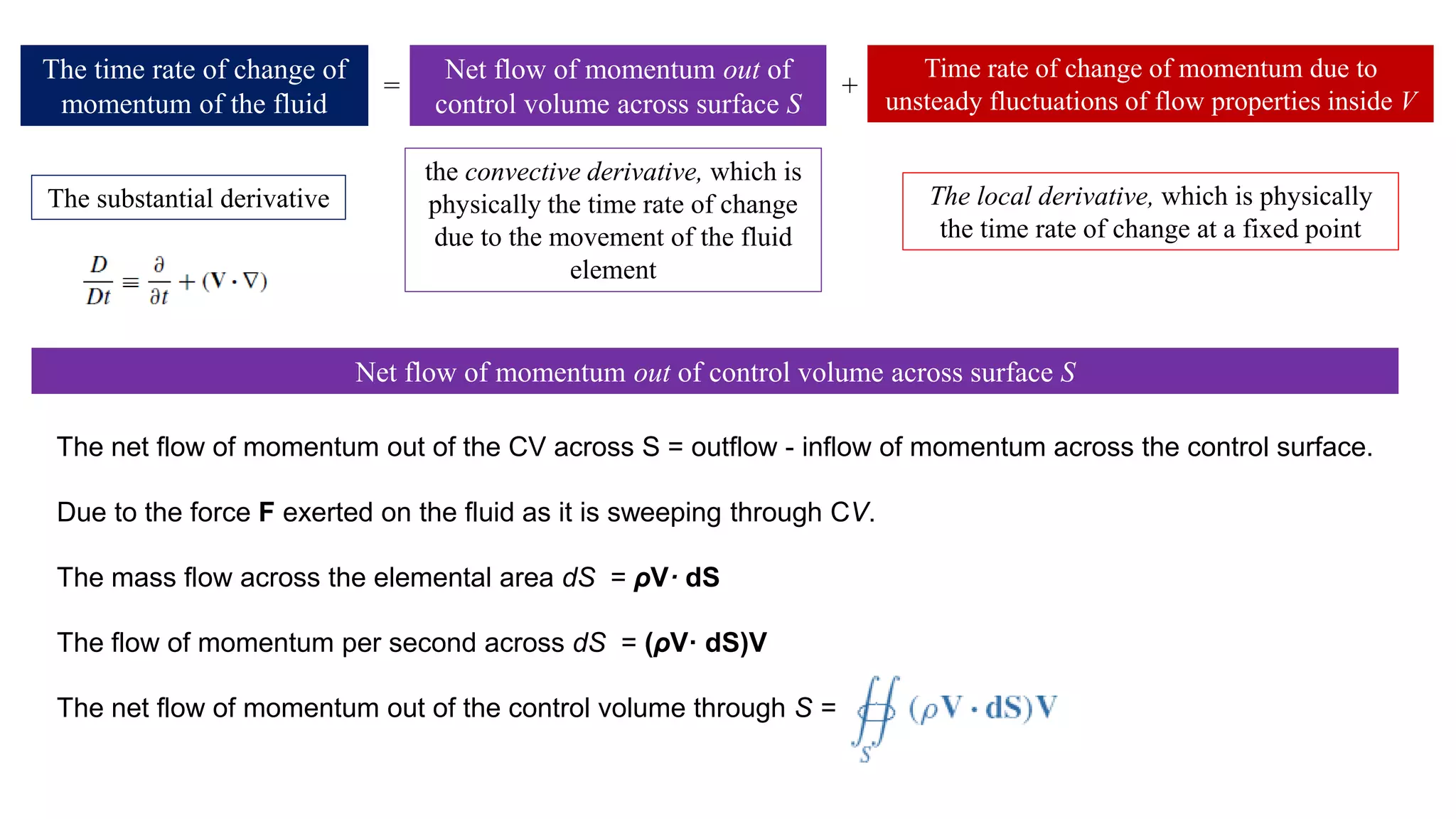
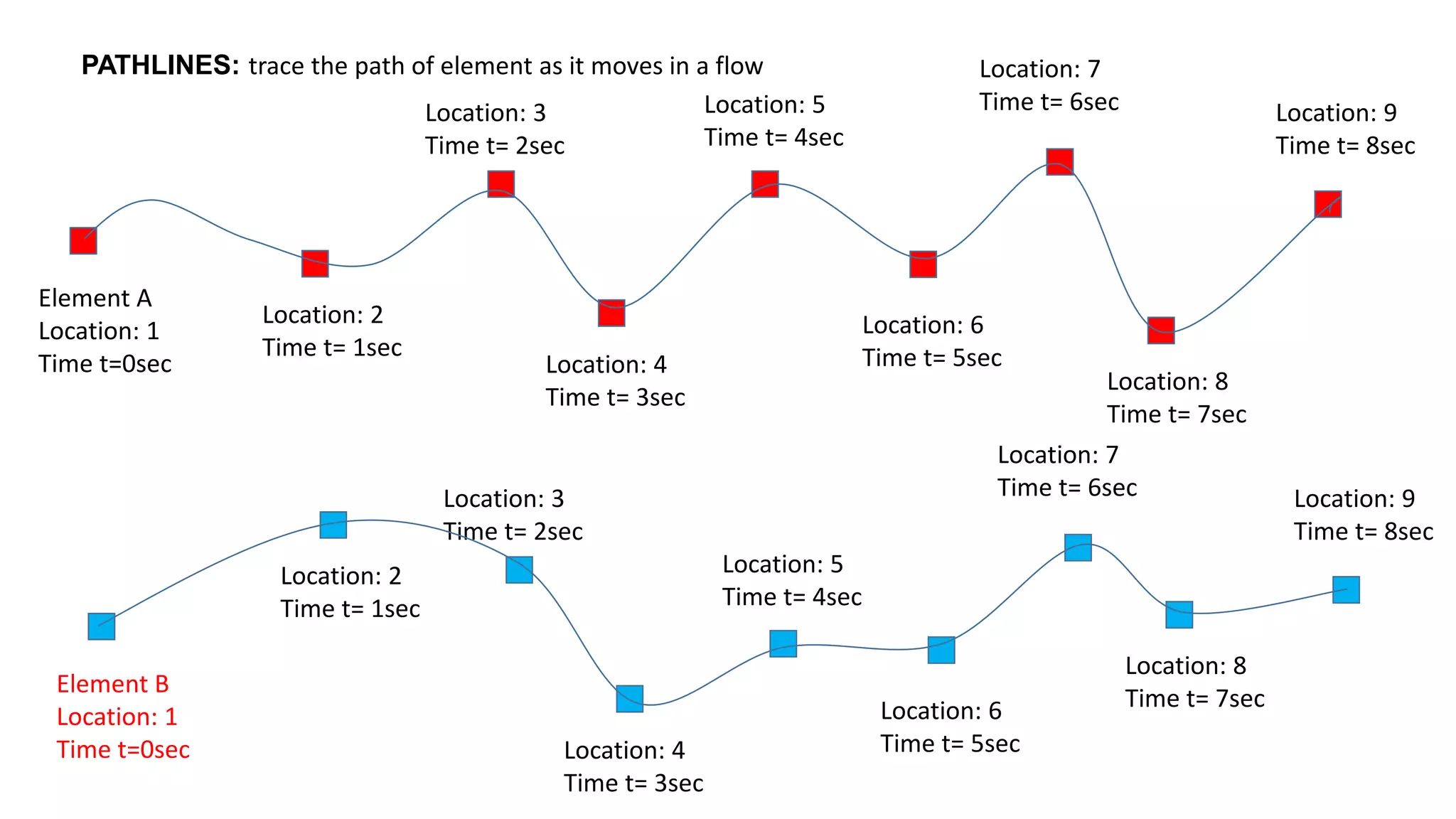
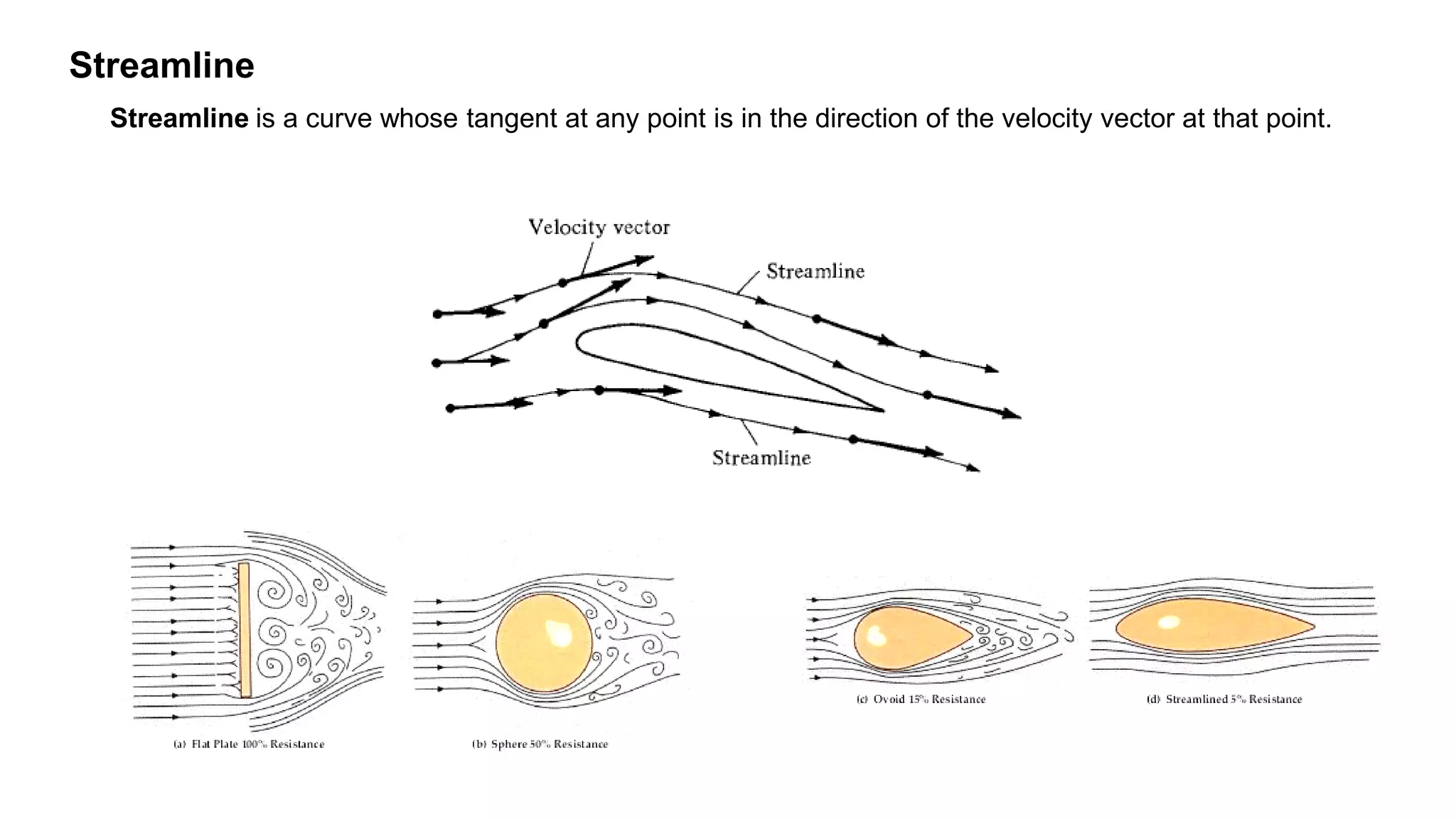
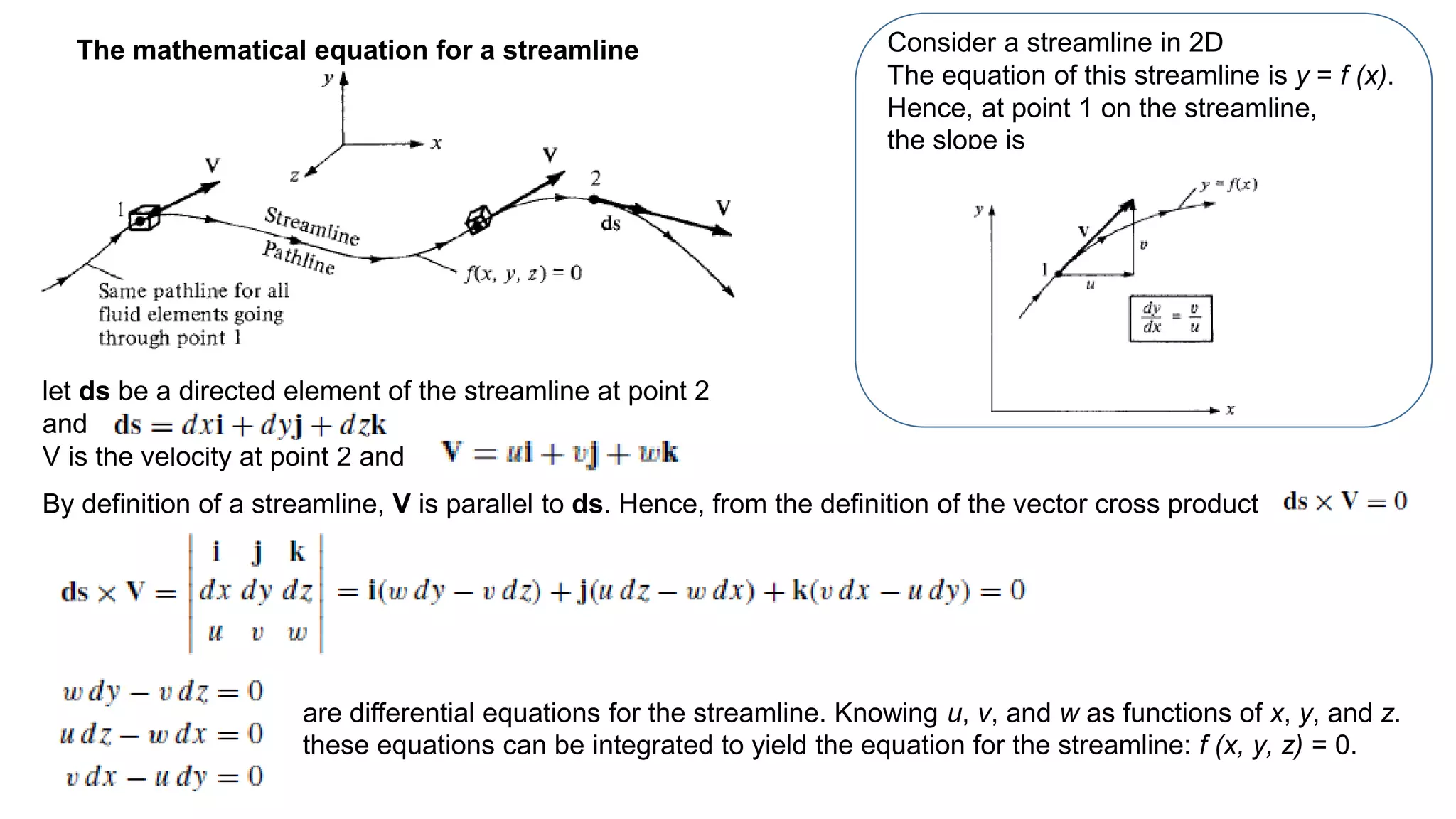
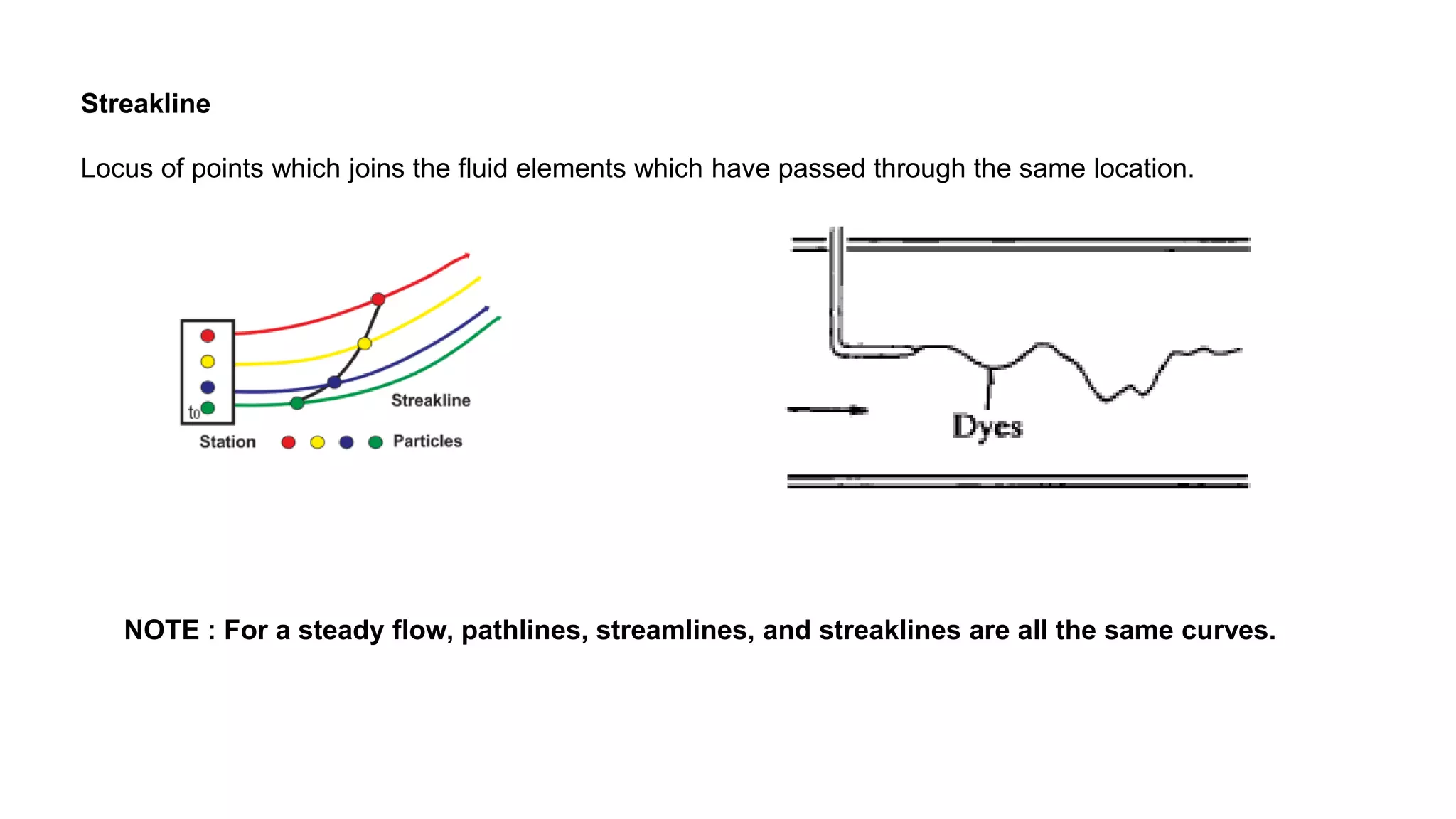
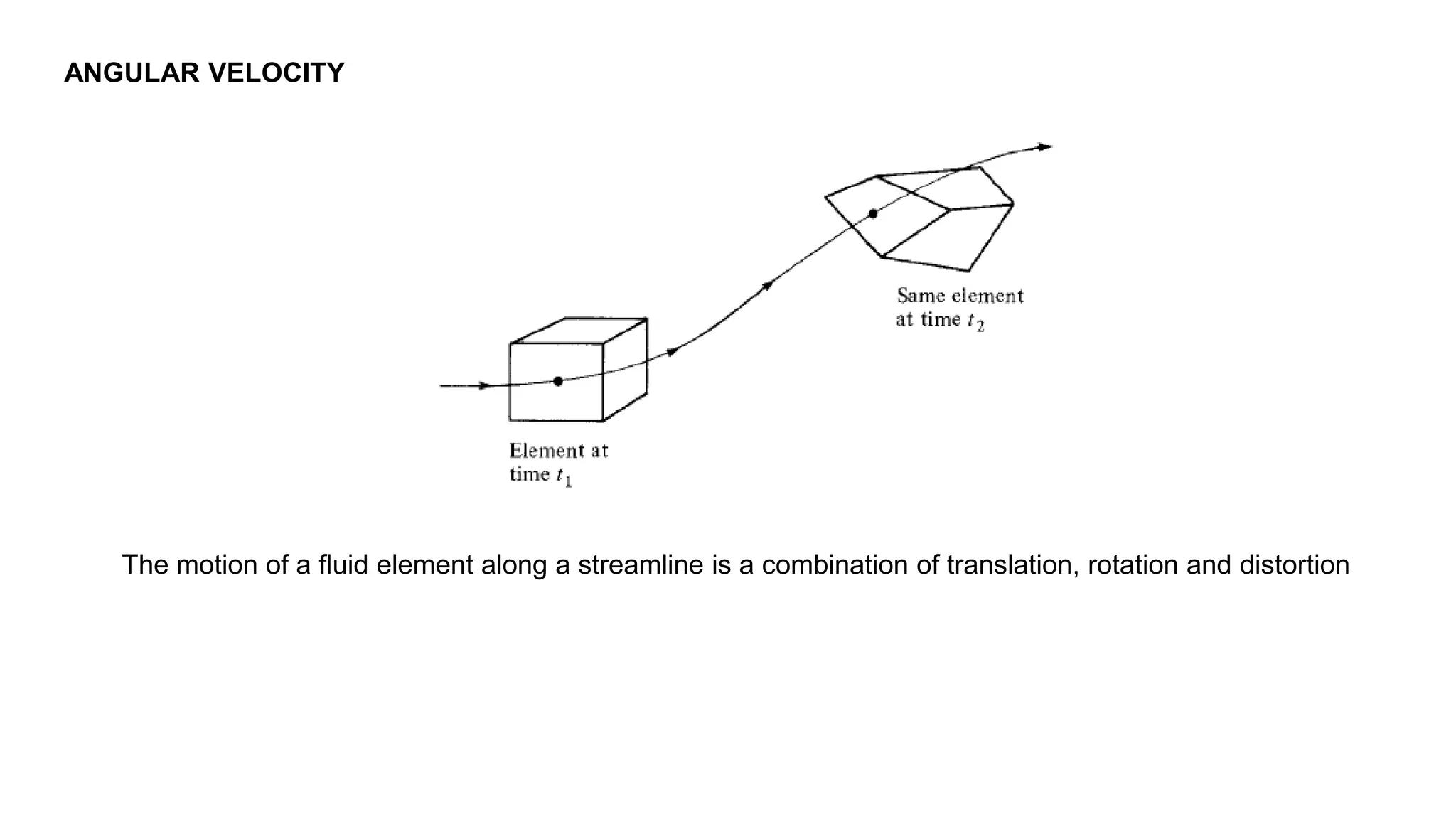
The document provides information about various concepts in aerodynamics including: 1) It defines types of fluid flow such as steady/unsteady, incompressible/compressible, uniform/non-uniform, rotational/irrotational, viscous/inviscid, laminar/turbulent flows based on factors like density, velocity gradients. 2) It describes concepts like continuity, momentum and energy equations, control volume approach, pathlines, streamlines, streaklines, angular velocity, vorticity, and circulation. 3) It discusses Mach number regimes including subsonic, transonic, sonic, supersonic and hypersonic flows and how compressibility effects vary with Mach number

1. Aerodynamics
Air + Dynamics

2. Aerodynamics – I
Sub Code : 18AE42
UNIT I
Review of Basic Fluid Mechanics: Continuity, momentum and energy equation,
units and dimensions, Types of flow, compressibility, Mach number regimes.
Description of Fluid Motion: Euler and Lagrangian descriptions, Control volume
approach to continuity and momentum equations, Pathlines, Streamlines and
Streaklines, Angular velocity, Vorticity, Circulation, Stream function, Velocity
potential and Relationship between them.
Faculty Name: Siddalingappa PK, Asst Prof, Dept of Aeronautical Engineering, NMIT Bengaluru

3. Dimensions and Units
A dimension is a measure of a physical quantity, while a unit is a way to assign a number to
that dimension. For example, length is a dimension that is measured in units such as
microns, feet (ft), centimeters (cm), meters (m), kilometers (km), etc.
For example, force has the same dimensions as
mass times the acceleration (by Newton’s second
law). Thus, in terms of primary dimensions,
Primary dimensions and their associated
primary SI unit are as follows

4. Some Quantity,
Dimensions and their
associated primary SI unit
are as follows

5. Properties of fluids: Properties of fluids determine how fluids can be used
in engineering and technology.
The following are some of the important basic properties of fluids:
• Density
• Viscosity
• Temperature
• Pressure
• Specific Volume
• Specific Weight
• Specific Gravity

6. Types of Flow
According to nature of flows and their dependency on other factors such as density, velocity gradient, etc. flows are
divided into various types.
• Steady Flow & Unsteady Flow
• Incompressible Flow & Compressible Flow
• Uniform Flow & Non-Uniform Flow
• Rotational Flow & Irrotational Flow
• Viscous Flow & Inviscid Flow
• Laminar Flow & Turbulent Flow
• Based on Mach number
1. Subsonic flow
2. Transonic flow
3. Sonic flow
4. Supersonic flow
5. Hypersonic flow

7. • Steady Flow: If fluid parameters such as velocity, acceleration, etc
does not change with respect to time.
• Unsteady Flow: If fluid parameters such as velocity, acceleration, etc
changes with respect to time.
• Incompressible Flow: type of flow in which density of fluid remains
constant. It means fluid is incompressible.
• Compressible Flow: is flow in which density of fluid changes with
respect to time and distance.

8. Uniform Flow: If fluid parameter such as velocity does not
change with respect to space at any instant of time.
Non-Uniform Flow: If fluid parameter such as velocity
changes with respect to space at any instant of time.
Steady Uniform
flow
Flow at constant rate through a duct of
uniform cross-section
Steady non-
uniform flow
Flow at constant rate through a duct of
non-uniform cross-section (tapering pipe)
Unsteady
Uniform flow
Flow at varying rates through a long
straight pipe of uniform cross-section.
Unsteady non-
uniform flow
Flow at varying rates through a duct of
non-uniform cross-section
Rotational Flow: when fluid particles while flowing rotates about their own axis
Irrotational Flow: When fluid particles while flowing does not rotate about their own axis

9. Viscous Flow: When viscosity of fluid is considered in
fluid flow, such type of flow is known as viscous flow.
Inviscid Flow: When viscosity of fluid is not considered
in fluid flow, such type of flow is known as Inviscid flow.
Laminar Flow: The flow in which fluid flows smoothly
such that fluid layers are parallel to each other or no to
streamlines intersect each other, such type of flow is
known as laminar flow.
Turbulent Flow: The flow in which fluid flows in zig-zag
manner and fluctuate irregularly in such a way that its
velocity changes irregularly, such type of flow is known
as turbulent flow.

10. Subsonic flow: Range 0 < M < 0.7
Transonic flow: Range 0.7 < M < 1.2
Sonic flow: Mach number is one (M = 1)
Supersonic flow: Range 1.2 < M < 3. Compressibility effects are
important for supersonic aircraft, and shock waves are generated by
the surface of the object.
Hypersonic flow: when M > 5. At these speeds, some of the energy
of the object now goes into exciting the chemical bonds which hold
together the nitrogen and oxygen molecules of the air.
Mach number: The ratio of the speed of the object/air to the speed of sound in the gas
determines the magnitude of many of the compressibility effects.

11. Gradient of a Scalar Field
Consider a scalar field
Divergence of a Vector Field
Consider a vector field
Curl of a Vector Field
Consider a vector field
∇ ·V is physically the time rate of
change of the volume of a
moving fluid element, per unit
volume

12. Line Integrals
Consider a vector field
Let ds be an elemental length of the curve
n be a unit vector tangent to the curve. and ds = n ds
the line integral of A along curve C from point a to point b is
the line integral of A, if C is closed
where the counterclockwise direction around C is considered positive.

13. Surface Integrals
Consider an open surface S bounded by the closed curve C
At point P on the surface, let dS be an elemental area of the surface
and dS = n dS.
n be a unit vector normal to the surface.
The orientation of n is in the direction according to the right-hand rule for movement along C
The surface integral over the surface S can be defined as
If the surface S is closed, n points out of the
surface.
The surface integrals over the closed surface are

14. Volume Integrals
Consider a volume V in space.
Let ρ be a scalar field in this space.
The volume integral over the volume V of the quantity ρ is
volume integral of a scalar ρ over the volume V
Let A be a vector field in space.
The volume integral over the volume V of the quantity A is
volume integral of a vector A over the volume V

15. Relations Between Line, Surface, and Volume Integrals
Let A be a vector field.
The line integral of A over C is related to the surface integral of A over S by Stokes’ theorem:
The surface and volume integrals of the vector field A are related through the divergence theorem:
If p represents a scalar field, a vector relationship is given by the gradient theorem:

16. MODELS OF THE FLUID
Finite Control Volume Approach
(1) Finite control volume approach (Euler description)
(2) Infinitesimal fluid element approach (Lagrangian description)
(3) Molecular approach

17. Infinitesimal Fluid Element Approach

18. CONTINUITY EQUATION
Physical principle: Mass can be neither created nor destroyed.
Consider the fixed finite control volume V.
At a point on the control surface S, the flow velocity is V
dS is the vector elemental surface area
dV is an elemental volume inside the control volume.
Apply the physical principle to the control volume.

19. Net mass flow out of control volume through surface S
Mass flow = density × area × component of flow velocity normal to the area
Mass flow across the Elemental surface area dS = ρ dS V
Here dS always points in a direction out of the control volume.
V also points out of the control volume, so that
the product ρV· dS is positive.
i.e mass flow is physically leaving the control volume (outflow).
The net mass flow out of the entire control surface S = Sum of ρV·dS over S

20. Time rate of decrease of mass inside control volume V
Mass = Density × Volume
Consider the elemental volume dV inside the Control volume V
Mass inside the elemental volume dV, is dm = ρdV
Total mass inside the control volume V, is sum of dm over V =
The time rate of increase of mass inside the control volume V =
The time rate of decrease of mass inside the control volume V =
is called the
continuity equation
in integral form.

21. Since the control is fixed in space, the limits of integration are also fixed.
Hence, the time derivative can be placed inside the volume integral
Now, Apply the divergence theorem,
is the continuity equation in the form of a partial differential equation and it relates the flow field variables
at a point in the flow, which deals with a finite space.

22. For the steady flow :
For an incompressible flow :
0
0 Constant

23. MOMENTUM EQUATION
Physical principle: Force = time rate of change of momentum
Consider the fixed finite control volume V.
At a point on the control surface S, the flow velocity is V
dS is the vector elemental surface area
dV is an elemental volume inside the control volume.
F = ma
where F is the force exerted on a body of mass m and a is the acceleration.
mV is the momentum of a body of mass m.
Newton’s second law,

24. Expression for F
F: the force exerted on the fluid as it flows through the control volume.
Sources of this force
Body forces Surface forces
Let f be the net body force per unit mass exerted on
the fluid inside CV.
The body force on the elemental volume dV = ρfdV
The total body force exerted on the fluid in the CV =
The elemental surface force due to pressure acting on the
element of area dS = −pdS
The total pressure over the entire control surface =
Fviscous is the total viscous force exerted on the control surface.
The total force experienced by the fluid as it is sweeping through the fixed control volume is
gravity, electromagnetic forces, etc pressure and shear stress acting on the control surface S

25. The time rate of change of
momentum of the fluid
Net flow of momentum out of
control volume across surface S
Time rate of change of momentum due to
unsteady fluctuations of flow properties inside V
= +
The local derivative, which is physically
the time rate of change at a fixed point
the convective derivative, which is
physically the time rate of change
due to the movement of the fluid
element
The substantial derivative
Net flow of momentum out of control volume across surface S
The net flow of momentum out of the CV across S = outflow - inflow of momentum across the control surface.
Due to the force F exerted on the fluid as it is sweeping through CV.
The mass flow across the elemental area dS = ρV· dS
The flow of momentum per second across dS = (ρV· dS)V
The net flow of momentum out of the control volume through S =

26. Time rate of change of momentum due to unsteady fluctuations of flow properties inside CV
The momentum of the fluid in the elemental volume dV = (ρ dV)V
The momentum contained at any instant inside the control volume =
Time rate of change of momentum due to unsteady flow fluctuations =
is the momentum equation in integral form.
and
Newton’s second law,

27. The momentum equation in integral form.
Apply the gradient theorem
The x component of the above equation using V = ui + vj + wk in Cartesian coordinates can be
Apply the divergence theorem

28. The x component of momentum equation is
x component of momentum equation
y component of momentum equation
z component of momentum equation
The above expression are the momentum equations, in partial differential form which relate flow-field
properties at any point in the flow.

29. The momentum equation for the steady, 3D, inviscid flow with no body forces, can be written as
The above momentum equations for an inviscid flow are called the Euler equations.
The momentum equations for a viscous flow are called the Navier-Stokes equations.

30. PATHLINES: trace the path of element as it moves in a flow
Element A
Location: 1
Time t=0sec
Location: 3
Time t= 2sec
Location: 2
Time t= 1sec
Location: 4
Time t= 3sec
Location: 5
Time t= 4sec
Location: 6
Time t= 5sec
Location: 7
Time t= 6sec
Location: 8
Time t= 7sec
Location: 9
Time t= 8sec
Element B
Location: 1
Time t=0sec
Location: 3
Time t= 2sec
Location: 2
Time t= 1sec
Location: 4
Time t= 3sec
Location: 5
Time t= 4sec
Location: 6
Time t= 5sec
Location: 7
Time t= 6sec
Location: 8
Time t= 7sec
Location: 9
Time t= 8sec

31. Streamline
Streamline is a curve whose tangent at any point is in the direction of the velocity vector at that point.

32. let ds be a directed element of the streamline at point 2
and
V is the velocity at point 2 and
The mathematical equation for a streamline
are differential equations for the streamline. Knowing u, v, and w as functions of x, y, and z.
these equations can be integrated to yield the equation for the streamline: f (x, y, z) = 0.
By definition of a streamline, V is parallel to ds. Hence, from the definition of the vector cross product
Consider a streamline in 2D
The equation of this streamline is y = f (x).
Hence, at point 1 on the streamline,
the slope is

33. Streakline
Locus of points which joins the fluid elements which have passed through the same location.
NOTE : For a steady flow, pathlines, streamlines, and streaklines are all the same curves.

34. ANGULAR VELOCITY
The motion of a fluid element along a streamline is a combination of translation, rotation and distortion

35. Consider an infinitesimal fluid element in 2D flow
in XY plane.
At time t the shape of this fluid element is
rectangular
After some time t + Δt, Assume that the fluid element
is moving upward and to the right
During the time increment Δt, the sides AB and AC
have rotated through the angular displacements −Δθ1
and Δθ2, respectively.
Consider the velocity in the y direction.
At point A at time t, this velocity is v,
Point C is a distance dx from point A; hence, at
time t the vertical component of velocity of point
C is given by v+(∂v/∂x) dx
Distance in y direction that A moves during time increment Δt =
Distance in y direction that C moves during time increment Δt =
vΔt
Net displacement in y direction of C relative to A =
vΔt

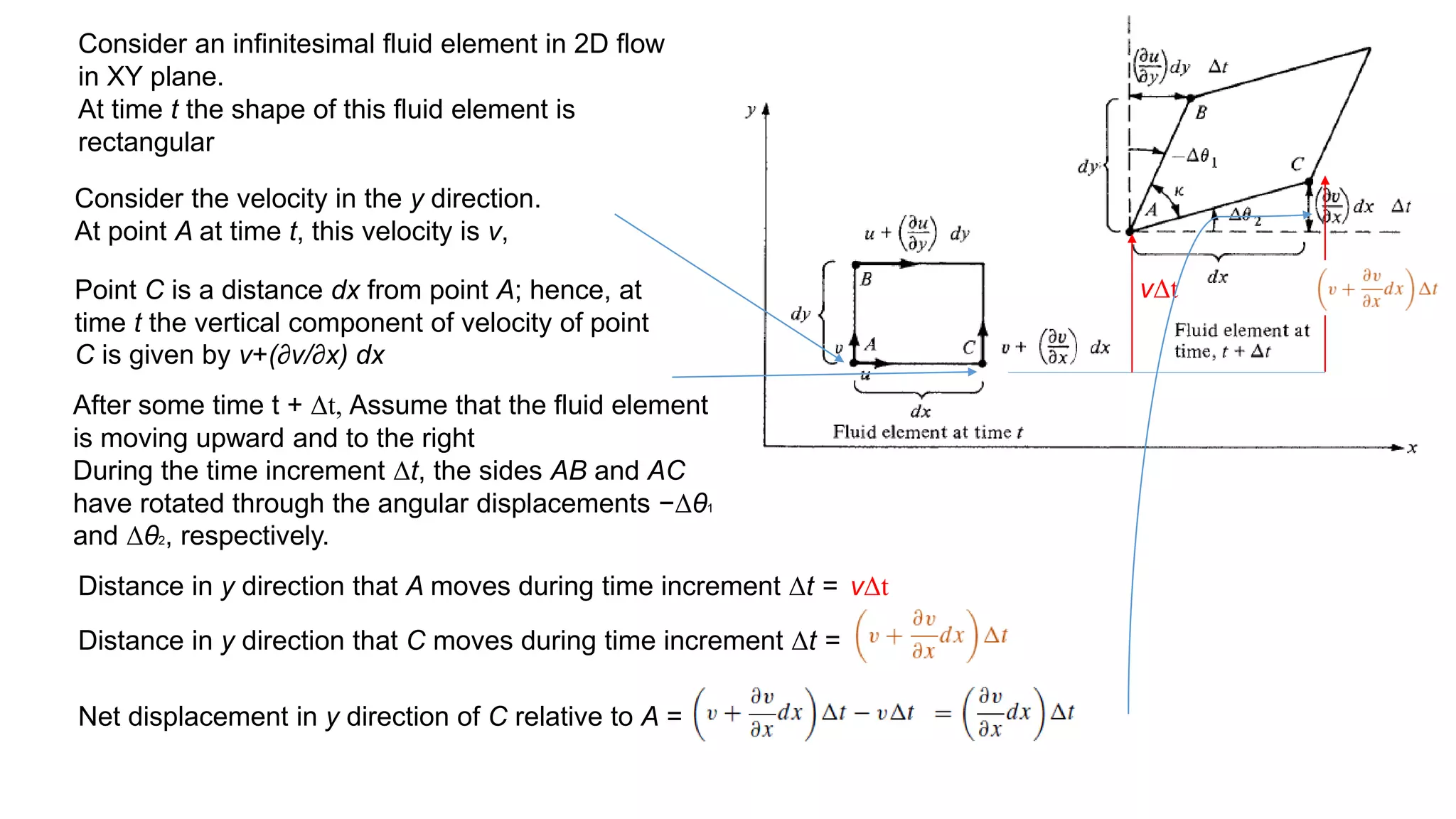
36. From the geometry
Since Δθ2 is a small angle, tan Δθ2 ≈ Δθ2. Hence,
Now consider line AB
The x component of the velocity at point A at time
t is u.
Because point B is a distance dy from point A,
the horizontal component of velocity of point B at
time t is u + (∂u/∂y) dy.
uΔt
the net displacement in the x direction of B relative to A over the time increment Δt =
[u+(∂u/∂y)dy]Δt
[(∂u/∂y)dy]Δt
From the geometry
Since −Δθ1 is small,

37. Consider the angular velocities of lines AB and AC, defined as dθ1/dt and dθ2/dt, respectively.
By definition, the angular velocity of the fluid element as seen in the xy plane is the average of the angular
velocities of lines AB and AC.
The fluid element is generally moving in three-dimensional space, hence the angular velocity of the fluid
element in three-dimensional space is

38. Vorticity
which is simply twice the angular velocity.
Consider the velocity field in Cartesian coordinates.
Curl of a Vector Field can be given as
Where u, v, and w denote the x, y, and z components of velocity, respectively,
In a velocity field, the
curl of the velocity is
equal to the vorticity.
1. If at every point in a flow, the flow is called rotational.
i.e the fluid elements have a finite angular velocity.
2. If ∇×V = 0 at every point in a flow, the flow is called irrotational.
i.e the fluid elements have no angular velocity

39. Fluid elements when Fluid elements when ∇×V = 0
the strain of the fluid element in the xy plane is the change in κ,
where positive strain corresponds to a decreasing κ.
Strain
the time rate of strain is

40. CIRCULATION
Consider a closed curve C in a flow field.
Let V and ds be the velocity and directed line segment, respectively, at a point on C.
The circulation,
Circulation is also related to vorticity
the circulation about a curve C is equal to the vorticity
integrated over any open surface bounded by C.

41. STREAM FUNCTION (ψ)
Consider two-dimensional steady flow, the differential equation for a streamline is
If u and v are known functions of x and y, then above equation can be integrated to yield the algebraic equation
for a streamline:
where c is an arbitrary constant of integration, with different values for different streamlines.
let
= mass flow between the two streamlines.
the mass flow between two streamlines is per unit depth perpendicular to the page.
the mass flow inside a streamtube bounded by streamlines ab and cd,
with a rectangular cross-sectional area
derivatives of ψ yield the flow-field velocities.

42. Assume the streamlines are close together (i.e., assume Δn is small), such that the flow velocity V is a
constant value across Δn.
The mass flow through the streamtube per unit depth perpendicular to the page is
Apply the limit as Δn → 0

43. Due to conservation of mass, the mass flow through Δn (per unit depth) is
equal to the sum of the mass flows through Δy and − Δx (per unit depth)
Letting cd approach ab,
For incompressible flow
the dimension of is equal to mass flow per
unit depth
In polar coordinates
In Cartesian coordinates
Assuming that ψ(x, y) is known through the 2D
flow field, then:
1. ψ = constant) gives the equation of a
streamline.
2. The flow velocity can be obtained by
differentiating ψ

44. VELOCITY POTENTIAL
Consider an irrotational flow, where the vorticity is zero
Consider the following vector identity: if φ is a scalar function, then
The curl of the gradient of a scalar function is identically zero.
For an irrotational flow, there exists a scalar function φ such that the velocity is given by the gradient of φ. And
φ is called Velocity potential.
φ is a function of the spatial coordinates; that is, φ = φ(x,y, z)
In polar coordinates
Assuming that φ(x, y, z) is known through the 3D
flow field, then:
1. Line of constant φ is an equipotential line.
2.The flow velocity can be obtained by
differentiating φ

45. The differences between φ and ψ
The velocity potential φ The stream function ψ
The flow-field velocities are obtained by
differentiating φ in the same
direction as the velocities
The flow-field velocities are obtained by
differentiating ψ normal to the velocity direction
The velocity potential is defined for irrotational
flow only.
The stream function can be used in either
rotational or irrotational flows.
The velocity potential applies to three-
dimensional flows
The stream function is defined for two-
dimensional flows only

46. RELATIONSHIP BETWEEN THE STREAM FUNCTION AND VELOCITY POTENTIAL
Consider a two-dimensional, irrotational, incompressible flow in Cartesian coordinates.
For a streamline, ψ(x, y) = constant. then
We know that
Solve this equation for dy/dx, which is the slope of the ψ = constant line(streamline)
Similarly, for an equipotential line, φ(x, y) = constant.
We know that
Solving equation for dy/dx, which is the slope of the φ = constant line (equipotential line)
streamlines and equipotential lines are mutually perpendicular

47. Uniform flow Sink flow
Source flow