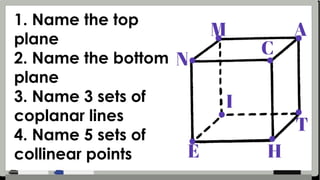
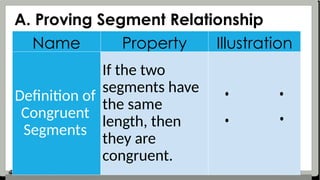
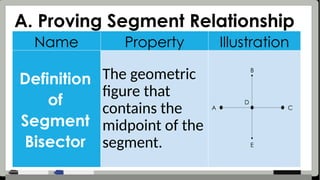
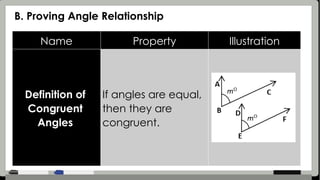
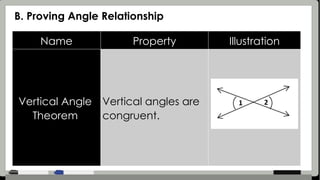
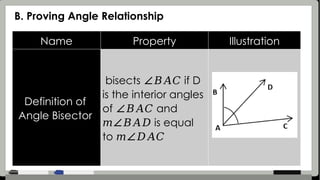
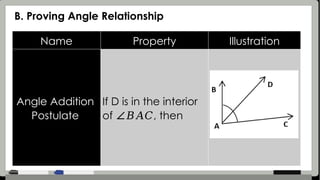
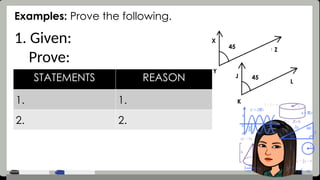
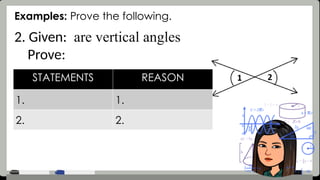
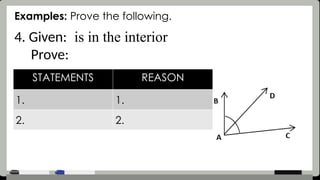
The document provides detailed assessment directions for geometric proofs, requiring students to identify planes, lines, points, and relationships such as congruence and bisectors. It outlines key properties, definitions, and postulates related to segments and angles, alongside examples of proofs that students must complete. The focus is on applying geometric concepts and logical reasoning to demonstrate understanding of segment and angle relationships.

1. Assessment #1

2. Directions: Give what is
asked in the following
conditions. Write your
answer in 1/2 crosswise.
(2 points each)

3. 1. Name the top
plane
2. Name the bottom
plane
3. Name 3 sets of
coplanar lines
4. Name 5 sets of
collinear points

4. Congruent
Segments and
Angles

5. A. Proving Segment Relationship
Name Property Illustration
Definition of
Congruent
Segments
If the two
segments have
the same
length, then
they are
congruent.

6. Name Property Illustration
Definition of
Midpoint
If a point on the
segment equidistant
from the two
endpoints of the
segment, then the
point is the midpoint of
the segment.
A. Proving Segment Relationship

7. Name Property Illustration
Definition
of
Segment
Bisector
The geometric
figure that
contains the
midpoint of the
segment.
A. Proving Segment Relationship
D
A C
B
E

8. Name Property Illustration
Segment
Addition
Postulate
If a point X is
between points P
and Q which are
collinear, then
A. Proving Segment Relationship

9. Examples: Prove the following.
1.Given: EF = GH
Prove:
STATEMENTS REASON
1. 1.
2. 2.

10. Examples: Prove the following.
2. Given: F is the midpoint of
Prove:
STATEMENTS REASON
1. 1.
2. 2.
𝐸 𝐹

11. Examples: Prove the following.
3. Given: Line GI bisects
Prove:
STATEMENTS REASON
1. 1.
2. 2.
J
F H
G
I

12. Examples: Prove the following.
3. Given: Line GI bisects
Prove:
STATEMENTS REASON
1. Line GI bisects 1. Given
2.
2. Def. of
Segment Bisector
J
F H
G
I

13. Examples: Prove the following.
4. Given: B is the midpoint of Prove
STATEMENTS REASON
1. 1.
2. 2.
𝐴 𝐵

14. Name Property Illustration
Definition of
Congruent
Angles
If angles are equal,
then they are
congruent.
B. Proving Angle Relationship

15. Name Property Illustration
Vertical Angle
Theorem
Vertical angles are
congruent.
B. Proving Angle Relationship

16. Name Property Illustration
Definition of
Angle Bisector
bisects if D
∠𝐵𝐴𝐶
is the interior angles
of and
∠𝐵𝐴𝐶
is equal
𝑚∠𝐵𝐴𝐷
to 𝑚∠𝐷𝐴𝐶
B. Proving Angle Relationship

17. Name Property Illustration
Angle Addition
Postulate
If D is in the interior
of , then
∠𝐵𝐴𝐶
B. Proving Angle Relationship

18. Examples: Prove the following.
1. Given:
Prove:
X
Y
Y
Z
J
K
L
45
45
STATEMENTS REASON
1. 1.
2. 2.

19. Examples: Prove the following.
2. Given: are vertical angles
Prove:
STATEMENTS REASON
1. 1.
2. 2.

20. Examples: Prove the following.
3. Given: bisects
Prove:
STATEMENTS REASON
1. 1.
2. 2.

21. Examples: Prove the following.
4. Given: is in the interior
Prove:
STATEMENTS REASON
1. 1.
2. 2.