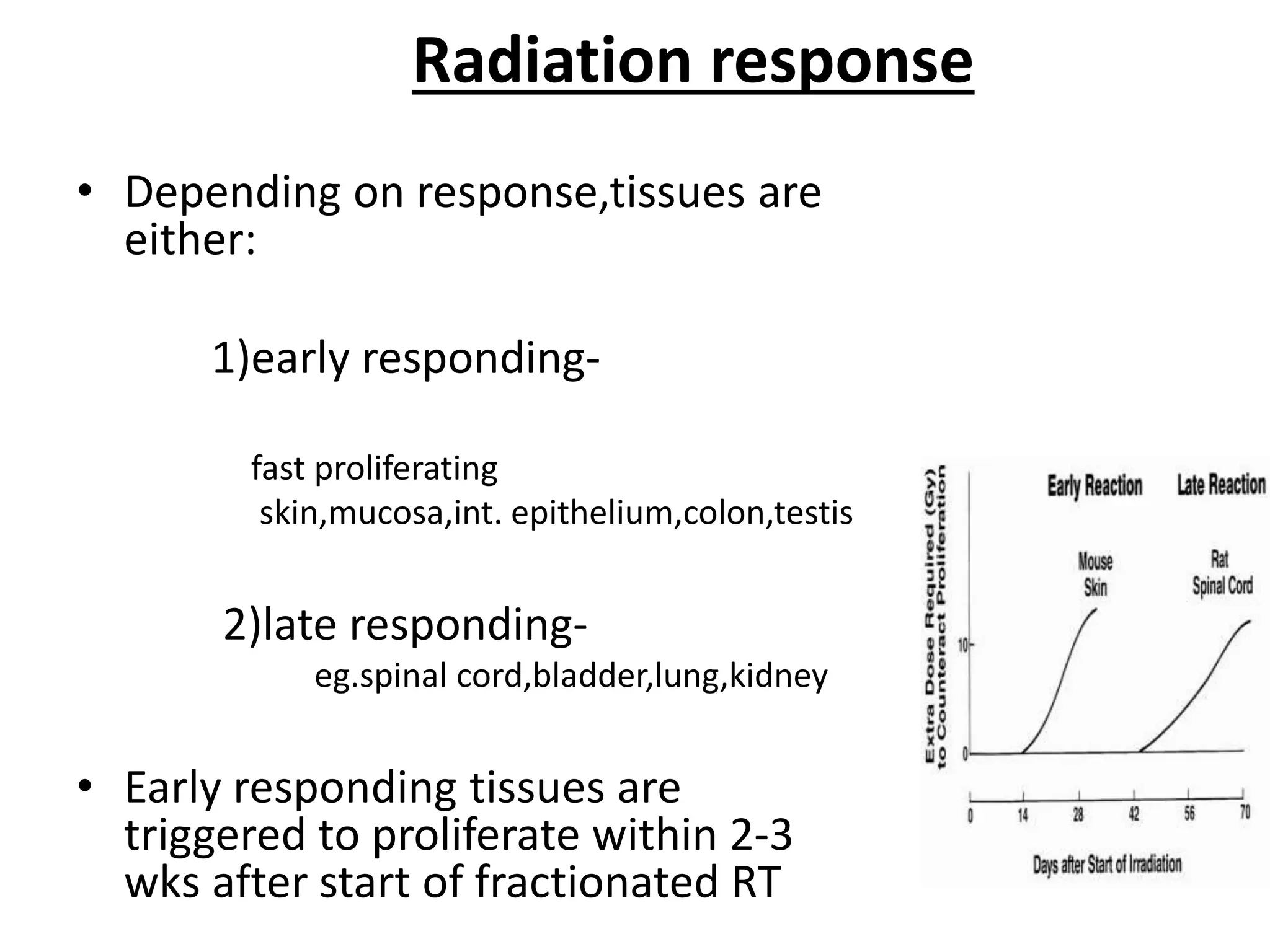
Fractionation involves dividing the total radiation dose into smaller daily fractions over the treatment period. This allows normal tissues to repair sublethal damage between fractions better than tumor tissues. Historical models like Stranquist cube root and Cohen's models related total dose and treatment time to biological effects. The linear quadratic model explains cell survival based on linear and quadratic components of radiation damage. Fractionation takes advantage of the four R's of radiobiology: repair of sublethal damage, repopulation, reoxygenation, and redistribution to improve the therapeutic ratio and deliver tumoricidal doses with minimal damage to surrounding normal tissues.

1. FRACTIONATION
-HISTORY
-RATIONALE
-CONCEPTS
Dr AMALU AUGUSTINE
Dept of Radiation oncology
GOVT MEDICAL COLLEGE
THIRUVANANTHAPURAM

2. • Definition
• History
– TDF models
• Stranquist
• Cohens
• Fowler
• Ellis
• Target model
– LQ model
• BED
• R’s of radiobiology
• Conventional fractionation

3. Fractionation
division of total dose of radiation into a no. of
separate fractions over total treatment time
– To deliver precisely measured dose of radiation
to a defined tumor volume
– with minimal damage to surrounding normal
tissue.

4. Historical review
• From the very beginning of RT , treatments
were fractionated
• X-ray
– just 1 month after its discovery
– Emil Grubbe(1896)
• Carcinoma breast
• 18 daily 1 hr #s
– Forced to use fractionated regime because of
low output from early Xray machines

5. • Single fraction radiotherapy -in
1914
• advent of Coolidge hot
cathode tube, with
– high output,
– adjustable tube currents &
–reproducible exposures
• The following ten years was a
period of uncertainty , about the
proper ways to fractionate.

6. ErIangen school ( Germany)
• Wintz
• Advocated single RT
• Fractionation allow tumor cells
time for recovery
• BERGONIE TRIBONDEAU LAW
– Rapidly growing tumor cells -
metabolically more active-
– Better able to recover from injury-
– will favor tumor cells if the
tumoricidal dose is not applied in the
first treatment.
Paris school ( France)
•Used radiobiological
principles of Regaud
• The Ram
experiment(1920’s)

8. Single dose of X-rays
• extensive scrotal skin
damage
Same dose in multiple #s
• sterilisation, no skin
damage
Tumour Normal
tissue

9. • HENRI COUTARD-1932
• Curie institute,Paris
• FRACTIONATION OF RADIATION PRODUCED
BETTER TUMOR CONTROL FOR A GIVEN LEVEL OF
NORMAL TISSUR TOXICITY THAN A SINGLE LARGE
DOSE.

10. Time ,Dose , Fractination Models
• With introduction of various fractionation schemes
– need for quantitative comparisons of treatments was felt
– to optimize treatment for particular tumor.

11. • Importance of tdf models
• 1. to calculate new total dose required to keep
biological effectiveness when conventional
fractionation is altered.
• 2. to compare diff treatment techniques that
differ in no of #, dpf, and overall treatment time.
• 3. To strive for optimal fractionation regimen.

12. • Strandquist -
• Cube root model- 1944
– first to device scientific
approach
– for correlating dose to
overall treatment time
– to produce an equivalent
biological isoeffect
– Isoeffect curves are a set of
curves which relate total
dose to overall treatment
time for definite effects of
radiation

13. • Stranquist plot / Cube root model
• relation between total dose & overall
treatment time
• He demonstrated that
– isoeffect curves (i.e. dose vs. no. of #s to
produce equal biological effect)
– on log-log graph
– for skin reactions (erythema & skin
tolerance)
– were straight lines with a slope of 0.33 i.e.

14. COHEN’S (1960)
• Cohen analyzed
– three diff. set of data
• erythema, skin damage and tumor control
• were documented for treatment times
from 1 to 40 days.
• Isoeffect curve for tumor control had a
smaller slope, m=0.22.
• Cohen found an exponent of
– 0.33for skin erythema / skin tolerance &
– 0.22 for skin cancers.

15. • According to Cohen’s results
– relationship b/w total dose & overall treatment time for normal tissue
tolerance & tumor can be written as
• Dn = K1 T.33
• D
t= K2 T.22
– K1& K2 are proportionality constants.
– Dn, Dt &T are normal tissue tolerance dose , tumor lethal dose & overall treatment
time respectively
• 0.33& 0.22 -> the repair capabilities
– of normal tissue & tumor cells respectively.
• This means as the treatment time is increased, tumor control
comes closer to the maximum tolerated skin dose.
• i.e. Tumor control can be achieved with , less normal tissue
damage.

16. Fowler
• Difference in exponents of time factor in Cohen’s formulations
– indicate that repair capacity of normal tissue is larger than that of tumor
• Fowler
– studies on pig skin
– showing normal tissue have two type of repair capabilities
• Intracellular
• having short repair half time of 0.5 to 3hrs &
• is complete within few hrs of irradiation.
• multiplicity of completion of recovery is equal to no. of #s.
• Homeostatic recovery - takes longer time to complete
• Hence no. of #s are more important than overall t/t
• This led Ellis to formulate NSD

17. NSD MODEL
Cube root law was the result of biological effect that were functions of
N and T
• time factor was a composite of
N (no. of #s) &
T (overall treatment time)
• Exponents for
– intracellular -0.22
– homeostatic recovery - 0.33-0.22=0.11
• Frank Ellis, British, 1969
• Fractionation is twice as important as time according to clinical
observations

18. • Hence dose is related to time & no. of #s as
D =NSD X T .11 X N.24
• This correlated well with Strandquist’s data.
– i.e. For treating once a day, everyday. T0.11 x T0.24 = T0.35.
• By not treating on weekends this will be reduced to T0.33
– The constant NSD is Nominal Standard Dose.
• NSD is a constant of proportionality
• which can be thought of as a bioeffective dose
• i.e. dose corrected for time and fractionation.
• NSD= D. T-0.11 .N-0.24
• Unit of NSD is RET ( Roentgen Equivalent Therapy)
• NSD can be used to compare two fractionation regimes.

19. Clinical use
• Enable clinicians to change from one
fractionation regimen to another,
– while maintaining equivalent biological effects on
both tumour and normal tissues
• Limitation:-
– omitted the importance of dose per fraction in
determining late effects in normal tissues

20. • Limitaitions of Elllis
• Was based on
• early Xray damage to skin &
• for trtmt upto 6 weeks.
• So cannot be applied for:
• 1.Late effects.
• 2.For other normal tissue effects that limit maximum dose.
• 3.For n<4
• 4.For high LET radiation.
• 5.Does not allow for explanation of important differences btw early and late
effects in fr. RT.

21. TDF
• Ortan & Ellis (1973)
• Basic formula of NSD is
– NSD = D x T-0.11 x N-0.24
– Replacing
• D= Nd (where N– no. of #s & d – dose/#)
• NSD = Nd x (T /N) -0.11 x N -0.24
• Raising both side of equation to power 1.538
• TDF = 1.19 Nd 1.54 (T/N) -0.17

22. • TDF contd.
• Allowance must be made for repopulation during rest period or
break
• According to Ellis,
– TDF before break should be reduced by decay factor to calculate
TDF after break
• Decay factor = {T/ (T+R)}.11
• T= time from beginning of RT to break.
• R= rest interval in days.

23. • TDF factor is derived from the basic NSD equation.
• TDF tables are available for rapid solution of NSD
problem.
• In split course regimes, overall effect= sum of TDF
factors
• TDF1 . [T/T+R]0.11 + TDF2

24. CRITICISMS OF NSD
• Do not take into account complex biological processes that take place
during or after irradiation
• Values of exponent of N in NSD eq. are not same for diff. tissue types.
• Validity of NSD w.r.t. different effects in same tissue is doubtful.
– For late effects in skin, the influence of no. of #s may be considerably
larger than for acute skin responses
• Uncertainty relates to no. of #s for which formula provides reasonable
approximation of tolerance dose of a given tissue.
– For effects in skin , approximation is obtained b/w 10 to 25 #s

25. SINGLE HIT SINGLE TARGET THEORY
• Crowther & expanded by Lea
• Single hit is sufficient to produce measured effect
or to inactivate a cell
• To express relationship b/w no. of cells killed &
dose delivered in mathematical terms
• The curve is exponential
– i.e. at low doses the relationship is linear & as
process continues larger doses are required to
inactivate same no. of organisms.
S = e –p
p= D / D0
S = e –(D/D0)
• Where 1/Do is constant of proportionality

26. • Where Do is the mean lethal dose that will produce avg. one
hit per cell
• such log survival curve is linear showing Do as dose that reduce
cell survival fraction to 37%
• Such curves are observed in mammalians cells only
– When cell are irradiated with
• high LET radn e.g. α - particles
• are synchronized in most sensitive phases of cell cycle (lateG2 or M)

27. MULTITARGET SINGLE HIT THEORY
• According to this theory some organisms
contain more than one target & to inactivate
organism each target should receive one hit
• Survival curves corresponding to this theory
start with less sensitive region at low doses &
show exponential behavior at large doses i.e.
curves show a shoulder region in the
beginning.
• Such curves are observed when mammalian
cells are irradiated with low LET radn e.g. x-
rays
• Shoulder represents cells in which fewer than
n targets have been damaged after receiving a
dose D i.e. cells have received SLD which can
be repaired.

28. • Radiation induced cell killing:2 components
1. Cell kill proportional to dose {initial slope(α)}
2. Cell kill proportional to square of dose {final slope(β)}
• LQ model
– explain the dose response of exchange type
chromosomal aberrations resulting from 2 separate
breaks in the chromosomes
– Currently also used to explain the shouldered survival
curves

29. LINEAR QUADRATIC MODEL
• Basis of LQ theory is that cell is damaged when both strands of
DNA are damaged.
• This can be produced either by single ionizing particle i.e.
E= αD
S= e –αd
– Where α is constant of proportionality
– Or it can be accomplished by independent interaction by
two separate ionizing particles such that
» E ∞ D2
» E= βD2
» S= e –(βD2)
• Overall LQ eq. for cell survival is therefore
• S= e (–αD – βD2)

30. • Linear component(α)
irreparable damage
• Quadratic component (β
reparable damage
• α/βcurviness of cell
survival
• Higher αstraighter curve
• At a particular
dose,D=α/β,both
components equal

31. • D= α / β
– is the dose at which log of surviving # for α-
damage equals that for β- damage.
• α / β represents curviness of cell survival curve.
– Higher the α / β,
• straighter is the curve &
• cells show little repair of SLD
– low α / β
• high capability of repair.
• Tumor
– high α / β values in range of 5-20Gy (mean
10Gy)
• late responding normal tissue
– α / β in range 1-4Gy (mean 2.5Gy)

32. Radiation response
• Depending on response,tissues are
either:
1)early responding-
fast proliferating
skin,mucosa,int. epithelium,colon,testis
2)late responding-
eg.spinal cord,bladder,lung,kidney
• Early responding tissues are
triggered to proliferate within 2-3
wks after start of fractionated RT

33. Dose response :early vs late
Early responding
• Curve –less curved
• Less level of SLD
repair
• Low β
• High α/β
• Highly sensitive to
dose delivered/#
Late responding
• More curved
• More repair
• Higher β
• Lower α/β
• Sensitive to total
dose,not dose/#
Linear and quadratic components of
cell killing are equal by about 2 Gy

34. Why diff in response?
Cells may be radioresistant in two diff situations:-
• 1)Popln proliferating so
slow that most cells are in
G1 phase/not
proliferating at all(G0
phase)
• Quadratic(β) cell killing
predominates
• Such resistance
disappears at high dose/#
• So,late responding tissues
are highly affected by
dose/# rather than total
dose
• Proliferation so fast-S
phase occupies a major
portn
• Linear(α) cell killing more
predominates
• Fraction size &overall
treatment time are
important

35. • NSD & TDF models are empirical models while LQ
model is derived from cell survival curves.
• LQ model is based on fundamental mechanism of
interaction of radiation with biological systems.

36. Biological effective dose(BED)
• Barendsen
• Jack Fowler
• quantity by which diff. fractionation regimens are
intercompared
• Where
• n - no. of #s
• d - dose/#

37. RADIOBIOLOGICAL RATIONALE FOR FRACTIONATION
• Delivery of tumorocidal dose in small dose fractions in conventional
multifraction regimen is based on 4R’s of radiobiology namely
• 4 R’s of radiobiology(Withers-1975)
Repair
Reassortment
Repopulation
Reoxygenation
5th R Radiosensitivity
6th R – Remote bystander effect

38. Repair of sublethal damage
• Most important ‘R’
• Most important rationale for fractionation
• Mammalian cells can repair radiation damage in b/w dose
fractions.
• complex process –
– repair of SLD by a variety of repair enzymes & pathways.

39. Radiation induced damage:
• Lethal-
• irreversible, irreparable & leads to cell death
• Potentially lethal-
• can be manipulated by repair when cells are allowed to remain
in non-dividing state.
• Sublethal-
• repaired in hrs, unless additional SLD is added to it

40. • Tumerocidal doses are very high as compared to NTT
– two ways to deliver such high doses:
1. to deliver much higher dose to tumor than to normal tissue –
basis of conformal radiotherapy
2. to fractionate the dose.
• sufficient time b/w consecutive fractions
• for complete repair of all cell that suffered SLD during 1st #
before 2nd #& so on
– small dose /#
• spares late reactions preferentially
– a reasonable schedule duration
• allows regeneration of early reacting tissues.

41. Split dose expt
• demonstrated by Elkind & Sutton
• Single dose-15.58 Gy SF 0.005
• 2 doses split by interval 30 min
• SF increases as time interval b/w
doses is incr until 2 hrs0.02
• Further increase in time
interval no advantage

42. Mechanism of SLD repair
• DS breaks produced after 1st dose are rejoined and
repaired before 2nd dose
• Extent of SLD repair vary with type of radiation
– Higher for X rays fractionation marked inc. in cell survival
• Initiated within seconds of injury,complete within 6 hrs
• Repair is an active process requiring o₂,nutrients

43. How it helps?
• Advantageous to normal tissues,
– as they are able to repair radiation
damage better than that of tumour
cells

44. Redistribution
• Increase in survival during 1st 2hrs in
split dose experiment results from
repair of SLD
• If interval b/w doses is 6hrs then
– resistant cells move to sensitive
phases
– increases cell kill in fractionated
treatment relative to a single session
treatment.
• Cells are
– sensitive during M & G2 phase
– resistant during S phase of cell cycle .

45. Reassortment
non-cycling cells recruited
into the cycling pool
Reassortment
replacement by cells from
less sensitive parts of cycle
(within two cycles )
Cells killed in sensitive
phases
leave a gap in the cell population
•‘movement of cells through
the cell cycle during the
interval between the split
doses’.
•Benefit : if tumour cells are
caught in the radiosensitive
phase of cell cycle after each
fraction.

46. • Asynchronous population of cells
irradiated
• more cells are killed in sensitive
phase
• surviving fraction of cells partly
synchronized(in radioresistant S
phase)
• In the next 6 hrs,the surviving cells
move through the cell cycle and
reach sensitive phase
• killed by2nd dose

47. Repopulation
• In b/w dose fractions normal cells as well as tumor cells
repopulate.
– difficult it becomes to control tumor & may be detrimental
• acutely responding normal tissue need to repopulate during
course of radiotherapy .
• fractionation must be controlled so as
– not to allow too much time for excessive repopulation of tumor
cells
– at the same time not treating so fast that acute tolerance is
exceeded

48. • If the total dose is delivered in 2 #s
separated by a time interval,
– there is increase in cell survival
• In a rapidly div cell,after the first 2 hrs,
– there is a dip in survival
(reassortment)
• If time interval b/w split doses exceed
cell cycle,
– there is an increase in
survival(repopulation)

49. Repopulation
•Tissues with large clonogenic populations do
better
• Rapid repopulation may reduce level of repair

50. ACCELERATED REPOPULATION
• Treatment with any cytotoxic agent , including
radn
– triggers surviving cells (clonogens) in a tumor
to divide faster than before
• tumour regressing -> clonogens rapidly
dividing
• Wither and colleagues-
– clonogen repopulation in human H&N cancer
accelerates at 28 days after start of
fractionated regime
• Implication
– 1)treatment to be completed as soon as it is
practicable
– 2)Better to delay start of treatment than to
introduce gaps in b/w

51. Reoxygenation
• center of tumor
– hypoxic
– resistant to low LET radiation.
• Hypoxic cells get reoxygenated
– occurs during a fractionated course of treatment,
– making them more radiosensitive to subsequent doses
of radiation.

52. Oxygen enhancement ratio(OER)
• The ratio of doses administered
under hypoxic to aerated
conditions needed to achieve the
same biological effect
• Sparsely ionising radiation(X-
rays)-OER 2.5-3.5 @high doses
• Slightly lower 2.5@ low doses

53. Oxygen effect is of great importance in sparsely ionising radiation
e.g,X-rays,intermediate value for fast neutrons and absent for
densely ionising radiation eg:α particle

54. HYPOXIA
1)Acute-
temporary closure of bv d/t
malformed vasculature
2)chronic-
d/t ltd diffusion distance of
oxygen through respiring tissue
Most tumors >1 cm have some
hypoxic cells in them
Some tumor types have larger %
Major contributor to tumor
radiation resistance.

55. Reoxygenation
• Mixed population of aerobic
& hypoxic cells
• Irradiated -preferential killing
of aerated cells
• Resulting popln-mainly
hypoxic cells
• If sufficient time allowed
before next dose,the process
of reoxygenation restores the
proportion of hypoxic cells
back to 15%

56. Mechanism of reoxygenation
• as cells killed by radiation are broken down
• Restructuring/revascularisation of tumors
• tmr shrinks in size
• cells beyond the range of oxygen diffusion previously
become closer to a bld supply(days)

57. • Radiosensitivity
• Radiosensitivity expresses the response of the tumor
to irradiation.
• Bergonie and Tribondeau:
– RS will be greater if the cell:
• Is highly mitotic.
• Is undifferentiated.
• Has a high carcinogenetic feature.
• Malignant cells have greater reproductive capacity
hence are more radiosensitivity

58. though tumors are
more sensitive,
therapeutic ratio is
low.
NTT exceeds TLD by
only small #.
e.g. sq. cell. ca. &
adenoca.
Skin, Mesoderm
organs (liver, heart,
lungs…)
• Therapeutic ratio is
high
• Normal tissue tolerates
doses several times
magnitude of TLD.
• e.g. lymphoma,
leukemia,seminoma
• ,dysgerminoma ,
• Bone Marrow, Spleen,
Thymus ,Lymphatic
nodes,Gonads,Eye lens,
Lymphocytes
(exception to the RS
laws)
• Dose required to
produce lethal
effect is more
than NTT.
• Hence therapeutic
index is very low.
• e.g. soft tissue &
bone sarcoma,
melanoma etc.
• Muscle, Bones,
Nervous system
Highly radiosensitive Moderately sensitive Resistant

59. • 6 th R - remote bystander effect
• Non irradiated cells that are located near the
irradiated cells undergo damage similar to that of
irradiated cells.
• due to cellular communication through gap
junctions
• Occurs both in tumour cells and normal cells

60. Summary
fractionation
Spares normal tissues
• Repair of sublethal damage
in between dose fractions
• Repopulation of cells,if
sufficiently long time
Increases damage to tumour
• Reoxygenation
• Reassortment of cells into
radiosensitive phases of cell
cycle

61. ADV. OF FRACTIONATION
• Acute effects of single dose of radiation can be decreased
• Pt.’s tolerance improves
• Exploits diff. in recovery rate b/w normal tissues & tumors.
• Radn induced redistribution & sensitization of rapidly
proliferating cells.
• Reduction in hypoxic cells leads to –
– Reoxygenation
– Reduction in no. of tumor cells with each dose #

62. Conventional fractionation
• 1.8-2 Gy/day
• 5 days/week
• Total dose b/w 60-70 Gy for gross solid
tumour

63. • Evolved as conventional regimen because it is
• Convenient (no weekend treatment)
• Efficient (treatment every weekday)
• Effective (high doses can be delivered without exceeding
either acute or chronic normal tissue tolerance)
• Rationale for using conventional fractionation
• Most tried & trusted method
• Both tumorocidal & tolerance doses are well documented

64. THANK YOU