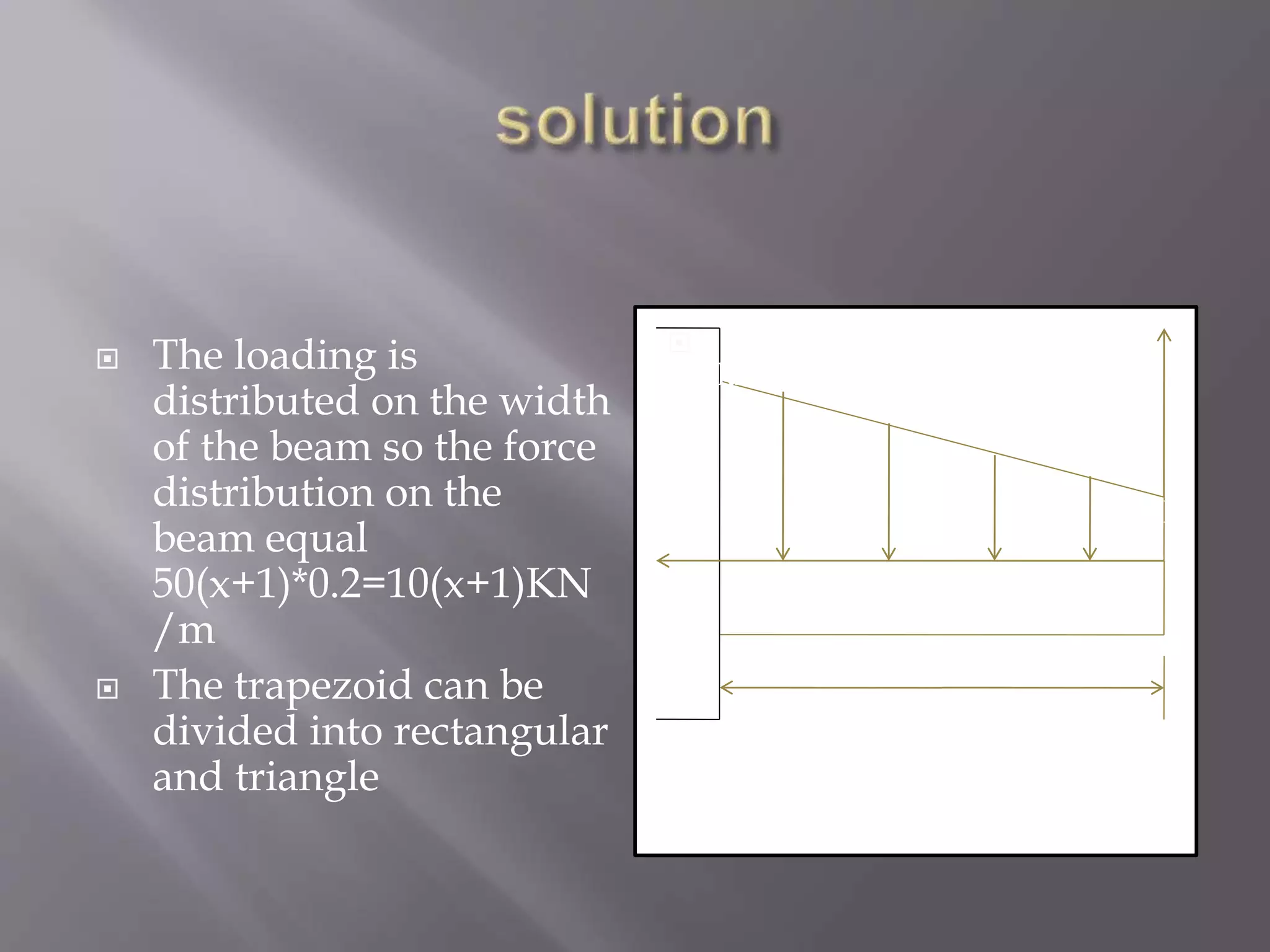
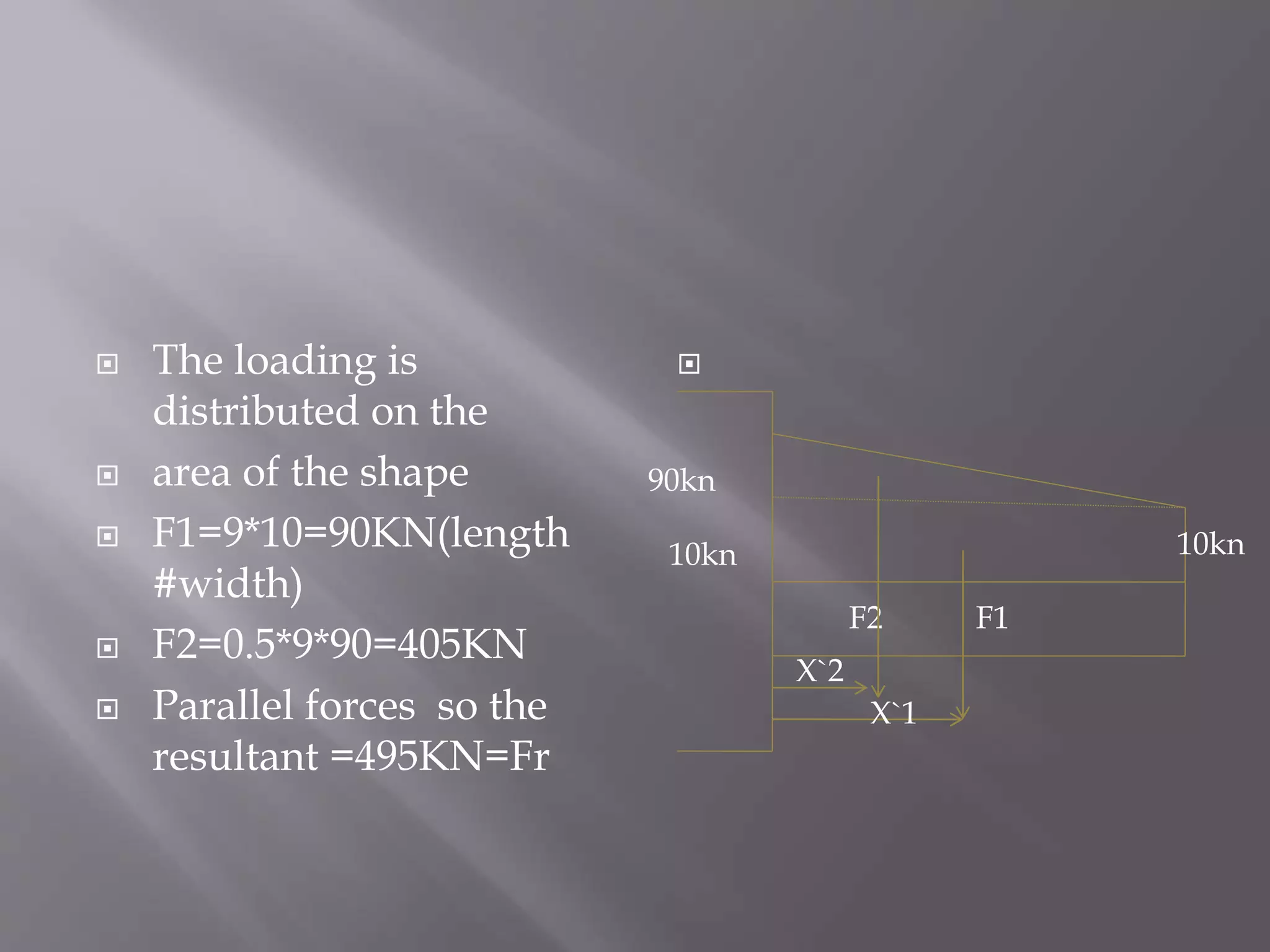
1) The document describes the steps to determine the equivalent resultant force of a distributed load on a beam, which includes: dividing the shape into known areas, determining forces on each area, and taking moments to find the location of the resultant force. 2) It then applies these steps to calculate the 495KN resultant force located at 3.27m for a trapezoidal distributed load varying from 50-100kPa on a 9m beam. 3) It also presents a problem to determine the resultant force for a distributed ground reaction loading of 0.5(1+cosα)KN/m around a pipe.

1.  We all see a rigid body on surface of something .this body has
material with special density so at least we study the weight force of
the body on the surface of the beam ;……etc.
 We start our study for the force of weight from :
 1#choosing axis for our problem at lowest height
 2#determining weight force at the beginning and the end of our
body/our axis(at X=0 at X has value)
 3#determining the force density for area
 4#divid the shape of the body into known shapes
 5#determinig centers of mass to all shapes
 6#determining the resultant of force according to the direction of
forces and taking the moment around any point .
 Remember this rule (moment of the resultant =summation of all
forces moments around point
 Notice :this steps to conclusive problem .some
problems does not need all these steps

2. SIMPLE DIAGRAM
 The granular material
exerts the distributed
loading 50(1+x)K pa on
the top surface of the
beam as shown in the
figure .determine the
magnitude and location
of the equivalent
resultant of this load

9m0.2m

3.  The loading is
distributed on the width
of the beam so the force
distribution on the
beam equal
50(x+1)*0.2=10(x+1)KN
/m
 The trapezoid can be
divided into rectangular
and triangle

9m
A B5
y
x
10kN
100kN

4.  The loading is
distributed on the
 area of the shape
 F1=9*10=90KN(length
#width)
 F2=0.5*9*90=405KN
 Parallel forces so the
resultant =495KN=Fr

F1F2
X`2
X`1
10kn10kn
90kn

5.  Note that X`2=3m X`1=4.5 m so he last thing to
know X`r
 MA=Fr*X`r=405*3 +90*4.5
 So the location of resultant force =3.27m

6.  if the distribution of the ground reaction on
the pipe (the diameter=1.6m )per meter of
length can be approximated as
(0.5(1+cosα)KN/m )shown figure .determine
the magnitude of the resultant force due to this
loading
0.5 KN/m
1K
N/
m