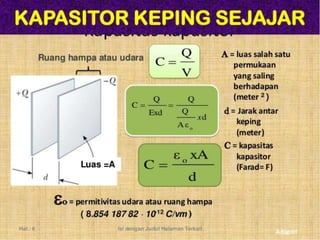
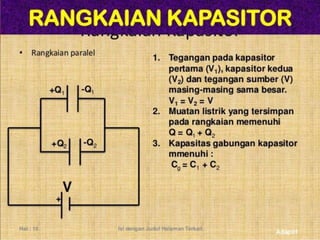
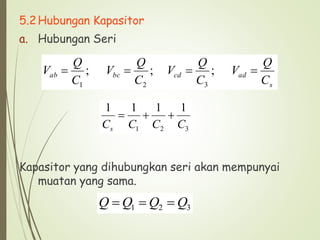
Dokumen tersebut membahas tentang: 1. Potensial listrik dan energi potensial listrik yang dihasilkan oleh muatan listrik 2. Kapasitor sebagai alat penyimpan muatan listrik dan faktor-faktor yang mempengaruhi kapasitasnya 3. Hubungan antara kapasitor yang dihubungkan secara seri dan paralel

1. Potensial Listrik & Kapasitor
Tryana -1012211055

2. Energi potensial listrik adalah usaha untuk memindahkan
muatan uji ke sekitar muatan sumber.
Dengan :
q = muatan sumber (C)
q’ = muatan uji (C)
Ep = energi potensial listrik (J)

3. Potensial Listrik
 Potensial listrik merupakan besar energi potensial tiap
satuan muatan.
 Karena potensial listrik adalah energi potensial
elektrostatik per satuan muatan, maka satuan SI untuk
beda potensial adalah joule per coulomb atau volt
(V). 1 V = 1 J/C
 Karena diukur dalam volt maka beda potensial
terkadang disebut voltase atau tegangan.

4. Dengan :
V = potensial listrik (J/C atau V)
q = muatan sumber (C)
r = jarak antar muatan sumber dan
muatan uji (m)

5. Potensial Listrik
Energi Potensial listrik  Energi yang diperlukan untuk memindahkan
Sebuah muatan ( “ melawan gaya listrik” )
Potensial Listrik  Energi potensial per satuan muatan  yang bisa di
ukur adalah beda potensial
Satuan Energi potensial  Joule
Satuan beda potensial  Volt

6. 𝑊𝐴𝐵 = ∆𝐸𝑝 = 𝐸𝑃𝐵 - 𝐸𝑃𝐴

7. Energi Potensial Listrik
Sebuah muatan uji q’ diletakkan di dekat muatan
sumber q, maka energi potensial yang dimiliki oleh
muatan uji q’ adalah
'
4
1
0 r
qq
Ep


+ r
q q’

8. Usaha untuk memindahkan muatan listrik
Usaha yang diperlukan untuk memindahkan sebuah
muatan uji q’ dari a ke b yang dipengaruhi oleh
muatan sumber q adalah
'
4
1
'
4
1
0
0 a
b
ab
a
b
ab
b
a
r
qq
r
qq
W
Ep
Ep
W
W








+ ra
q a
b
rb

9. Potensial listrik oleh muatan titik
Bila kuat medan merupakan besaran vektor, maka
potensial listrik merupakan besaran skalar. Muatan
positif akan menghasilkan potensial positif di
sekitarnya, sedangkan muatan negatif akan
menghasilkan potensial negatif.
4
1
0 A
A
r
q
V


4
1
0 B
B
r
q
V



+
-
rA
q A
B
rB
q

10. Sedangkan potensial listrik pada satu titik karena
pengaruh beberapa muatan listrik merupakan jumlah
aljabar dari masing2 muatan.
4
1
0


i i
i
r
q
V


11. X
Y
q1
q2
q3
P
𝑟3
𝑟2
𝑟
𝑟1
Tentukan potensial listrik pada titik
pengamatan P Yang berada pada posisi
i) Jarak muatan q1 ke titik P:
ii) Jarak muatan q2 ke titik P:
iii) Jarak muatan q3 ke titik P:𝑅3 = 𝑟 − 𝑟3
𝑅2 = 𝑟 − 𝑟2
𝑅1 = 𝑟 − 𝑟1
i) Potensial yang dihasilkan muatan q1
ii) Potensial yang dihasilkan muatan q2
iii) Potensial yang dihasilkan muatan q3
𝑉2 =
1
4𝜋ε𝑜
𝑞2
𝑅2
=
1
4𝜋ε𝑜
𝑞2
𝑟 − 𝑟2
𝑉3 =
1
4𝜋ε𝑜
𝑞3
𝑅3
=
1
4𝜋ε𝑜
𝑞3
𝑟 − 𝑟3
𝑉1 =
1
4𝜋ε𝑜
𝑞1
𝑅1
=
1
4𝜋ε𝑜
𝑞1
𝑟 − 𝑟1
𝑉 = 𝑉1 + 𝑉2 + 𝑉3

12. Kapasitor
 Kapasitansi kapasitor
 Kapasitor pelat sejajar
 Memperbesar kapasitansi kapasitor
 Kapasitor satu bola konduktor
 Kapasitansi dua bola konduktor konsentris
 Kapasitor dua silindris konsentris
 Kapasitor variable
 Rangkaian kapasitor

13. Kapasitor
 Kapasitor terdiri dari dua permukaan konduktor yang
dipisahkan oleh suatu bahan isolator yang disebut
sebagai dielektrik.
 Permukaan konduktor tersebut dapat berupa plat
berbentuk bulat atau persegi atau berupa silinder
atau bola.
 Kegunaan kapasitor adalah sebagai media
penyimpanan energi listrik dalam bentuk elektrostatis
dalam bahan dielektrik.

14. Kapasitansi kapasitor
 Sifat bahan yang mencerminkan kemampuannya
untuk menyimpan muatan listrik
V
q
C 
Keterangan :
q = muatan (C)
C = kapasitansi kapasitor (F)
V = besar tegangan (V)

18. 5.1 Pengertian Kapasitor
 Dua penghantar berdekatan yang dimaksudkan
untuk diberi muatan sama tetapi berlawanan jenis
disebut kapasitor.
 Sifat menyimpan energi listrik / muatan listrik.
 Kapasitas suatu kapasitor (C) adalah perbandingan
antara besar muatan Q dari salah satu
penghantarnya dengan beda potensial V antara
kedua pengahntar itu.

19. Kegunaan Kapasitor
 Untuk menghindari terjadinya loncatan listrik pada
rangkaian2 yang mengandung kumparan bila tiba2
diputuskan arusnya.
 Rangkaian yang dipakai untuk menghidupkan mesin
mobil
 Untuk memilih panjang gelombang yang ditangkap
oleh pesawat penerima radio.
Bentuk kapasitor
 Kapasitor bentuk keping sejajar
 Kapasitor bentuk bola sepusat
 Kapasitor bentuk silinder

20. 5.2 Kapasitas Kapasitor
Bila luas masing2 keping A,
maka :
Tegangan antara kedua
keping :
Jadi kapasitas kapasitor untuk ruang hampa adalah :
A
Q
E
0
0 




A
d
Q
d
E
V
0
.
.



d
A
V
Q
C 0
0 


+
+
+
+
+q -q
A
d
E
-
-
-
-

21. Bila di dalamnya diisi bahan lain yang mempunyai
konstanta dielektrik K, maka kapasitasnya menjadi
Hubungan antara C0 dan C adalah :
Kapasitas kapasitor akan berubah harganya bila :
K , A dan d diubah
Dalam hal ini C tidak tergantung Q dan V, hanya
merupakan perbandingan2 yang tetap saja. Artinya
meskipun harga Q diubah2, harga C tetap.
0
0 karena 
 K
KC
C 

d
A
K
C 0



22. 5.2Hubungan Kapasitor
a. Hubungan Seri
Kapasitor yang dihubungkan seri akan mempunyai
muatan yang sama.
3
2
1
1
1
1
1
C
C
C
Cs



3
2
1 Q
Q
Q
Q 


s
ad
cd
bc
ab
C
Q
V
C
Q
V
C
Q
V
C
Q
V 


 ;
;
;
3
2
1

23. b. Hubungan Paralel
Kapasitor yang dihubungkan paralel, tegangan antara
ujung2 kapasitor adalah sama, sebesar V.
3
2
1 C
C
C
Cp 


;
;
;
; 3
3
2
2
1
1 V
C
Q
V
C
Q
V
C
Q
V
C
Q p





24. 5.4 Energi Kapasitor
Sesuai dengan fungsinya, maka kapasitor yang
mempunyai kapasitas besar akan dapat
menyimpan energi yang lebih besar pula.
Persamaannya :
QV
CV
W 2
1
2
2
1



25. Contoh :
1. Tentukan kapasitas kapasitor yang mempunyai luas
keping 1 cm2 dan jarak antara kepingnya 0,2 cm,
bila muatan masing2 keping sebesar 5 μC dan ε0 =
8,85 x 10-12 C2/Nm2 dan diantara medium ada
bahan dengan konstanta dielektrik 2.
2. Suatu kapasitor keping sejenis mempunyai
kapasitas 5 μF, jika ruang diantara keping2 berisi
udara. Jika ruang tersebut diisi porselin,
kapasitasnya 30 μF. Berapakah konstanta
dielektrik porselin ?
3. Suatu kapasitor berisi udara, tegangannya V0.
Kapasitor itu kemudian diisi mika (K = 5) dan
diisolasi (muatannya dibuat tetap). Berapakah
tegangan kapasitor itu sekarang ?

26. 4. Tiga buah kapasitor dihubungkan secara seri dan
paralel, C1 = 1 μF, C2 = 2 μF, C3 = 3 μF dihubungkan
dengan sumber tegangan 12 V. Tentukanlah (a)
Kapasitas gabungannya, (b) muatan masing2
kapasitor.
5. Terdapat suatu rangkaian dengan 5 buah kapasitor
yang sama besarnya. Tentukan kapasitas antara
titik K dan M.
6. Jika sebuah kapasitor yang berkapasitas 10 μF
mempunyai energi listrik sebesar 1 Joule, maka
berapakah tegangannya ?