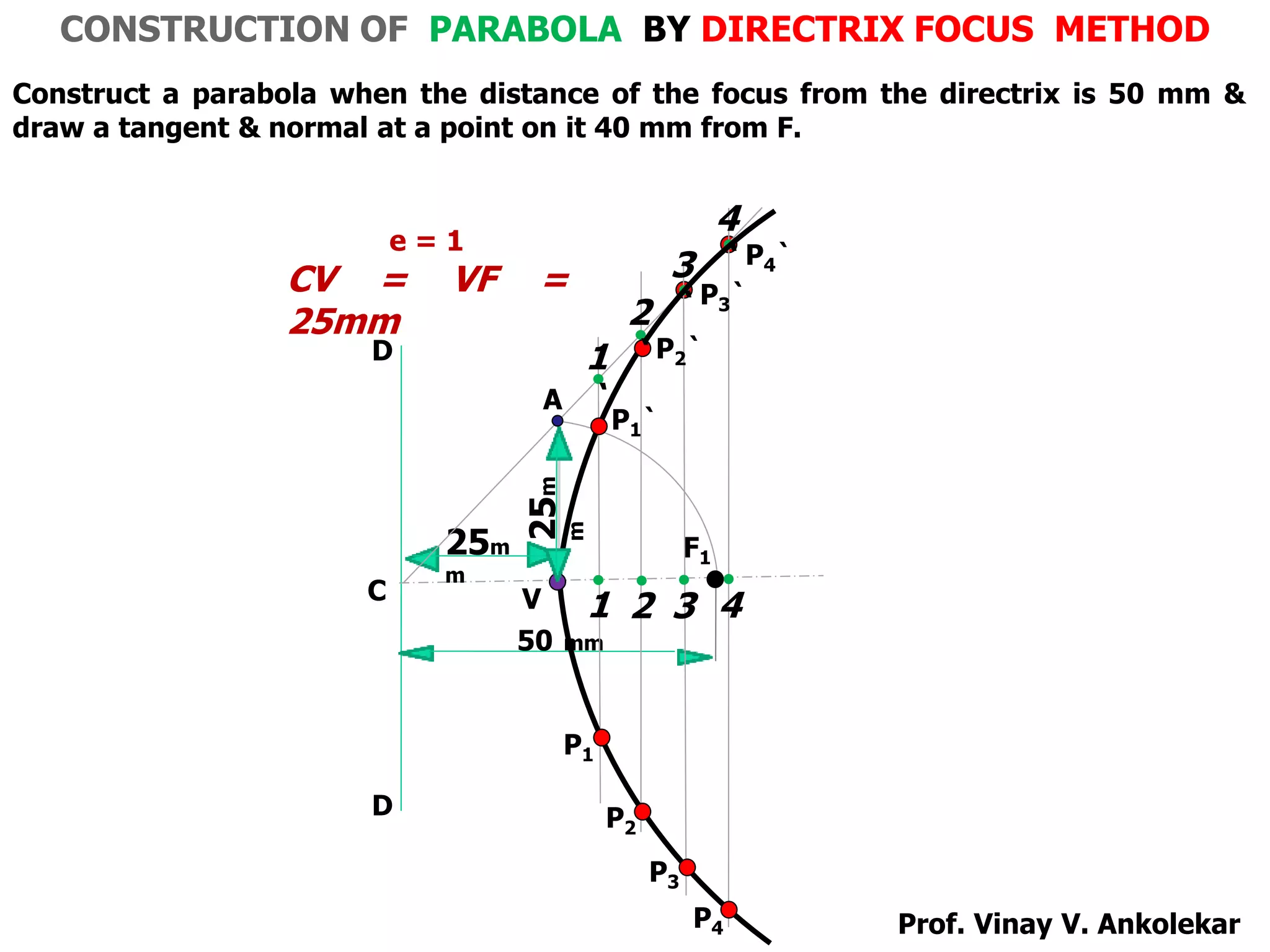
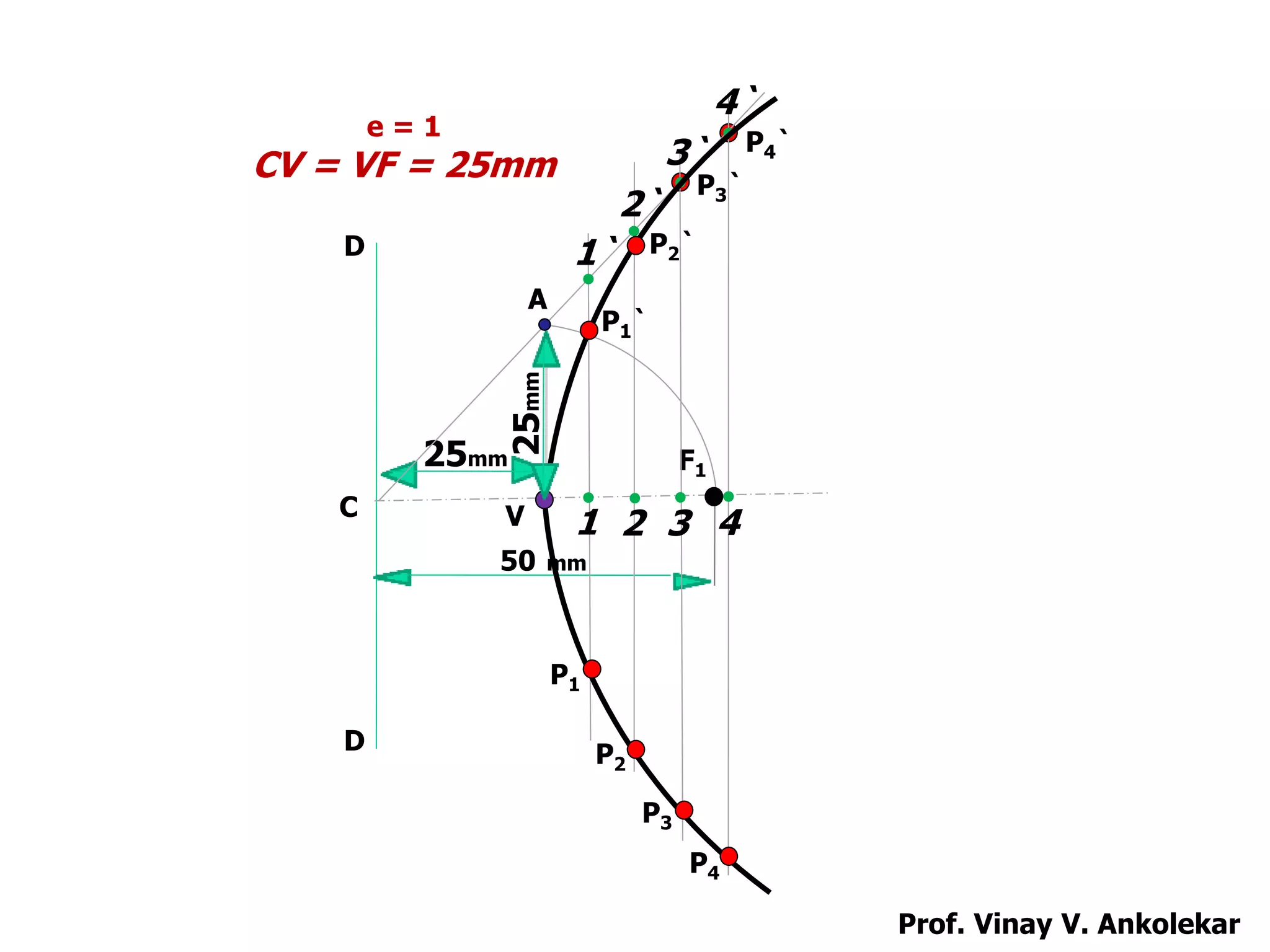
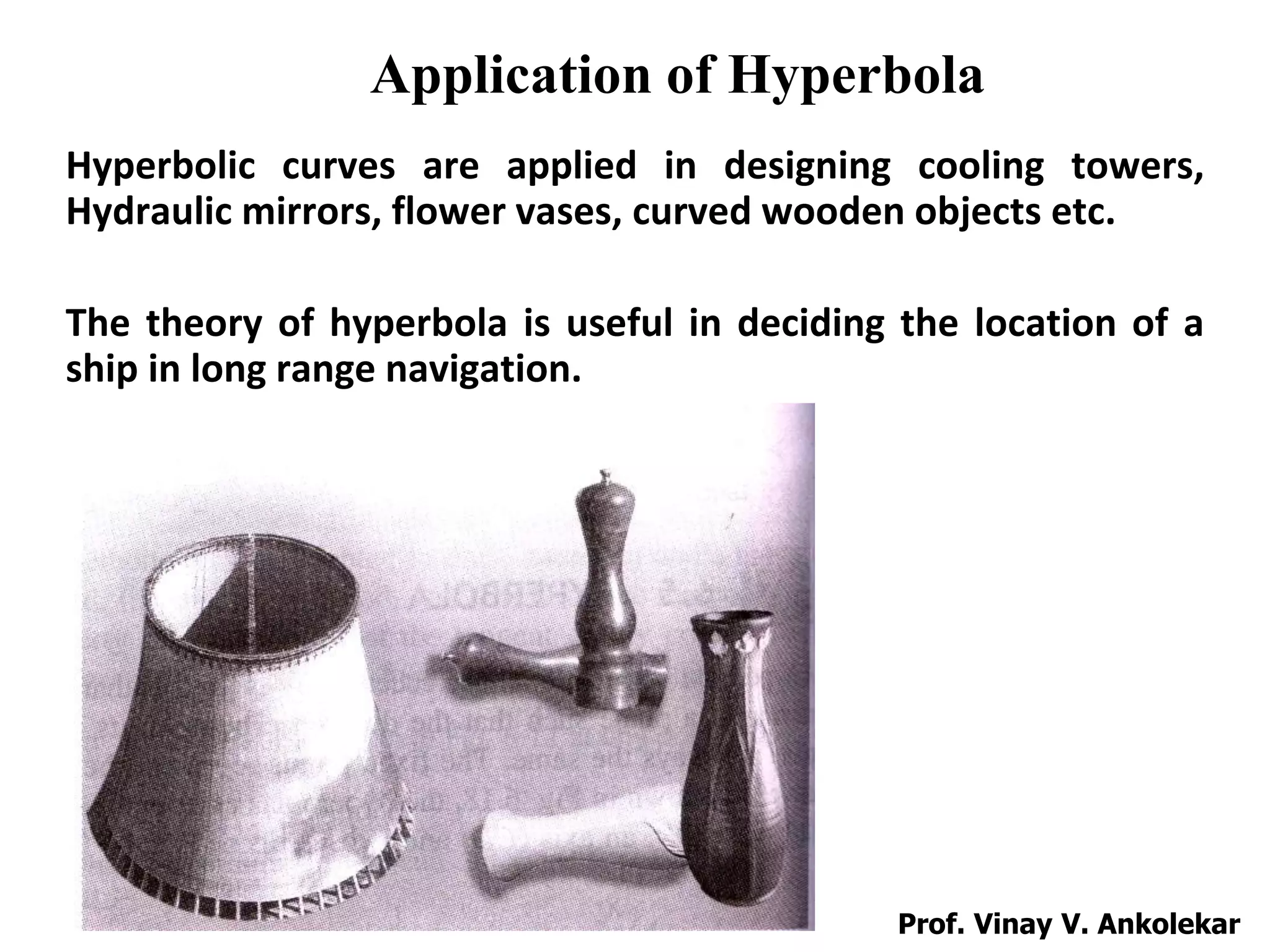
This document contains a presentation by Prof. Vinay V. Ankolekar on engineering curves and conic sections. It discusses ellipses, parabolas, hyperbolas and how they are formed by cutting a cone with different planes. Various methods for constructing these curves like directrix-focus, rectangle, and tangent methods are presented. Applications of these conic sections in areas like bridges, pipes, gears and projectile motion are also described. Several problems demonstrating the construction of these curves using different techniques are shown.

1. Presentation
By
Prof. Vinay V. Ankolekar
vinay.ankolekar@gmail.com
9404735591
Department of Mechanical Engineering
Bhivarabai Sawant College of Engineering & Research
Pune, Maharastra
ENGINEERING CURVES
Part- I {Conic Sections}

2. ENGINEERING CURVES
Part- I {Conic Sections}
ELLIPSE
1.Concentric Circle Method
2.Rectangle Method
3.Oblong Method
4.Arcs of Circle Method
5.Rhombus Method
6.Basic Locus Method
(Directrix – focus)
HYPERBOLA
1.Rectangular Hyperbola
(coordinates given)
2 Rectangular Hyperbola
(P-V diagram - Equation given)
3.Basic Locus Method
(Directrix – focus)
PARABOLA
1.Rectangle Method
2 Method of Tangents
( Triangle Method)
3.Basic Locus Method
(Directrix – focus)
Prof. Vinay V. Ankolekar

3. CONIC SECTIONS
ELLIPSE, PARABOLA AND HYPERBOLA ARE CALLED CONIC SECTIONS
BECAUSE
THESE CURVES APPEAR ON THE SURFACE OF A CONE
WHEN IT IS CUT BY SOME TYPICAL CUTTING PLANES.
Section Plane
Through Generators
Ellipse
Section Plane Parallel
to end generator.
Section Plane
Parallel to Axis.
Hyperbola
Prof. Vinay V. Ankolekar

4. Prof. Vinay V. Ankolekar

5. CIRCLE
Section plane is parallel to the base .
or
perpendicular to the axis of the cone.
Prof. Vinay V. Ankolekar

6. ELLIPSE
Section plane is inclined to the axis of cone such
that angle made by the section plane with the
axis is greater than angle made by the generator
of the cone with axis.
Prof. Vinay V. Ankolekar

7. PARABOLA
Section plane is inclined to the axis & parallel
to one of the generator of the cone.
Prof. Vinay V. Ankolekar

8. HYPERBOLA
Section plane is inclined to the axis of cone
such that angle made by the section plane
with the axis is smaller than angle made by
the generator of the cone with axis.
Prof. Vinay V. Ankolekar

9. RECTANGULAR HYPERBOLA
Section plane is parallel to the
axis of the cone and not passing
through the apex.
Prof. Vinay V. Ankolekar

10. TRIANGLE
Section plane passing through the apex of the cone.
Prof. Vinay V. Ankolekar

11. F1
C
D
D
AXIS
A
F2Ve
VpVh
Ve
DIRECTRIX
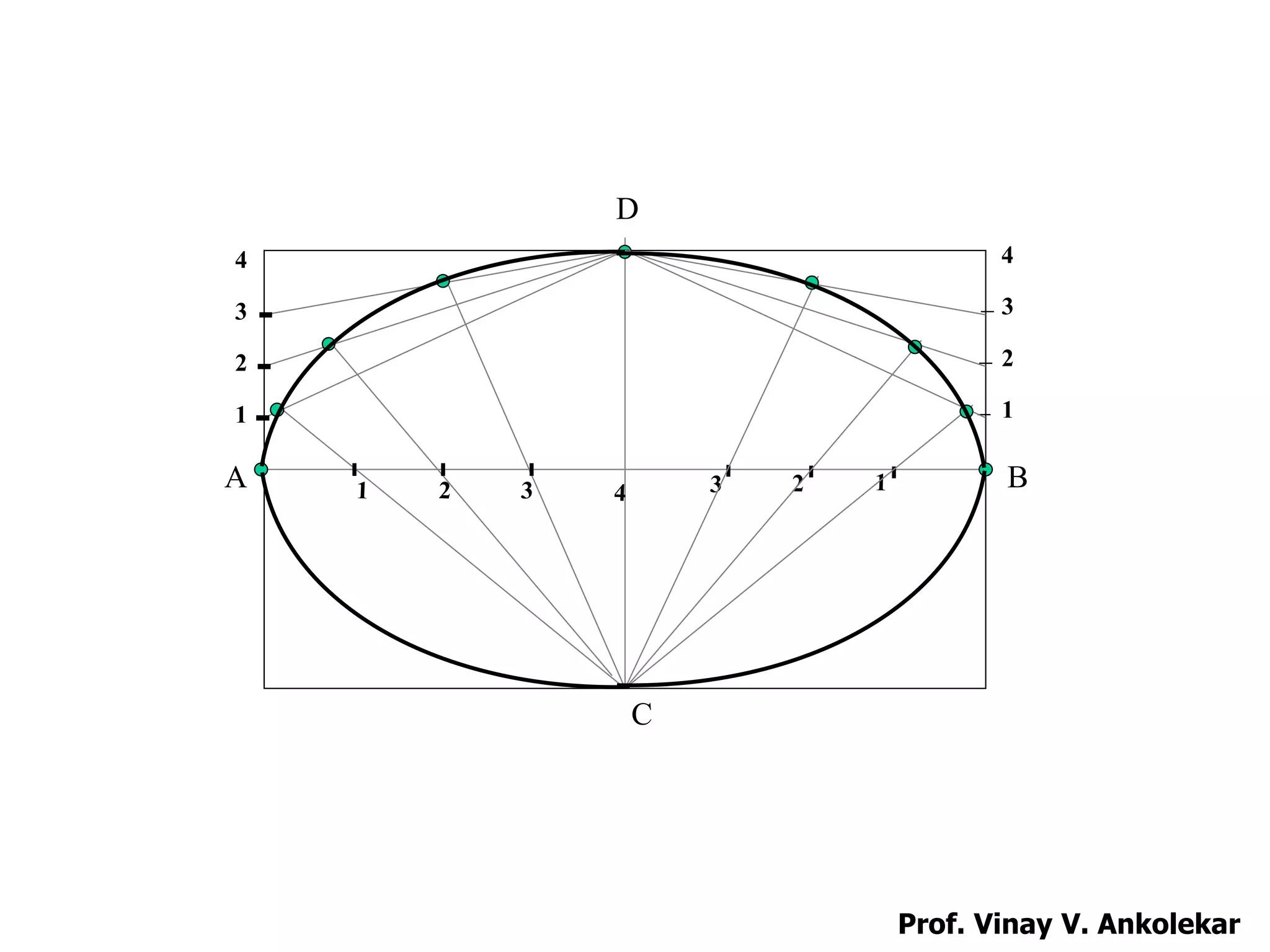
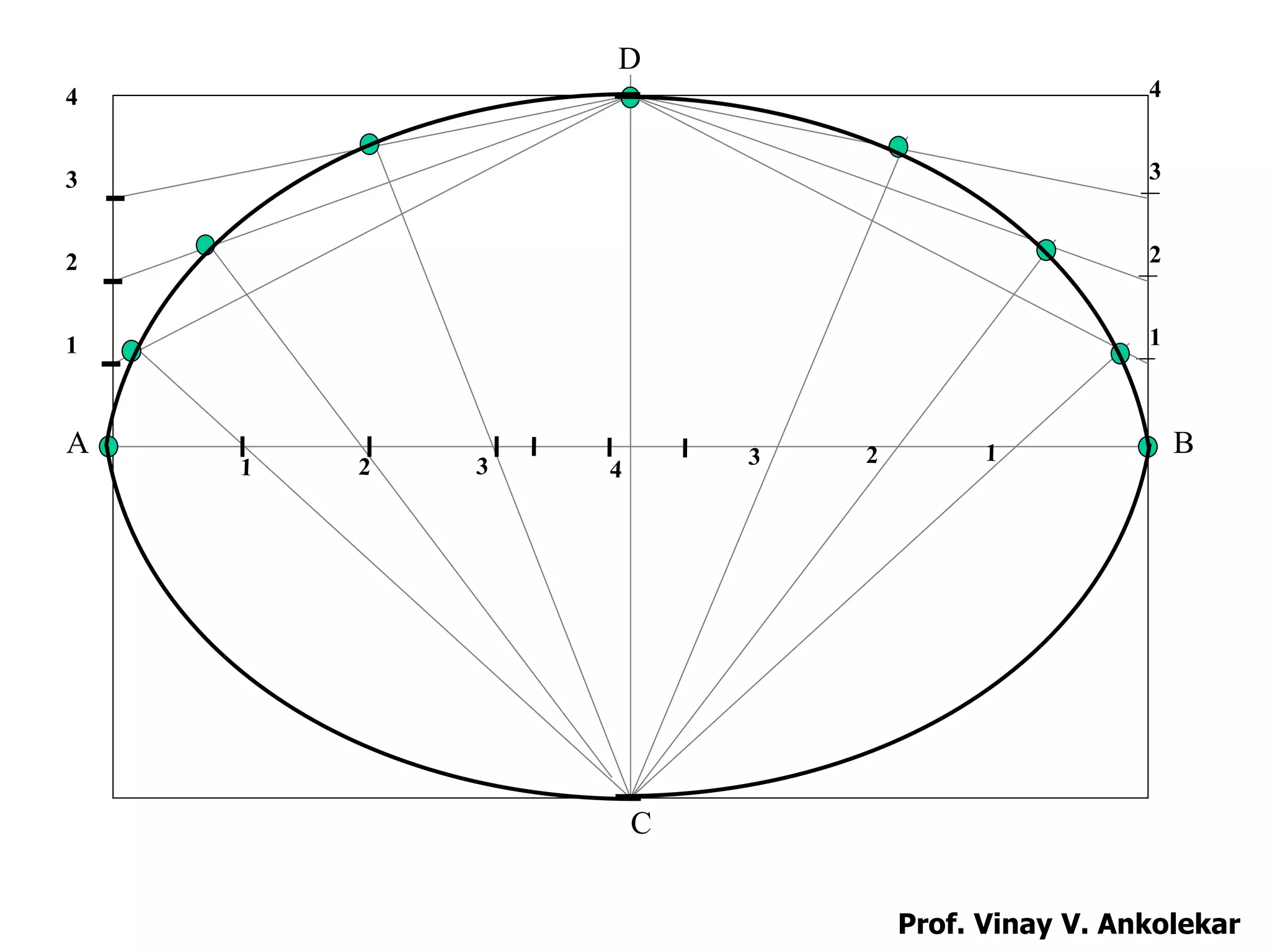
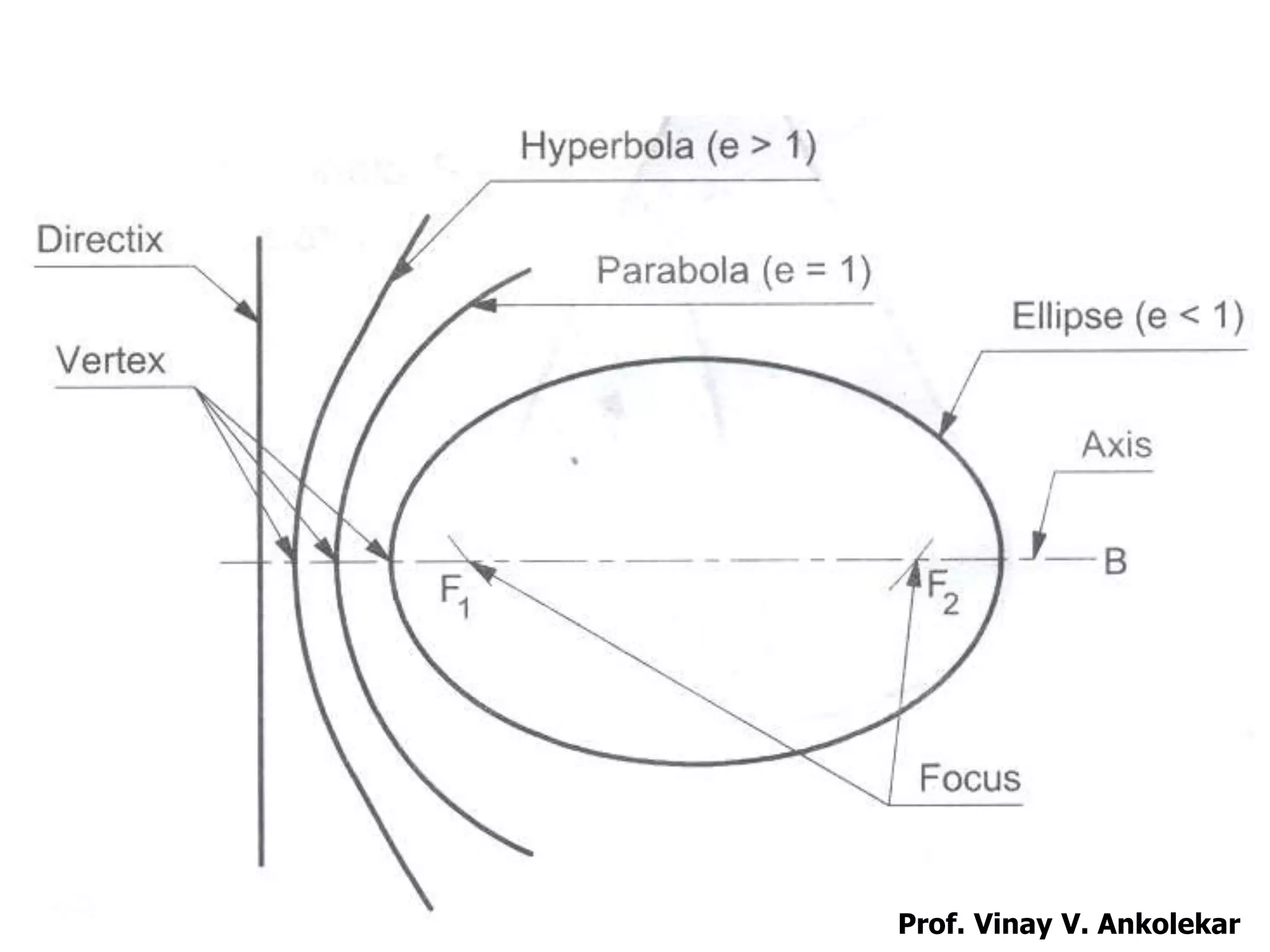
CONIC TERMINOLOGY
Focus – A fixed point [F1 AND F2]
Directrix – A fixed straight line [D-D]
Axis – A line passing through the focus and
perpendicular to the directrix [C-A]
Vertex – The point at which conics intersects the axis
[Ve Vp and Vh]
Prof. Vinay V. Ankolekar

12. Prof. Vinay V. Ankolekar

13. F1
C
D
D
AXIS
A
F2Ve
VpVh
Ve
DIRECTRIX
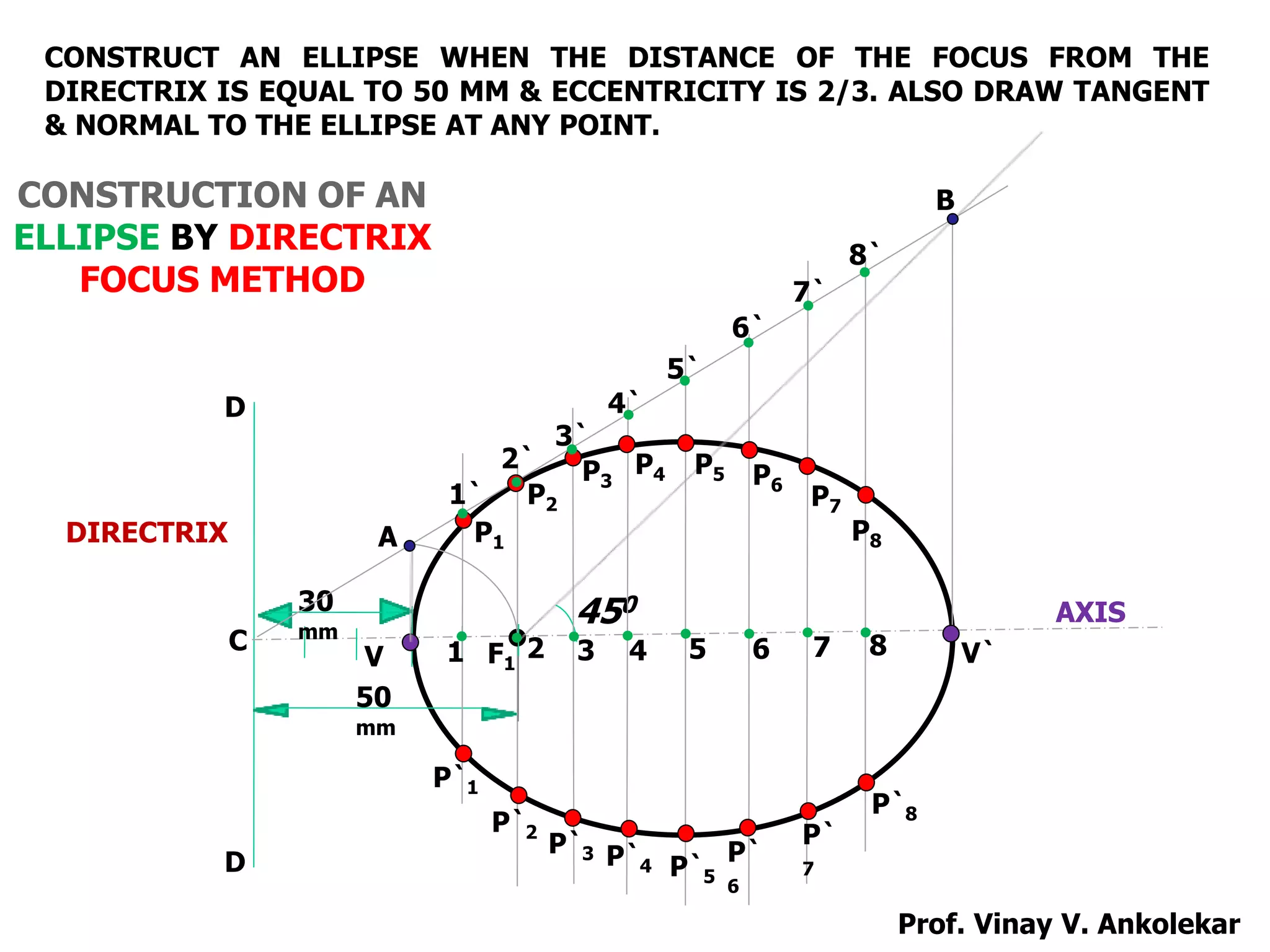
e = VF / VC
e < 1 ---- ellipse ----- [ (VF / VC) < 1 ]
e = 1 ---- parabola ----- [ (VF / VC) = 1 ]
e > 1 ---- hyperbola ---- [ (VF / VC) > 1 ]
Prof. Vinay V. Ankolekar

14. ELLIPSE
Prof. Vinay V. Ankolekar

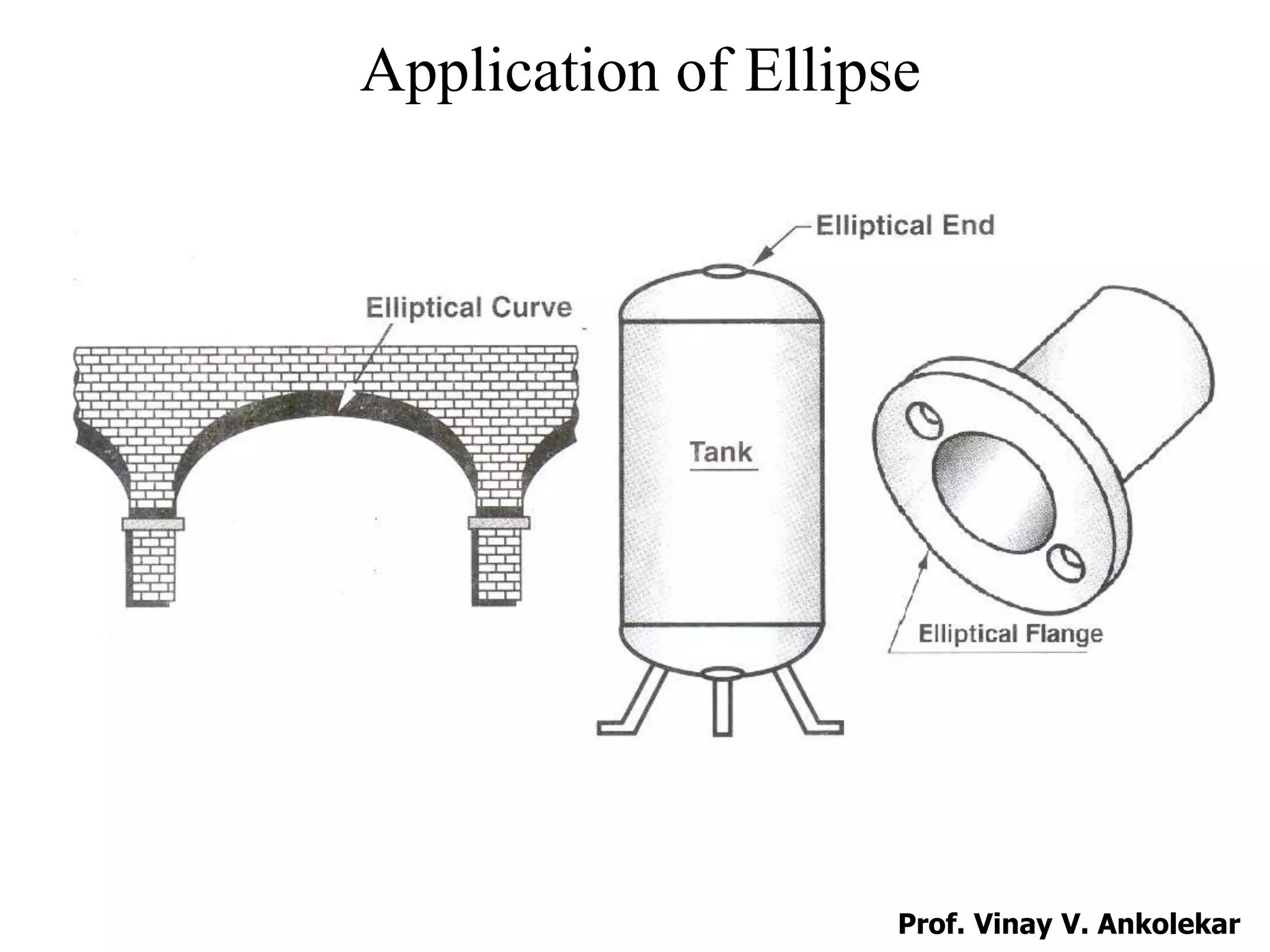
15. Applications of Ellipse
1. Arches of Bridges.
2. Pipes Bends.
3. Elliptical Gears.
4. The ends of Cylindrical Tanks are elliptical in shape.
5. Elliptical Path is followed by earth around the sun.
6. Milk Tankers.
7. Shape of Tunnels [Entry/Exit]
8. To measure the time required to cover the distance
[e.g. Missiles]
1. Designing of Kitchen Accessories [e.g. Hot Pot, Steel pots ]
2. Automobile Parts [e.g. Petrol Tanks, Head lights]
3. Shape of Eggs.
Prof. Vinay V. Ankolekar

16. Application of Ellipse
Prof. Vinay V. Ankolekar

17. Arches, Bridges, Elliptical Gears, Fancy Lamps, Bullet Nose, Stuffing Box.
Prof. Vinay V. Ankolekar

18. Application of Ellipse
Prof. Vinay V. Ankolekar

19. Application of Ellipse
Prof. Vinay V. Ankolekar

20. Prof. Vinay V. Ankolekar

21. Problem 1
Draw ellipse by Rectangle method.
Take major axis 100 mm
and
minor axis 70 mm long.
ELLIPSE
BY RECTANGLE METHOD
Prof. Vinay V. Ankolekar

22. Steps:
1 Draw a rectangle taking major and minor axes as sides.
2. In this rectangle draw both axes as perpendicular bisectors of
each other..
3. For construction, select upper left part of rectangle. Divide
vertical small side and horizontal long side into same number of
equal parts.
( here divided in four parts)
4. Name those as shown..
5. Now join all vertical points 1,2,3,4, to the upper end of minor
axis. And all horizontal points i.e.1,2,3,4 to the lower end of minor
axis.
6. Then extend C-1 line up to D-1 and mark that point. Similarly
extend C-2, C-3, C-4 lines up to D-2, D-3, & D-4 lines.
7. Mark all these points properly and join all along with ends A
and D in smooth possible curve. Do similar construction in right
side part along with lower half of the rectangle. Join all points in
smooth curve. It is required ellipse.
Prof. Vinay V. Ankolekar

23. 1
2
3
4
1
2
3
4
A B
C
D
Prof. Vinay V. Ankolekar

24. 1
2
3
4
1
2
3
4
A B
C
D
Prof. Vinay V. Ankolekar

25. ELLIPSE
DIRECTRIX-FOCUS METHOD
PROBLEM 2:-
POINT F IS 50 MM FROM A LINE AB. A POINT P IS
MOVING IN A PLANE SUCH THAT THE RATIO OF IT’S
DISTANCES FROM F AND LINE AB REMAINS CONSTANT
AND EQUALS TO 2/3 DRAW LOCUS OF POINT P.
{ ECCENTRICITY = 2/3 }
Prof. Vinay V. Ankolekar

26. 50
mm
30
mm
V F1
C
D
D
450
A
1 2 3 4 5 6 7 8
B
1`
2`
3`
4`
5`
6`
7`
8`
V`
P1
P2
P3
P4 P5 P6
P7
P8
P`8
P`
7
P`1
P`2
P`3 P`4 P`5
P`
6
CONSTRUCT AN ELLIPSE WHEN THE DISTANCE OF THE FOCUS FROM THE
DIRECTRIX IS EQUAL TO 50 MM & ECCENTRICITY IS 2/3. ALSO DRAW TANGENT
& NORMAL TO THE ELLIPSE AT ANY POINT.
CONSTRUCTION OF AN
ELLIPSE BY DIRECTRIX
FOCUS METHOD
AXIS
DIRECTRIX
Prof. Vinay V. Ankolekar

27. 50 mm
30 mm
V F1
C
D
D
450
A
1 2 3 4 5 6 7 8
B
1`
2`
3`
4`
5`
6`
7`
8`
V`
P1
P2
P3
P4 P5 P6
P7
P8
P`8
P`7
P`1
P`2
P`3 P`4 P`5
P`6
AXIS
DIRECTRIX
Prof. Vinay V. Ankolekar

28. PARABOLA
Prof. Vinay V. Ankolekar

29. Application of Parabola
The Parabolic curves are used on light
reflectors, solar concentrators, Tele-
communication dishes, Sound reflectors,
Parabolic mirrors Cantilever beams,
Missiles trajectory etc.
Prof. Vinay V. Ankolekar

30. The Projected missiles follow the parabolic path.
Prof. Vinay V. Ankolekar

31. Light reflector for
parallel beams used
in the head lamps of
the vehicle are
parabolic in shape.
LIGTH REFLECTOR
Prof. Vinay V. Ankolekar

32. The movement of objects in space under the
influence of gravity follow a parabolic path.
Prof. Vinay V. Ankolekar

33. PARABOLA
RECTANGLE METHOD
PROBLEM 3:
A BALL THROWN IN AIR ATTAINS 100 M
HEIGHT AND COVERS HORIZONTAL
DISTANCE 150 M ON GROUND.
Draw the path of the ball (projectile)
Prof. Vinay V. Ankolekar

34. STEPS:
1.Draw rectangle of above size and divide it in two equal
vertical parts
2.Consider left part for construction . Divide height and length
in equal
number of parts and name those 1,2,3,4,5& 6
3.Join vertical 1,2,3,4,5 & 6 to the top center of rectangle
4.Similarly draw upward vertical lines from horizontal1,2,3,4,5
And wherever these lines intersect previously drawn inclined
lines in sequence Mark those points and further join in smooth
possible curve.
5.Repeat the construction on right side
rectangle also. Join all in sequence.
This locus is Parabola.
.
Prof. Vinay V. Ankolekar

35. 1
2
3
4
5
6
1 2 3 4 5 6
1
2
3
4
5
6
5 4 3 2 1
Prof. Vinay V. Ankolekar

36. 1
2
3
4
5
6
1 2 3 4 5 6
1
2
3
4
5
6
5 4 3 2 1
Prof. Vinay V. Ankolekar

37. PARABOLA
DIRECTRIX-FOCUS METHOD
PROBLEM 9:
Point F is 50 mm from a vertical straight line AB.
Draw locus of point P, moving in a plane
such that it always remains equidistant from
point F and line AB.
Prof. Vinay V. Ankolekar

38. 50 mm
25m
m
V
F1
C
D
D
A
P1`
1
`
2
`
3
`
4
`
4321
P1
P2`
P3`
P4`
P2
P3
P4
e = 1
CV = VF =
25mm
25m
m
CONSTRUCTION OF PARABOLA BY DIRECTRIX FOCUS METHOD
Construct a parabola when the distance of the focus from the directrix is 50 mm &
draw a tangent & normal at a point on it 40 mm from F.
Prof. Vinay V. Ankolekar

39. 50 mm
25mm
V
F1
C
D
D
A
P1`
1`
2`
3`
4`
4321
P1
P2`
P3`
P4`
P2
P3
P4
e = 1
CV = VF = 25mm
25mm
Prof. Vinay V. Ankolekar

40. HYPARABOLA
Prof. Vinay V. Ankolekar

41. Application of Hyperbola
Hyperbolic curves are applied in designing cooling towers,
Hydraulic mirrors, flower vases, curved wooden objects etc.
The theory of hyperbola is useful in deciding the location of a
ship in long range navigation.
Prof. Vinay V. Ankolekar

42. HYPERBOLA
DIRECTRIX FOCUS METHOD
PROBLEM 4 :- POINT F IS 50 MM FROM A LINE AB. A
POINT P IS MOVING IN A PLANE SUCH THAT THE
RATIO OF IT’S DISTANCES FROM F AND LINE AB
REMAINS CONSTANT AND EQUALS TO 2/3 DRAW
LOCUS OF POINT P. { ECCENTRICITY = 2/3 }
Prof. Vinay V. Ankolekar

43. CONSTRUCTION OF HYPERBOLA BY DIRECTRIX FOCUS METHOD
The distance of a focus from the directrix is 45 mm. A point moves in such a way that
the eccentricity is equal to 3/2. Draw the locus of the point & name the curve.
50 mm
C
D
D
20
mm
V
F1
A
P1
1
1`
2 3
2`
3`
P1`
P4
P2
P2`
P4`
Prof. Vinay V. Ankolekar

44. THANK YOU
From:
Prof. Vinay V. Ankolekar