1) The document describes a modification of the game of Nim where players randomly select either an apple or orange from a bag before each turn. If an apple is selected, the player moves once, but if an orange is selected, the player must move twice and the bag is removed. 2) It provides background on the classic game of Nim and explains nimbers and strategies using nimber values to determine which player has the winning strategy. 3) The paper aims to analyze simple Nim games with chance and determine strategies given the probability p of selecting an apple.

1. Apples & Oranges: A Game of Nim with Chance
Brandon Lyles
B.S Mathematics St. John Fisher College
Rochester, NY 14618
Abstract
We take the impartial game of Nim and modify it in the following way. Let there
be an arbitrary number of apples and oranges in a bag. Before each turn a player selects
either an apple or an orange, with replacement. If an apple is selected (with probability p)
then the player will move once, otherwise they will move twice. When an orange is
selected (with probability q = 1-p) the bag is removed from the game and the game
continues under normal play for the game of Nim. Our goal is to look at simple Nim
games with chance and find strategy given a value of p.
The game of Nim has been thoroughly analyzed in combinatorial game theory,
leading to many ground breaking advances on this topic in the mathematics and computer
science communities. In this paper, we will modify the game in such a way where a
player is forced to move once or twice in a turn. This modification will allow us to
evaluate how the game is played for certain values of p. This paper serves to only look at
the combinatorial game of Nim and the modified version, Apples and Oranges.
Background of Nim
The game of Nim is considered an impartial combinatorial game. These types of
games are played with the following conditions:
Two players
A finite number of moves (the game will end eventually)
Players alternate turns
The game ends when a player cannot make a move, that player is the loser
The game of Nim consists of several finite piles of beans (where there is at least
one pile with at least one bean) and the goal is to take the last bean leaving your opponent
with no more possible moves. A legal move in this game would entail a player taking any
number of beans (at least one bean) from a single pile on his/her turn. In particular, a
player cannot take beans from more than one pile in a single turn. Once a player has
completed a legal move, it would then be the next player’s turn.
Strategy of Nim
When we speak about strategy or winning strategy in Nim, we will look at a
specific game configuration (i.e. 2 piles with 4 beans in each pile) and decide which
player will most likely win the game regardless of the moves their opponent makes.

2. Assigning nimber values to a pile of beans in the game of Nim will help in our strategy
analysis. In order to assign nimber values to a pile of beans we must first count the
number of beans in a single pile and then set the nimber value to this number. Nimbers
are simply positive non-zero numbers that are expressed in base two (all positive non-
zero integers have a unique representation in base two). Nimbers are annotated as *n,
where n is an element of the set of positive non-zero integers. For example:
Let 𝑛 = 3 such that ∗ 3 = (20
) + (21
) = 0112
When adding nimbers together we can either have a sum of zero or a positive non-
zero sum. We will demonstrate how to add nimbers by using column addition without
carry in base two. Suppose we wanted to add the nimbers: *12, *4 and *3.
1. First we need to represent these nimbers in base two
a. *12 = 23
+ 22
= 11002
b. *4 = 22
= 01002 = 1002
c. *3 = (20
) + (21) = 00112 = 0112 = 112
2. Now we will perform column addition to find the nim-sum:
23
22
21
20
1 1 0 0 = *12
+ 0 1 0 0 = *4
0 0 1 1 = *3
1 0 1 1 = *11
Note: 10112 = 23
+ 21
+ 20
= *8+*2+*1 = *11
If the sum of nimbers, nim-sum, is zero we know that Player 2 (Previous player to
move on a turn) will have a winning strategy, otherwise Player 1 (Next player to move)
has the winning strategy. Games where Player 1 has the winning strategy are called N
position games while games where Player 2 has the winning strategy are called P position
games. If we had a Game X where the configuration was three piles of beans with 12
beans in the first pile, 4 beans in the second pile and 3 beans in the third pile we could
use the column addition demonstrated above to find the nim-sum for Game X. Since the
nim-sum for Game X is a positive non-zero number (precisely the nim-sum is *11) we
know that this an N-position game.
Bouton’s Theorem [1]:
(1) From every N-position game in Nim, there is at least one move to a P-position
game.

3. (2) From every P-position game in Nim, every move is to an N-position game.
(3) All terminal moves (moves that end the game) are to a P-position game (trivial)
Proof of Bouton’s Theorem:
(1) For a game to be considered an N-position game, its nim-sum must be a positive
non-zero integer. We can turn the sum of these nimbers into zero by simply
adding the nimbers through column addition. We can do this by finding a
column with an odd number of 1’s and changing the nimbers with these 1’s in
such a way that there is an even number of 1’s in the column. Once we have
successfully done this we will have produced a P-position game.
A demonstration of the method mentioned in proof (1) is as follows:
Let’s look at Game X (stated earlier) which is an N-position game and turn it into
a P-position game through column addition without carry.
𝐂 𝟏 𝐂 𝟐 𝐂 𝟑 𝐂 𝟒
23
22
21
20
1 1 0 0 = *12
+ 0 1 0 0 = *4
0 0 1 1 = *3
1 0 1 1 = *11
As you can see there are 4 total columns in Game X where column 1 is denoted as 𝐂 𝟏 ,
column 2 is denoted as 𝐂 𝟐 , column 3 is denoted as 𝐂 𝟑 , and column 4 is denoted as 𝐂 𝟒.
Through observation we see that there are an odd number of ones in columns 1, 3 and
4.Following proof (1), we want to legally move in such a way where the number of ones
in columns 1,3 and 4 are even (we will let zero be included in the set of even numbers).
Thus, we want to take the pile with 12 beans down to a pile of 7 beans which will give us
a nim-sum of zero for Game X. This constitutes as a legal move because we took a finite
number of beans from a single pile.
𝐂 𝟏 𝐂 𝟐 𝐂 𝟑 𝐂 𝟒
23
22
21
20
0 1 1 1 = *7
+ 0 1 0 0 = *4
0 0 1 1 = *3
0 0 0 0 = *0
Hence, we have turn an N-position game into a P-position game since the nim-sum is
zero.

4. (2) Let Game Y = (∗ 𝑛1,∗ 𝑛2, … ,∗ 𝑛 𝑘), this will be a P-position game. The notation
(∗ 𝑛1,∗ 𝑛2, … ,∗ 𝑛 𝑘) is simply a game of Nim with a finite number of piles where
𝑛 𝑘 is the kth pile with a nim-value of ∗ 𝑛 𝑘. Since Game Y is a P-position game
we know that ∗ 𝑛1 +∗ 𝑛2 + ⋯ +∗ 𝑛 𝑘 = 0 which indicates that Game Y has a
nim-sum of zero. If we made such a move where ∗ 𝑛1 was changed to ∗
𝑛1
′
and ∗ 𝑛1
′
<∗ 𝑛1 then we would know that ∗ 𝑛1 +∗ 𝑛2 + ⋯ +∗ 𝑛 𝑘 = 0 = ∗
𝑛′1 +∗ 𝑛2 + ⋯ +∗ 𝑛 𝑘 is not true. If ∗ 𝑛1 +∗ 𝑛2 + ⋯ +∗ 𝑛 𝑘 = 0 = ∗ 𝑛′1 +∗ 𝑛2 +
⋯ +∗ 𝑛 𝑘 was true then ∗ 𝑛1 = ∗ 𝑛1
′
which is not true since we stated that ∗ 𝑛1
′
<
∗ 𝑛1. Therefore it is implied that ∗ 𝑛′
1 +∗ 𝑛2 + ⋯ +∗ 𝑛 𝑘 ≠ 0. Hence, we must
always turn a P-position game into an N-position game.
Now we will look at 9 different games (Games A-I) of Nim and use the concept of
nimbers to analyze which player has the winning strategy.
Game A
(Two total piles of beans: One pile of two beans and a pile with one bean)
The pile with two beans has a nimber value of *2 which is equivalent to 21
. The pile with
one bean has a nimber value of *1 which is equivalent to 20
.
When we add these nimber values together we get 21
+ 20
= 3, which is not a nim-sum
of zero, thus Player 1 has the winning strategy (N-position game). Player 1 will want to
turn the game into a game with nim-sum of zero. By Bouton’s Theorem, Player 1 can
accomplish this by taking one bean from the pile with two beans. We now have a nim-
sum of zero since ∗ 1 +∗ 1 = 20
+ 20
= 0 in base two. It is important to note that *n +*n
= 0 (using rules of binary addition without carry).
Game B
(Two total piles of beans: One pile of three beans and a pile with one bean)
The pile with three beans has a nimber value of *3 which is equivalent to 20
+ 21
. The
pile with one bean has a nimber value of *1 which is equivalent to 20
.
When we add these nimber values together we get
20
+ 21
+ 20
= ∗ 0 + 21
= ∗ 2,
which is not a nim-sum of zero thus Player 1 has the winning strategy in this game (N-
position game). Player 1 would use the same reasoning from the previous game which
was to turn the game into a zero sum game.

5. Game C
(Two total piles of beans: Both piles have two beans respectively)
Both piles have nimber values of *2 thus this is a zero sum game since *2+*2 = *0.
Therefore we know that Player 2 has the winning strategy in this game (P-position game).
We can see that using nimber values can help us find out which player will have
the winning strategy in a particular Nim game. We will list the nim value and positions
for the remaining games but leave the analysis for winning strategy to the reader.
Game D (Two total piles of beans: One pile with three beans and the other with two
beans) Nim value: *1 and Position: N
Game E (Three total piles of beans: The first pile has 2 beans and the other piles have
one bean in each) Nim value: *2 and Position: N
Game F (Three total piles of beans: The first pile has 3 beans and the other piles have
one bean in each) Nim value: *3 and Position: N
Game G (Four total piles of beans: The first pile has 2 beans and the other piles have one
bean in each) Nim value: *3 and Position: N
Game H (Four total piles of beans: The first pile has 3 beans and the other piles have one
bean in each) Nim value: *2 and Position: N
Game I (Three total piles of beans: The first two piles have 2 beans and the last pile has
1 bean) Nim value: *1 and Position: N
Play and Strategy for Apples & Oranges
Apples and Oranges is a game of Nim with an insertion of probability. The setup
for this game is as follows: A bag of apples and oranges is introduced at the beginning of
a game where the probability for each fruit is known by each player. An apple has the
probability value of p (the player can only make one legal move during his/her turn) and
an orange has the probability value of q (the player has to make two moves during his/her
turn). Please note that apples are replaced after each turn. Once an orange is selected
from the bag, the game is played under traditional nim rules and the bag is removed from
the game. In Apples and Oranges, the first player unable to move is the loser.
We will analyze the 9 games mentioned earlier for this variation of Nim. Note
that since p + q = 1, the sum of the probabilities must equal 1. When we look at a game
we must list all of the possible moves (these will be called options) a player can make

6. and figure out the probability of the player winning based on a particular move. This
analysis is for when a player goes once; when a player goes twice we will use the
analysis mentioned earlier for these games. Once we do this, we can figure out which
move is ideal, given p, for a player to make so they have the winning strategy.
Analysis on the games
Game A:
Ⓐ
ⒷⒸ
Above is Game A which is a two pile game. The first pile includes beans A and B
while the second pile includes bean C.
Option 1: Player 1 Takes A (Result: ⒷⒸ)
We will now find the probability of Player 1 winning the resulting game (ⒷⒸ) based on
the move in Case 1.
Player 1: p2
(probability of winning this game since Player 2 will take either bean B or
bean C leaving Player 1 with the remaining bean on his/her turn).
Option 2: Player 1 Takes A&B (Result: Ⓒ)
Player 1: q (Player 1 will only win the resulting game if Player 2 has to move twice
during his/her turn).
Analysis:
Take A or Take A&B?
(𝟏) p2
> q
p2
+ p − 1 > 0
p =
√5 − 1
2
Looking at the inequality helps us find which move (Take bean A or take beans
A&B) is better for Player 1 to make based on the value of p.
Based on the graph we can see that we will want to make following moves for Game A:

7. 𝐢𝐟 𝐩 <
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁
𝐢𝐟 𝐩 >
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀
Game B:
Ⓐ
Ⓑ
ⒸⒹ
Option 1: Take A
Player 1: p2
q + pq (if p >
√5 −1
2
)
The probability assigned to Player 1 tells us the probability of Player 1 winning
the resulting game if he/she decides to take bean A. So for the probability p2
q the
following events take place: Player 2 takes bean B, Player 1 takes bean C and Player 2 is
forced to take two beans but there is only one bean remaining therefore Player 1 wins the
game. For the probability pq the following events take place: Player 2 takes bean B and
Player 1 takes the two remaining beans (C and D), resulting in a victory for Player 1 since
Player 2 cannot make a move on his/her turn.
Player 1: p2
(if p <
√5 −1
2
)
Option 2: Take A&B
Player 1: p2
Option 3: Take A&B&C
Player 1: q
Option 4: Take D (trivial)
Player 1: 0
Analysis:
Take A or Take A&B?

8. ( 𝟏) if p >
√5 − 1
2
,
p2
q + pq > p2
−p3
− p2
+ p > 0
p =
√5 − 1
2
𝐢𝐟 𝐩 <
√5 − 1
2
, 𝐭𝐚𝐤𝐞 𝐀
𝐢𝐟 𝐩 >
√5 − 1
2
, 𝐭𝐚𝐤𝐞 𝐀&𝐁
( 𝟐) if p <
√5 − 1
2
,
p2
> p2
if 0 < p < 1, take either A or A&B
Take A or Take A&B&C?
(1) if p >
√𝟓−𝟏
𝟐
,
p2
q + pq > q
p2
q + pq − q > 0
2p − p3
− 1 > 0
p =
√5 − 1
2
𝐢𝐟 𝐩 >
√5 − 1
2
, 𝐭𝐚𝐤𝐞 𝐀
𝐢𝐟 𝐩 <
√5 − 1
2
, 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
(2) if p <
√5−1
2
,
p2
> q
p2
− q > 0
p2
+ p − 1 > 0
p =
√5 − 1
2

9. 𝐢𝐟 𝐩 <
√𝟓 −𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
𝐢𝐟 𝐩 >
√𝟓 −𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀
Take A&B or Take A&B&C?
( 𝟏) p2
> q
p2
− q > 0
p2
+ p − 1 > 0
p =
√5 − 1
2
𝐢𝐟 𝐩 <
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
𝐢𝐟 𝐩 >
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁
Our conclusion for Game B is as follows:
𝐢𝐟 𝐩 <
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
𝐢𝐟 𝐩 >
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀&𝐁
Game C:
ⒶⒷ
ⒸⒹ
Option 1: Take A or B
Player 1: p2
q + pq (if p >
√5−1
2
)
Player 1: p2
(if p <
√5−1
2
)
Option 2: Take A&C or Take B&D (trivial)
Player 1: 0 (if p >
√5−1
2
)

10. Player 1: 0 (if p <
√5−1
2
)
Analysis:
Take A/B or Take A&C/B&D?
(1)if p >
√5 −1
2
,
p2
q + pq > 0
p2
− p3
+ p − p2
> 0
p − p3
> 0
p = 0 or 1
Take A/B when 0 < p < 1
(2) if p <
√5 −1
2
,
p2
> 0
p = 0
Take A/B when 0 < p < 1
Our conclusion for Game C is as follows:
𝐢𝐟 𝟎 < 𝐩 < 𝟏 , 𝐭𝐚𝐤𝐞 𝐀 𝐨𝐫 𝐭𝐚𝐤𝐞 𝐁
Game D:
Ⓐ
ⒷⒹ
ⒸⒺ
Option 1: Take A
Player 1: p4
+ pq (if p >
√5−1
2
)
Player 1: p2
q + pq (if p <
√5−1
2
)
Option 2: Take A&B

11. Player 1: p2
q + pq (if p >
√5−1
2
)
Player 1: p2
(if p <
√5−1
2
)
Option 3: Take A&B&C (trivial)
Player 1: 0
Option 4: Take D
Player 1: p2
q + pq (if p >
√5−1
2
)
Player 1: p2
(if p <
√5−1
2
)
Option 5: Take D&E (trivial)
Player 1: 0
Analysis:
Take A or Take A&B?
(1) if p >
√5 −1
2
,
p4
+ pq > p2
q + pq
p4
+ p3
− p2
> 0
p =
√5 − 1
2
if p <
√5−1
2
, take A&B
if p >
√5−1
2
, take A
(2) if p <
√5 −1
2
,
p2
q + pq > p2
−p3
− p2
+ p > 0
𝑝 =
√5 − 1
2
𝐢𝐟 𝐩 >
√𝟓−𝟏
𝟐
, 𝐭𝐚𝐤𝐞 A&B
𝐢𝐟 𝐩 <
√𝟓−𝟏
𝟐
, take A
Take A or Take D?

12. (1) if p >
√5 −1
2
,
p4
+ pq > p2
q + pq
p4
+ p3
− p2
> 0
p =
√5 − 1
2
𝐢𝐟 𝐩 <
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐃
𝐢𝐟 𝐩 >
√𝟓 − 𝟏
𝟐
, 𝐭𝐚𝐤𝐞 𝐀
(2) if p <
√5 −1
2
,
p2
q + pq > p2
−p3
− p2
+ p > 0
p =
√5 − 1
2
𝐢𝐟 𝐩 >
√𝟓−𝟏
𝟐
, 𝐭𝐚𝐤𝐞 D
𝐢𝐟 𝐩 <
√𝟓−𝟏
𝟐
, take A
Take A&B or Take D?
(1)if p >
√5 −1
2
,
p2
q + pq > p2
q + pq
Take either
(2)if p >
√5 −1
2
,
p2
< p2
Take either
Our conclusion for Game D is as follows:
𝐢𝐟 𝟎 < 𝐩 < 𝟏, 𝐭𝐚𝐤𝐞 𝐀
For the remaining games I will just summarize the results based on my analysis for each
of the games. Recall that the results are providing Player 1 with a strategy given a value
for p.

13. Game E:
Ⓐ
ⒷⒸⒹ
Our conclusion for Game E is as follows:
𝐢𝐟 𝐩 <. 𝟕𝟓𝟒𝟖𝟖 , 𝐭𝐚𝐤𝐞 𝐀
𝐢𝐟 𝐩 > . 𝟕𝟓𝟒𝟖𝟖, 𝐭𝐚𝐤𝐞 𝐀&𝐁
Game F:
Ⓐ
Ⓑ
ⒸⒹⒺ
Our conclusion for Game F is as follows:
𝐢𝐟 𝐩 <. 𝟕𝟓𝟒𝟖𝟖, 𝐭𝐚𝐤𝐞 𝐀&𝐁
𝐢𝐟 𝐩 > . 𝟕𝟓𝟒𝟖𝟖, 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
Game G:
Ⓐ
ⒷⒸⒹⒺ
Our conclusion for Game G is as follows:
𝐢𝐟 𝐩 <. 𝟖𝟏𝟗𝟏𝟕 , 𝐭𝐚𝐤𝐞 𝐀&𝐁
𝐢𝐟 𝐩 >. 𝟖𝟏𝟗𝟏𝟕, 𝐭𝐚𝐤𝐞 𝐀

14. Game H:
Ⓐ
Ⓑ
ⒸⒹⒺⒻ
Our conclusion for Game H is as follows:
𝐢𝐟 𝐩 <. 𝟖𝟏𝟗𝟏𝟕 , 𝐭𝐚𝐤𝐞 𝐀&𝐁&𝐂
𝐢𝐟 𝐩 >. 𝟖𝟏𝟗𝟏𝟕, 𝐭𝐚𝐤𝐞 𝐀&𝐁
Game I:
ⒶⒸ
ⒷⒹⒺ
Our conclusion for Game I is as follows:
𝐢𝐟 𝟎 < 𝐩 < 𝟏, 𝐭𝐚𝐤𝐞 𝐄
Comments on Analysis
The analysis on the nine games above rendered some interesting results such as
the closer the value of p was to 1, the more we will implement strategies of traditional
nim (such as the nim-sum method above). Also, we notice that the critical values for p
were growing closer to 1 as the number of piles increased.
Theorem:
For any random nim game Ω, ∃ p’ < 1 such that if p > p’ then the strategy for play in
Game Ω is the same as that in traditional Nim.
Proof:

15. Let n be the number of beans in Game Ω, we know that there can be at most n moves
made in Game Ω. Therefore n is an upper bound on the number of moves made in the
Game Ω. The probability 𝑝 𝑛
is the probability that no one will move twice in the Game Ω
while 1-𝑝 𝑛
is the probability that someone will move twice in Game Ω. Set p’ equivalent
to 1-𝑝 𝑛
since they are both less than 1. Furthermore, when 𝑝 𝑛
> 1-𝑝 𝑛
we will play Game
Ω the same way we would play a traditional game of Nim (based on hypothesis). Hence,
when 𝑝 > √(
1
2
)
𝑛
we will want to play any Game Ω with the same strategies for Nim.
One example of how to use the analysis for a game of Apples & Oranges is as
followed:
Game I: There is a bag of 12 apples and 7 oranges.
ⒶⒸ Therefore p = .632
ⒷⒹⒺ
If Player 1 picks an apple from the bag, he/she will want to take bean E (hoping
that Player 2 grabs an apple on his/her turn and then Player 1 grabs an apple or an orange)
If Player 1 picks an orange from the bag, he/she will want to take beans A&B or
beans C&D and then take bean C or bean A. Since an orange was grabbed the bag of fruit
is removed from the game and the game is played under traditional nim rules. Thus,
Player 1 will win this game.
Conclusion and Further Direction
Being able to automate these games would render useful to find conjectures and
build on them to potentially form theorems supplemented with proof. Looking at this
game of nim, Apples and Oranges, allowed us to see strategy from a different
perspective. When the value of p was very big (bigger than the max of critical values for
a game) we observed that the moves aligned to normal play in traditional nim. Adding
randomness to the game of Nim give us insight on how we would want to play the game
of Nim – similar to the nim-sum approach the modified game allowed us to see who
would win specific game of Nim. Also, instead of using a bag of fruit we could use a
spinner to make the game more random. For instance, the size of the bag (and fruit) may
affect the “randomness” of the game(s). For future directions we could look into adding
random games (similar to the games we analyzed above) and also evaluating the nim-sum
values for these games. Additional questions we could ask for future direction are: Do we
ever have more than one critical value for game and does it ever occur that we want to

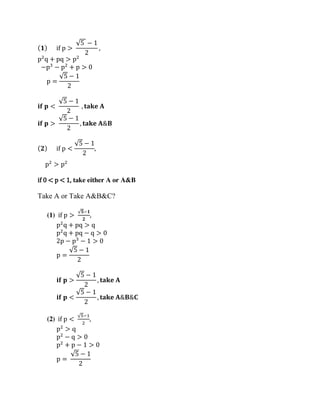
16. make the same move for distinct values of p (For example, Take A if p <.7548, take A&B
if .7548 < p < .8194, and take A if p> .8194) ?
References
[1] Theory of Impartial Games http://web.mit.edu/sp.268/www/nim.pdf
[2] Combinatorial Games http://www.ams.org/bookstore/pspdf/gsm-146-prev.pdf
[3] Thomas S Ferguson, Game Theory
https://www.math.ucla.edu/~tom/Game_Theory/comb.pdf