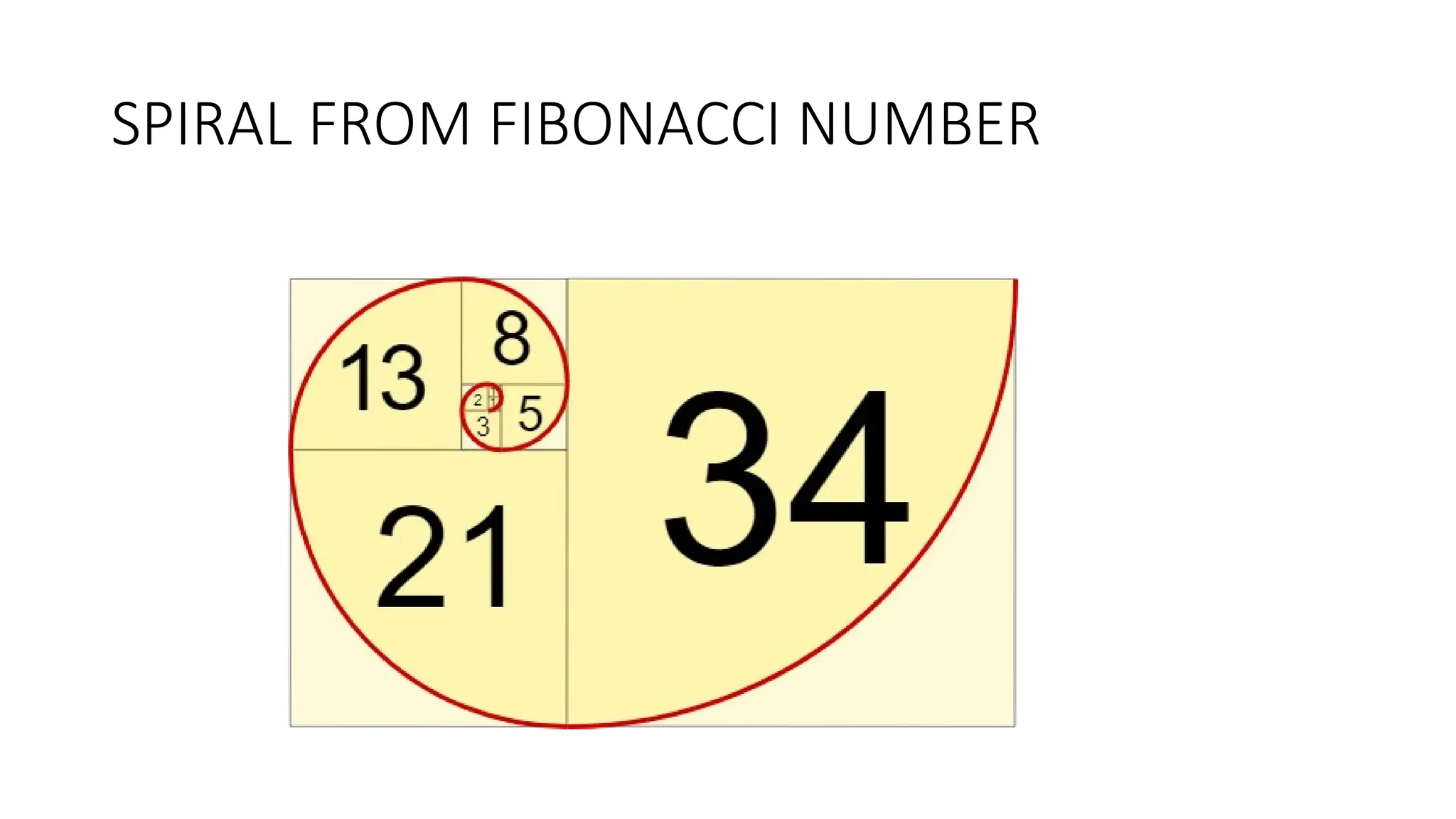
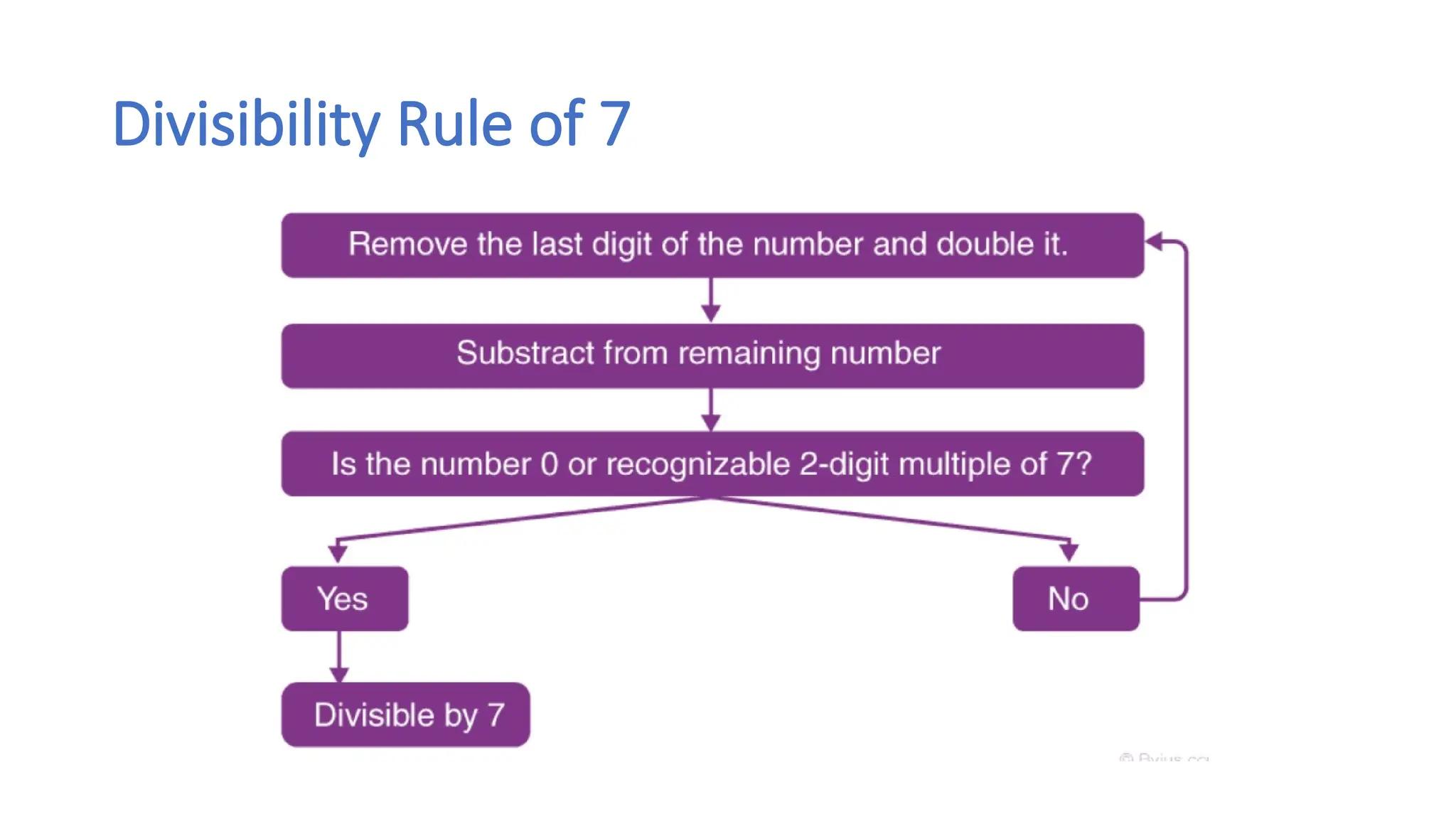
The document discusses various mathematical concepts including Fibonacci numbers, prime and composite numbers, and the Goldbach conjecture, which posits that any even integer greater than two can be expressed as the sum of two primes. It also outlines divisibility rules for numbers 2 through 13, providing tests for determining whether a number is divisible by another. These rules include checks based on factors, digit sums, and properties of the number's structure.

1. FIBONACCI NUMBER
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144,233,377,610,987, 1597, 2584,
4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418,
317811, 514229, ...

2. SPIRAL FROM FIBONACCI NUMBER

3. FIBONACCI NUMBER IN NATURE

4. PRIME NUMBERS AND
COMPOSITE NUMBERS

5. The Goldbach Conjecture
Stating that every even integer greater than two is the sum of two
prime numbers.

6. The Goldbach Conjecture
Examples

7. Divisibility Test and Magic Squares
Examples;
5 divides 30
Thus 30 = 5 X 6
divisor
Thus we write 5 30
What is the difference between 30/5 ?

8. Meaning of Divisibility
"Divisible By" means "when you divide one number by another the
result is a whole number“

9. Meaning of Divisibility

10. Why do we need to know the divisibility?
To make the division procedure easier and quicker.

11. Divisibility Rule of 2
Even numbers!

12. Divisibility Rule of 3
if the sum of its digits is divisible by 3.
Let’s test;
2343 5124 56723 127

13. Divisibility Rule of 4
If the last two digits of a number are
divisible by 4 then it is divisible by 4 completely.
Let’s check;
132 1164 1234 3456 67825

14. Divisibility Rule of 5
Which last with digits, 0 or 5
Examples;
10, 15, 220, 355, 4560, 12345

15. Divisibility Rule of 6
Numbers which are divisible by both 2 and 3 are
divisible by 6.
Meaning that we have to double-check!
1. Even numbers
and
2. the sum of its digits is divisible by 3

16. Divisibility Rule of 7

17. Divisibility Rule of 7
Let’s try
1. 546
2. 1454
3. 3724

18. Divisibility Rule of 8
If the last three digits of a number are divisible
by 8, then the number is completely divisible by
8.
Let’s check;
24344
78532

19. Divisibility Rule of 9
If the sum of digits of the number is divisible
by 9, then the number itself is divisible by 9
(same as the divisibility of 3)

20. Divisibility Rule of 10
All numbers that end with

21. Divisibility Rule of 11
If the difference of the sum of alternative digits of a number is
divisible by 11, then that number is divisible by 11 completely.
Sum of digits in odd places – Sum of digits in even places = 0 or
a multiple of 11
Let’s try..
1595, 5016, 23456

22. Divisibility Rule of 11
More rules;
If a number of digits is even, add the first digit and
subtract the last digit from the rest of the number.
Example: 3784
Number of digits = 4
Now, 78 + 3 – 4 = 77 = 7 × 11
Thus, 3784 is divisible by 11.

23. Divisibility Rule of 11
More rules;
If the number of digits of a number is odd, then
subtract the first and the last digits from the rest
of the number.
Example: 82907
Number of digits = 5
Now, 290 – 8 – 7 = 275 × 11
Thus, 82907 is divisible by 11.

24. Divisibility Rule of 12

25. Divisibility Rule of 13