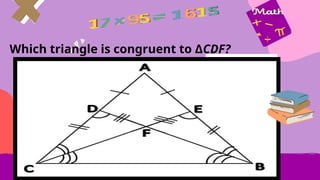
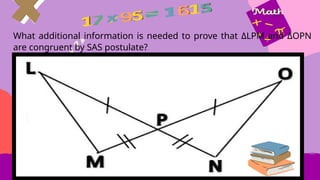
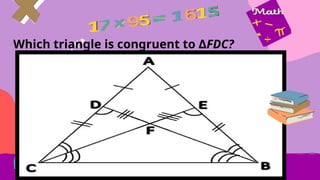
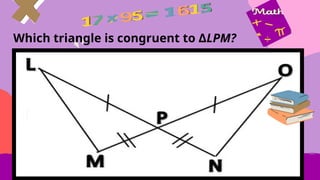
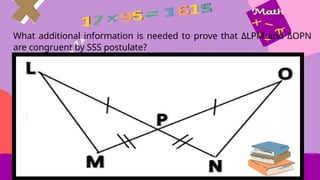
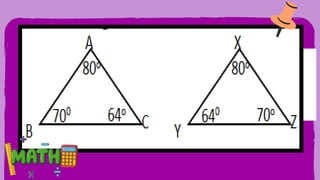
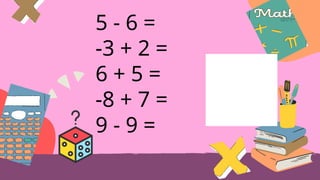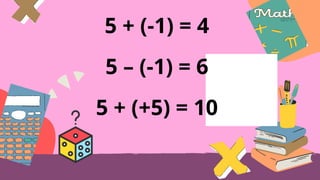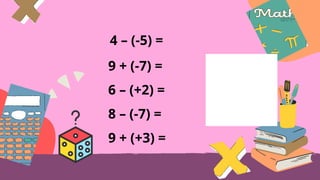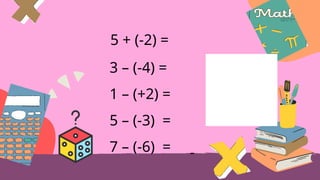This document provides an overview of integers, including their definition, operations such as addition and subtraction, and the concept of factoring polynomials. It explains how to find the greatest common factor (GCF) of integers and polynomials using prime factorization and illustrates its application with examples. Additionally, it touches on properties of triangles, congruence, and various mathematical properties related to equality.

1. INTEGERS

2. What is an Integer?

3. An integer is a positive or negative
whole number, including 0.
…-3, -2, -1, 0, 1, 2, 3…

4. There are
“4” Integer Operations

5. Addition +
Subtraction -
Multiplication x
Division ÷

6. 5 - 6 =
-3 + 2 =
6 + 5 =
-8 + 7 =
9 - 9 =

7. 5 + (-1) = 4
5 – (-1) = 6
5 + (+5) = 10

8. 4 – (-5) =
9 + (-7) =
6 – (+2) =
8 – (-7) =
9 + (+3) =

9. 5 + (-2) =
3 – (-4) =
1 – (+2) =
5 – (-3) =
7 – (-6) =

10. Factoring
Polynomials

11. The Greatest Common Factor
Factoring Trinomials of the Form x2 + bx +
c
Trinomials of the Form ax2 + bx +
c
Factoring Trinomials of the Form x2 + bx + c
by Grouping
Factoring Perfect Square Trinomials and Dif
ference of Two Squares
COMPETENCIES

12. The Greatest Common
Factor

13. Factors (either numbers or polynomials)
When an integer is written as a product of integers, each of
the integers in the product is a factor of the original number.
When a polynomial is written as a product of polynomials,
each of the polynomials in the product is a factor of the
original polynomial.
Factoring – writing a polynomial as a product
of polynomials.

14. Greatest common factor – largest quantity that is a factor of all the
integers or polynomials involved.
The Greatest
Common Factor
Finding the GCF of a List of Integers or Terms
1) Prime factor the numbers.
2) Identify common prime factors.
3) Take the product of all common prime factors.
• If there are no common prime factors,
GCF is 1.

15. Find the GCF of each list of numbers.
1)12 and 8
12 = 2 · 2 · 3
8 = 2 · 2 · 2
So the GCF is 2 · 2 = 4.
2)7 and 20
7 = 1 · 7
20 = 2 · 2 · 5
There are no common prime factors so the GCF is 1.

16. Find the GCF of each list of numbers.
1)6, 8 and 46
6 = 2 · 3
8 = 2 · 2 · 2
46 = 2 · 23
So the GCF is 2.
2)144, 256 and 300
144 = 2 · 2 · 2 · 3 · 3
256 = 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2
300 = 2 · 2 · 3 · 5 · 5
So the GCF is 2 · 2 = 4.

17. Find the GCF of each list of terms.
1) x3
and x7
x3
= x · x · x
x7
= x · x · x · x · x · x · x
So the GCF is x · x · x = x3
2) 6x5
and 4x3
6x5
= 2 · 3 · x · x · x
4x3
= 2 · 2 · x · x · x
So the GCF is 2 · x · x · x = 2x3

18. If no sides of a triangle are
equal, then the triangle is
classified as ______________.

19. What is the measure of the
angle which is the
complement of an angle
measures 48o
?

20. Two nonadjacent angles formed
by two intersecting lines are
called ____ angles.

21. What property is illustrated in the
statement, “If ∠A ≅ ∠B, ∠B ≅ ∠C
then ∠A ≅ ∠C”?

22. Which triangle is congruent to ΔCDF?

23. A star in the sky
represents a __________.

24. What additional information is needed to prove that ΔLPM and ΔOPN
are congruent by SAS postulate?

25. Which triangle is congruent to ΔFDC?

26. Which triangle is congruent to ΔLPM?

27. If two legs of one triangle is congruent
to the two legs of another triangle, then
the triangles are congruent by what
theorem?

28. What are the three undefined
terms in mathematical
system?

29. What additional information is needed to prove that ΔLPM and ΔOPN
are congruent by SSS postulate?

30. Using the distributive property, 4(a+b)
=________________.
a.4a + b b. b + 4a c. 4a + 4b d. 4 + a + b

31. If the hypotenuse and an acute angle of one
triangle is congruent to the hypotenuse and
an acute angle of another triangle, then the
triangles are congruent by what theorem?

32. An angles whose sum
is equal to 180 ?

33. Angle C and E are
supplementary angles, if m<C
= 78o
, find m < E.

34. The property of equality
which justifies that if MN =
MN, then MN = MN?

35. The property of equality
which justifies that if M = N,
then N = M?