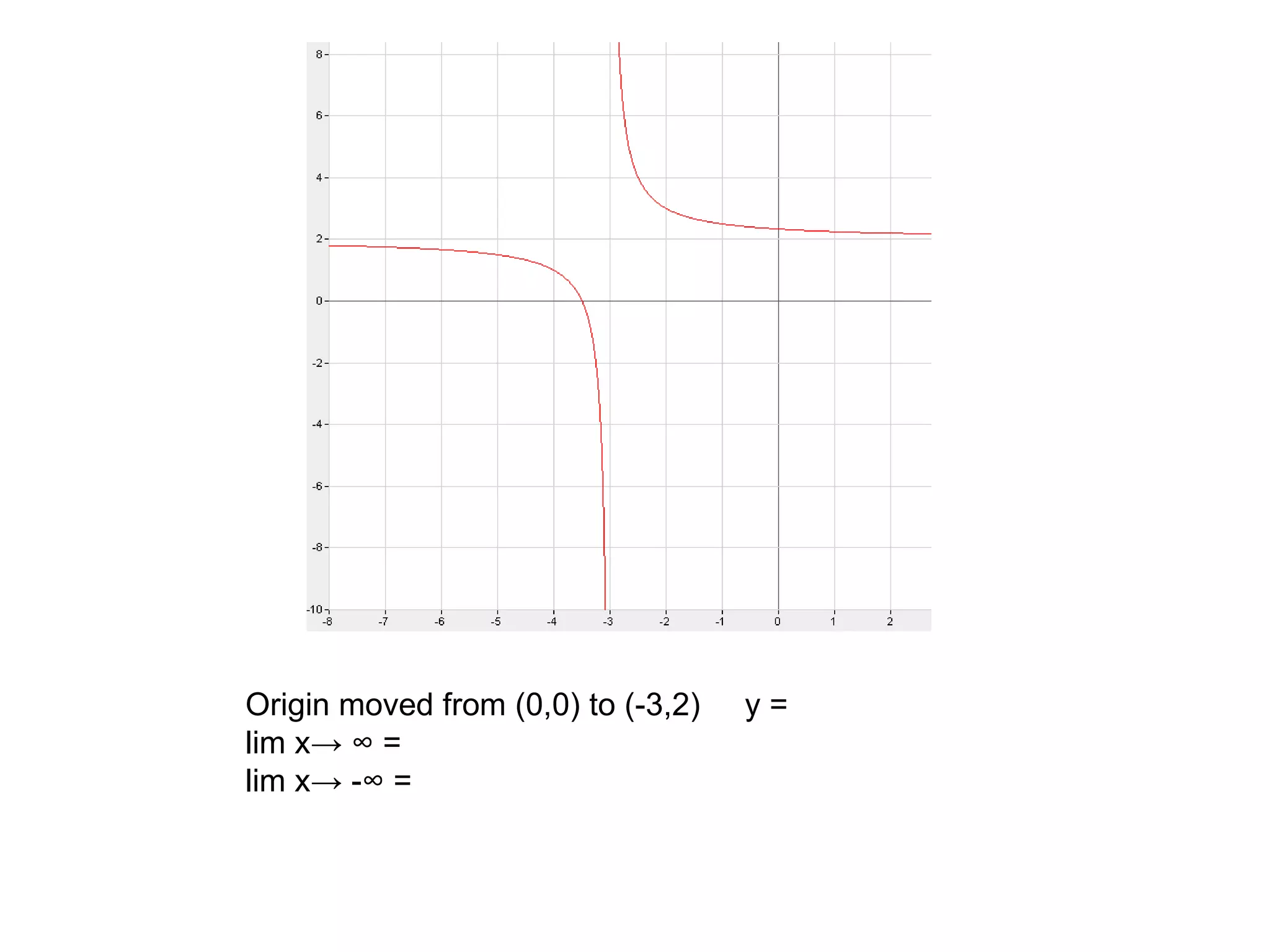
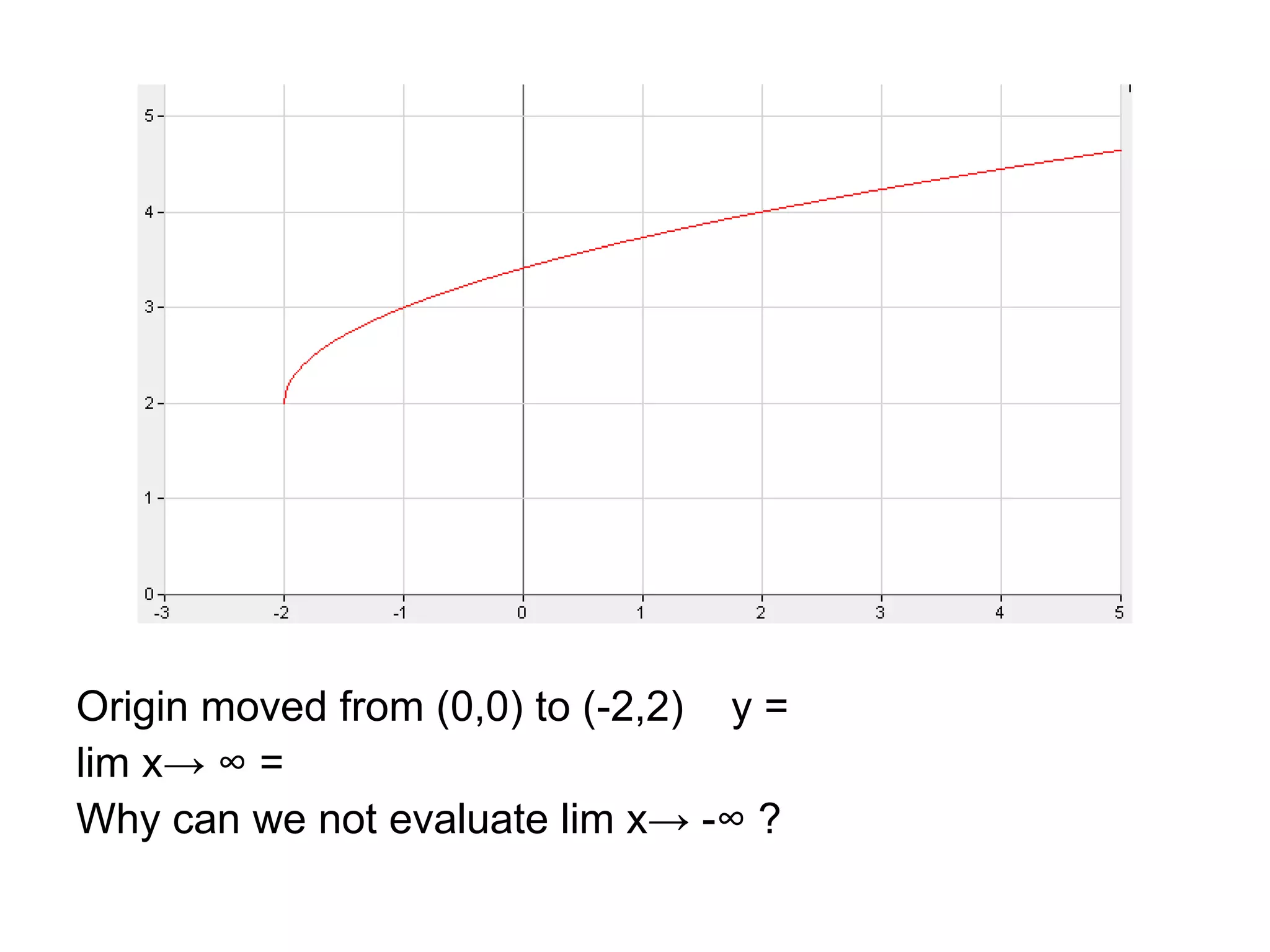
The document introduces the concept of end behavior of functions, which refers to the y-values as x takes on very large positive or negative values. This can be written using limit notation as x approaches infinity or negative infinity. For the linear function y=2x-3, the end behavior is positive infinity as x approaches positive infinity and negative infinity as x approaches negative infinity. Other functions are examined to determine their end behavior as x approaches positive or negative infinity based on transformations of the parent function y=2x.

1. End Behaviour of Functions An introduction to limits

2. What do we mean by “end behaviour”? Generally speaking, we are talking about the y-values as x takes on very large positive or negative values A convenient way to write this is with “limit notation” “ the limit as x gets close to infinity” or lim x -> ∞

3. For example Take the line y = 2x – 3 What happens to y as x takes on extreme values; what is the end behaviour?

4. lim x -> ∞ = lim x -> - ∞ = What about other functions we have reviewed so far? What can we say about their end behaviour? What are the limits as x -> ∞ and as x -> - ∞ ?

5. Origin moved from (0,0) to (4,-3) y = lim x-> ∞ = lim x-> -∞ =

6. Origin moved from (0,0) to (-3,2) y = lim x-> ∞ = lim x-> -∞ =

7. Origin moved from (0,0) to (-2,2) y = lim x-> ∞ = Why can we not evaluate lim x-> -∞ ?

8. This is a transformation of y = 2 x , 3 units left and 2 units down Y = lim x-> ∞ = lim x-> -∞ =