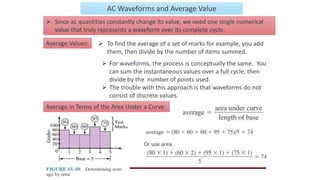
The document covers fundamental concepts in electrical technology, including electromotive force (emf), potential, current, and the differences between direct current (DC) and alternating current (AC). It discusses essential AC concepts such as cycles, frequency, phasors, and power calculations, emphasizing the distinction between active, reactive, and apparent power. Additionally, it details earthing methods and the use of megger for insulation testing, highlighting their construction and functioning.

1. ELECTRICAL TECHNOLOGY

2. Fundamentals of Electrical
• Emf – Force which moves the electrons, provided by a battery
• Potential – Amt. of energy used to move a 1 C charge from negative terminal of battery
to a point A. It is denoted by E. Unit is Volt
𝑬 =
𝑾
𝒒
• Potential difference – Amt. of energy used to move a 1C charge from point A to B.
Denoted by V. Unit is Volt
• Current – Amt of charge flowing in time t sec. Denoted by I. Unit is Ampere
𝑰 =
𝒒
𝒕

3. DC and AC
• DC has constant direction(polarity) with time
• AC direction(polarity) alternates with time
i(t) i(t)
t t
dc current
ac current
0 0.5 1 1.5 2 2.5 3 3.5
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
ac current

4. Complex Waveform

5. Fundamentals of AC
• Cycle – One set of positive and negative values of an alternating quantity
• Time Period (T)– Time taken by one cycle. Unit is sec
• Frequency (f) – No. of cycles per second
Unit is Hertz (Hz)
• Angular Frequency (ꙍ) - ꙍ= 𝟐𝝅𝒇 unit is rad/sec
• Amplitude/ peak value (Vm) – Maximum
value of positive or negative half cycle
• Peak – to - peak value – Ep-p = 2Vm
• Instantaneous Value –
𝑽 = 𝑽𝒎sinꙍt = Vmsin2πft = Vmsin
𝟐π
𝑻
t
• Phase – Horizontal distance from zero position of wave

6. Phasor Difference
 Phase difference refers to the angular displacement between different
waveforms of the same frequency.
 The terms lead and lag can be understood in terms of phasors. If you observe
phasors rotating as in Figure, the one that you see passing first is leading and
the other is lagging.

7. Voltages and Currents with Phase Shifts
 If a sine wave does not pass through zero at t =0 s, it has a phase shift.
 Waveforms may be shifted to the left or to the right

8. Introduction to Phasors
 A phasor is a rotating line whose projection on a vertical axis can be used
to represent sinusoidally varying quantities.
 To get at the idea, consider the red line of length Vm shown in Figure :
The vertical projection of this line (indicated in dotted red) is :
v =
 By assuming that the phasor rotates at angular velocity of ω rad/s in the
counterclockwise direction

9. Introduction to Phasors

10. Shifted Sine Waves Phasor Representation

11. AC Waveforms and Average Value
 Since ac quantities constantly change its value, we need one single numerical
value that truly represents a waveform over its complete cycle.
Average Values:
 For waveforms, the process is conceptually the same. You
can sum the instantaneous values over a full cycle, then
divide by the number of points used.
 The trouble with this approach is that waveforms do not
consist of discrete values.
 To find the average of a set of marks for example, you add
them, then divide by the number of items summed.
Average in Terms of the Area Under a Curve:
Or use area

12.  To find the average value of a waveform, divide the area under the waveform by
the length of its base.
 Areas above the axis are counted as positive, while areas below the axis are
counted as negative.
 This approach is valid regardless of waveshape.
AC Waveforms and Average Value
 Average values are also called dc values, because dc meters indicate average
values rather than instantaneous values.

13. • It is that DC current which transfers the same charge across a circuit as is transferred by
that alternating current
• Average value of a symmetrical alternating quantity over a complete cycle is zero
• So average value of voltage and current are not used for power calculation
Average value of AC sinusoidal waveform
(contd.)

14. RMS or Effective Value of a sinusoidal wave
RMS (Root Mean Square) value of an ac is given by that steady (d.c.) current
which when flowing through a given circuit for a given time produces the same
heat as produced by the alternating current when flowing through the same
circuit for the same time.

15. Form Factor
• It is the ratio of rms value and average value
• For an AC sinusoidal wave,
FF =
RMS value
Average value

16. Power in an AC circuit
• In a DC circuit,
Power = VI = I2R = V2/R
• But in an AC circuit,
2 2
L
P
P
Q
Q
j
S
S 
 
 
 
S
S

17. AC Real (Active) Power (P)
• The Active power (P) is the power that is dissipated in the
resistance of the load. It is the useful power that drives the load
• It uses the same formula used for DC (V & I are the
magnitudes, not the phasors):
𝑃 = 𝐼2
𝑅 =
𝑉2
𝑅
= VI cos Φ watts, W
WARNING! #1 mistake with AC power calculations!
The Voltage in the above equation is the Voltage drop across the resistor, not
across the entire circuit!
CAUTION!
REAL value of resistance (R) is used in REAL power calculations, not
IMPEDANCE (Z)!

18. AC Imaginary (Reactive) Power (Q)
• The reactive power (Q) is the power that is exchanged (travel back and
forth) between reactive components (inductors and capacitors).
• The formulas look similar to those used by the active power, but use
reactance instead of resistances.
• Units: Volts-Amps-Reactive (VAR)
• Q is negative for a capacitor by convention and positive for inductor as
an inductive load consumes the reactive power while capacitive load
generates the reactive power.
𝑄 = 𝐼2
𝑋 =
𝑉2
𝑋
= VI sin Φ [VAR]
WARNING! #1 mistake with AC power calculations!
The Voltage in the above equation is the Voltage drop across the reactance, not
across the entire circuit!

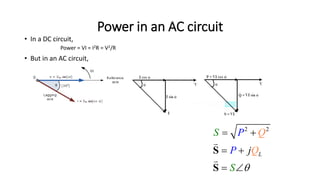
19. AC Apparent Power (S)
• The Apparent Power (S) is the power that “appears” to flow to the
load. It is the complex combination of true or active power and
reactive power
• The magnitude of apparent power can be calculated using similar
formulas to those for active or reactive power:
• Units: Volts-Amps (VA)
• V & I are the magnitudes, not the phasors.
2
2
[VA]
V
S VI I Z
Z
  

20. Power Factor

21. AC through pure Resistance only

24. AC through pure Inductance only

27. AC through pure Capacitance only

30. Series RL circuit
i = Im sin (ω t − φ) where Im = Vm / Z

32. Instantaneous Power:
Average power :

33. Series RC circuit
1. Impedance
2. Phase angle & power factor
Phasor diagram
Impedance triangle

34. Instantaneous power :
Average power :

35. Series RLC circuit
2. Impedance :
3. Phase angle & power factor :
1. Phasor diagram :
where

36. 3 cases of RLC series circuit :
Case 1 – When XL > XC
ϕ is positive
power factor is lagging
Case 2 – When XL < XC
ϕ is negative
power factor is leading
Case 3 – When XL = XC
ϕ is zero
power factor is unity
4. Impedance triangle
impedance triangle when (XL < XC)
If v = Vm sin ωt,
then i = Im sin (ω t ± φ)
+ ve sign is to be used when current leads i.e. XC > XL.
− ve sign is to be used when current lags i.e. when XL > XC.

38. Problems

41. RLC Parallel Circuit
Power = VI cosφ
+
-
+

42. Earthing
Definition : The process of transferring the immediate discharge of the electrical energy directly to the earth
by the help of the low resistance wire is known as the electrical earthing
Method: The electrical earthing is done by connecting the non-current carrying part of the equipment or
neutral of supply system to a conductor or electrode placed near or below the ground. The short circuit or
leakage current of the equipment passes to the earth which has zero potential.
Need for Earthing :
• The earthing protects the personnel from the short circuit current.
• The earthing provides the easiest path to the flow of short circuit current even after the failure of the
insulation.
• The earthing protects the apparatus and personnel from the high voltage surges and lightning discharge.

43. Earthing
Types of Earthing :
1. Wire or strip Earthing
2. Rod Earthing
3. Pipe Earthing
4. Plate Earthing

44. Pipe Earthing
• Galvanized iron (GI) and perforated pipe of approved length and diameter is placed upright in a permanently wet
soil to carry the fault current.
• The size of the pipe depends upon the current to be carried and type of soil. As per ISI, the size of the pipe is of
diameter 38 mm and 2 meters in length for ordinary soil
• The depth at which the pipe must be buried depends on the moisture of the ground. Usually, the pipe is placed at a
depth of 4.75 meters.
• The bottom of the pipe is tapered and surrounded by alternate layers of coke and salt upto a distance of 2m above
and 15 cm around the pipe to increase the effective area of the earth and to decrease the earth resistance
respectively.
• At the top, a cement concrete work is done fro protection. A funnel with wire mesh is provided in the concrete to
pour water. Perforated pipe spreads water in the layers.
• During summer the moisture in the soil decreases, which causes an increase in earth resistance. So in summer to
have an effective earth, 3 or 4 buckets of water are put through the funnel connected to 19 mm diameter pipe and
minimum length 1.25 meters, which is further connected to main earthing GI pipe.
• Another GI pipe is taken from funnel to outside to connect the earth wire
• The earth wire either GI or a strip of GI wire of sufficient cross section (14SWG) to carry faulty current safely is
carried in a GI pipe of diameter 12.7 mm at a depth of about 60cm below the ground.

45. Plate Earthing
• An earthing plate either of copper of dimension 60cm×60cm×3m or of galvanized iron of
dimensions 60 cm× 60 cm×6 mm is buried into the ground with its face vertical at a
depth of not less than 3 meters from ground level.
• The earth plate is inserted into auxiliary layers of coke and salt for a minimum thickness
of 15 cm.
• The plate is connected with GI pipe of 12.7mm dia for carrying earth wire
• The earth wire (GI or copper wire) is tightly bolted to an earth plate with the help of nut
or bolt.
• Cement work is covered with iron plate and connected with a pipe and funnel for
periodic pouring of water

46. Insulation tester/Megger/Mega-ohm-meter

47. Megger
• Portable instrument used for testing the insulation resistance of a circuit of the order of
megaohms
• Construction :
• There is a hand-driven d.c. generator. The crank turns the generator armature through a clutch
mechanism which is designed to slip at a pre-determined speed. In this way, the generator speed
and voltage are kept constant and at their correct values when testing.
• The generator voltage is applied across the voltage coil A through a fixed resistance R1 and across
deflecting coil B through a current-limiting resistance R′ and the external resistance is connected
across testing terminal XY. The two coils, in fact, constitute a moving-coil voltmeter and an
ammeter combined into one instrument.
• Working Principle:
• Two coils A and B mounted rigidly at right angles to each other on a common axis and free to rotate in a
magnetic field. When currents are passed through them, the two coils are acted upon by torques which
are in opposite directions. The torque of coil A is proportional to I1 cos θ and that of B is proportional to
I2 cos (90 − θ) or I2 sin θ. The two coils come to a position of equilibrium where the two torques are
equal and opposite i.e. where I1 cos θ = I2 sin θ or tan θ = I1/I2
• By modifying the shape of pole faces and the angle between the two coils, the ratio I1/I2 is made
proportional to θ instead of tan θ in order to achieve a linear scale.

48. Megger
• If the two coils are connected across a common source of voltage, Coil A, which is connected directly across V, is
called the voltage (or control) coil. Its current I1 = V/R1. The coil B called current or deflecting coil, carries the
current I2 = V/R, where R is the external resistance to be measured. This resistance may vary from infinity (for good
insulation or open circuit) to zero (for poor insulation or a short-circuit).
• The two coils are free to rotate in the field of a permanent magnet. The deflection θ of the instrument is
proportional to I1/I2 which is equal to R/R1. If R1 is fixed, then the scale can be calibrated to read R directly.
• (i) Suppose the terminals XY are open-circuited. Now, when crank is operated, the generator voltage so produced is
applied across coil A and current I1 flows through it but no current flows through coil B. The torque so produced
rotates the moving element of the megger until the scale points to ‘infinity’, thus indicating that the resistance of
the external circuit is too large for the instrument to measure.
• (ii) When the testing terminals XY are closed through a low resistance or are short-circuited, then a large current
(limited only by R′ ) passes through the deflecting coil B. The deflecting torque produced by coil B overcomes the
small opposing torque of coil A and rotates the moving element until the needle points to ‘zero’, thus shown that
the external resistance is too small for the instrument to measure.
• A megger can measure all resistance lying between zero and infinity, essentially it is a high-resistance measuring
device. Usually, zero is the first mark and 10 kΩ is the second mark on its scale, so one can appreciate that it is
impossible to accurately measure small resistances with the help of a megger.
• The instrument is simple to operate, portable, very robust and independent of the external supplies.