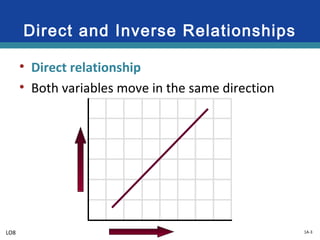
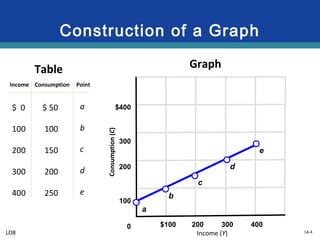
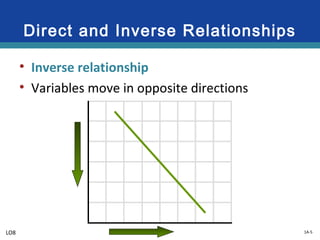
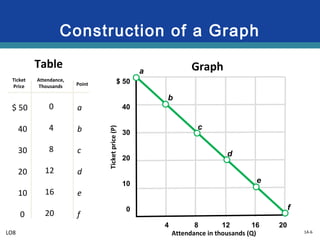
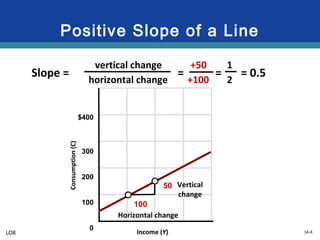
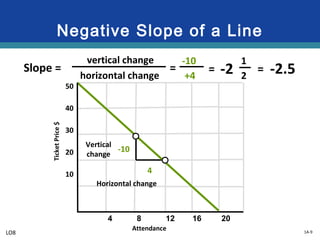
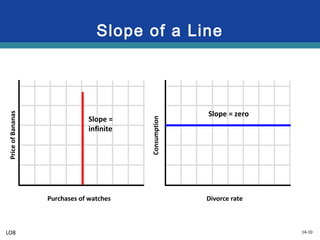
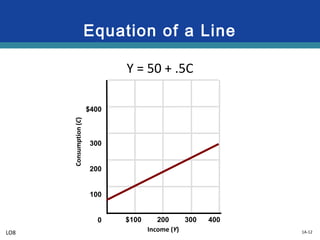
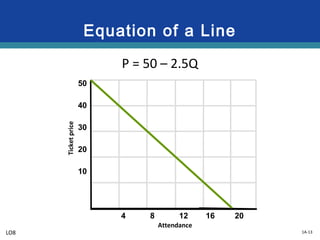
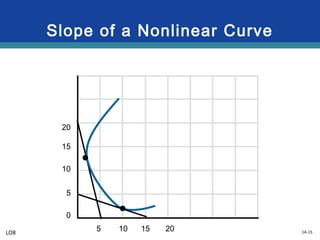
This document provides an overview of graphs and their use in representing relationships between variables. It discusses key graphing concepts such as the horizontal and vertical axes, independent and dependent variables, direct and inverse relationships, slope, and equations of linear relationships. Examples are given of direct, inverse, positive, and negative slopes in graphs of consumption-income and ticket price-attendance relationships. Nonlinear relationships are also briefly discussed.