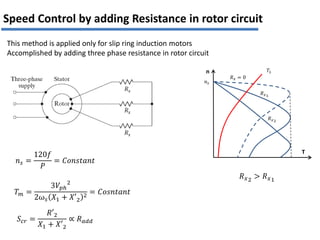
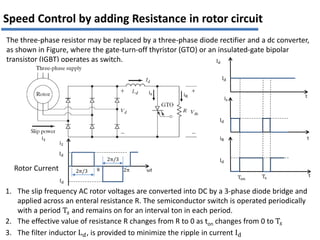
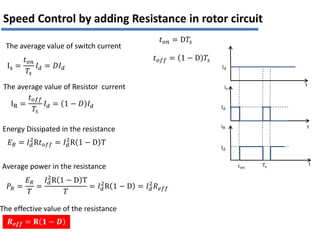
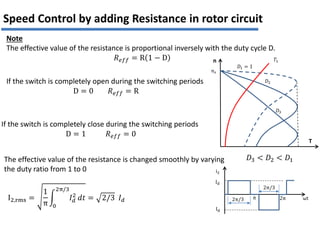
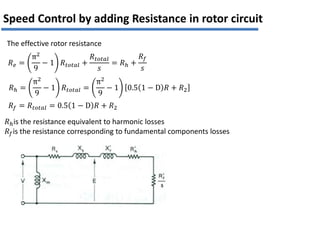
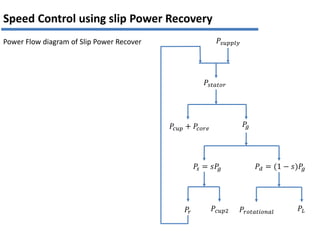
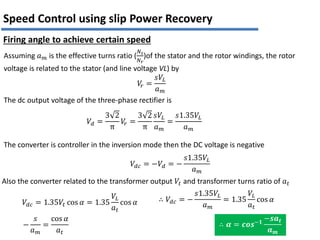
The document discusses various methods for speed control of three-phase induction motors, particularly focusing on adding resistance in the rotor circuit, which can enhance starting torque and reduce starting current. It also highlights limitations such as high power losses and the requirement for three-phase balanced resistance, alongside advanced control techniques like slip power recovery for improved efficiency and performance. Examples and calculations illustrate the application of these methods in specific motor configurations.