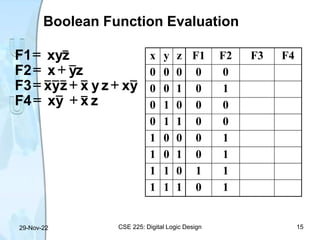
This document discusses Boolean algebra and its applications in digital logic design. It covers the basic axioms and theorems of Boolean algebra including commutative, associative, distributive, absorption, DeMorgan's theorem and duality. The principles of Boolean operator precedence and Boolean function evaluation are also explained. Examples of applying various theorems and evaluating functions are provided.

2. Overview
• Boolean Algebra
o Axioms and Theorems
o Principle of Duality
o Boolean Operator Precedence
o Boolean Function Evaluation
29-Nov-22 CSE 225: Digital Logic Design 2

3. Boolean Algebra
 A branch of mathematics that deals with
operations (AND, OR, NOT) on logical values
with binary variables.
 Based on a set of rules derived from a small
number of basic assumptions - Axioms
29-Nov-22 CSE 225: Digital Logic Design

4. Axioms
29-Nov-22 CSE 225: Digital Logic Design

5. Single Variable Theorems
29-Nov-22 CSE 225: Digital Logic Design

6. Theorems
29-Nov-22 CSE 225: Digital Logic Design
Commutative
Associative
Distributive
Absorption

7. Theorems
29-Nov-22 CSE 225: Digital Logic Design
Combining
DeMorgan’s
Theorem
Consensus

8. Proof of DeMorgan’s Theorems
29-Nov-22 CSE 225: Digital Logic Design

9. Principle of Duality
 The dual of an algebraic expression is
obtained by interchanging + and · and
interchanging 0’s and 1’s.
 The identities appear in dual pairs. When
there is only one identity on a line the identity
is self-dual, i. e., the dual expression = the
original expression.
 Unless it happens to be self-dual, the dual of
an expression does not equal the expression
itself.
29-Nov-22 9
CSE 225: Digital Logic Design

10. • F1 = (A + C) · B + 0
Dual F1 = (A · C + B) · 1 = A · C + B
• F2 = X · Y + (W + Z)
Dual F2 =
• F3 = A · B + A · C + B · C
Dual F3 =
• F4 = X · Y + Y · Z + X · Z = X · Y + X · Z
Dual F4 =
• F5 = X · (Y + Z) = X · Y + X · Z
Dual F5 =
• Are any of these functions self-dual?
Principle of Duality
29-Nov-22 10
CSE 225: Digital Logic Design

11. Boolean Operator Precedence
 The order of evaluation in a Boolean expression:
1. Parentheses
2. NOT
3. AND
4. OR
 Consequence: Parentheses appear around
OR expressions
 Example: F = A(B + C)(C + D)
29-Nov-22 11
CSE 225: Digital Logic Design

12. Problem 1
29-Nov-22 12
CSE 225: Digital Logic Design

13. Problem 2
29-Nov-22 13
CSE 225: Digital Logic Design

14. Problem 3
)
Z
X
(
X
Z
)
Y
X
( +
=
+
+ Y Y
29-Nov-22 14
CSE 225: Digital Logic Design

15. Boolean Function Evaluation
x y z F1 F2 F3 F4
0 0 0 0 0
0 0 1 0 1
0 1 0 0 0
0 1 1 0 0
1 0 0 0 1
1 0 1 0 1
1 1 0 1 1
1 1 1 0 1
z
x
y
x
F4
x
z
y
x
z
y
x
F3
x
F2
xy
F1
+
=
+
=
=
= z
yz
+
y
+
29-Nov-22 15
CSE 225: Digital Logic Design