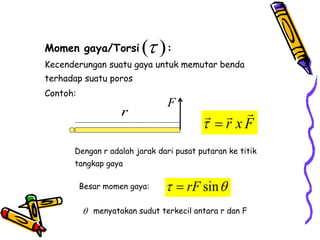
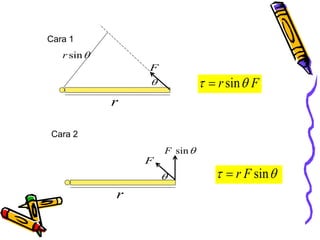
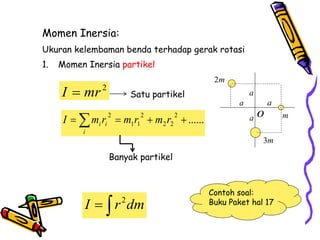
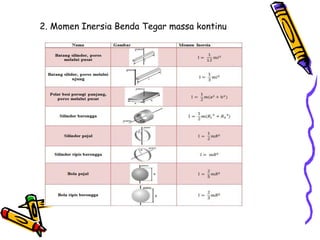
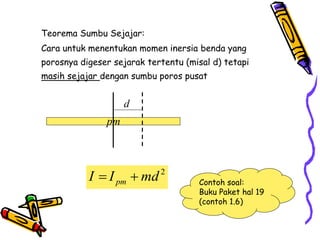
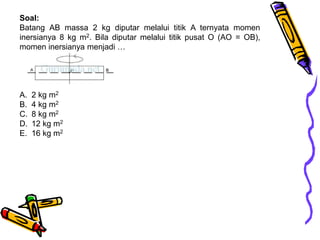
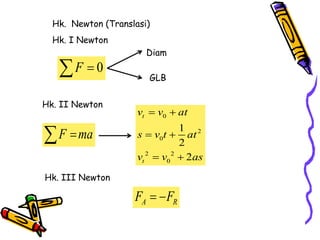
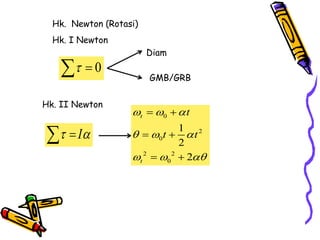
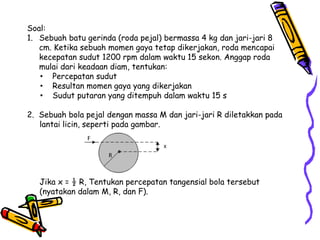
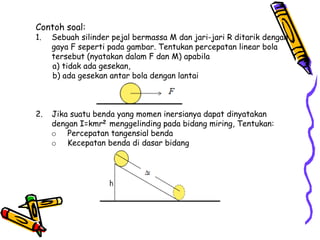
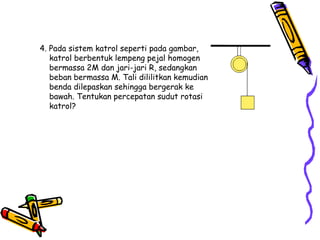
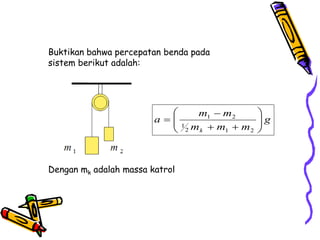
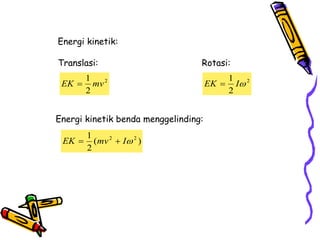
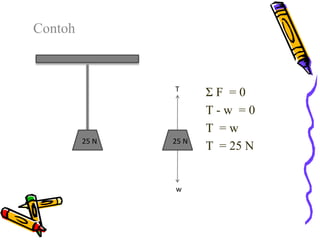
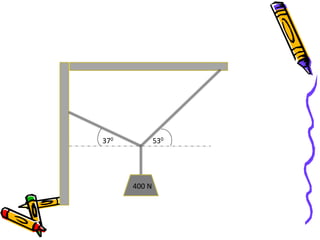
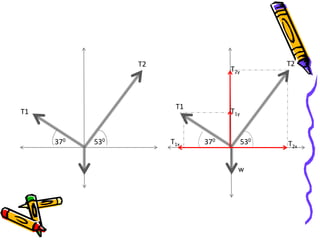
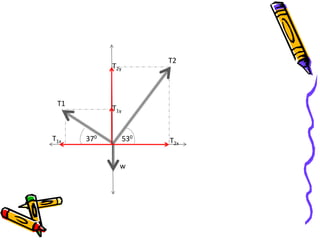
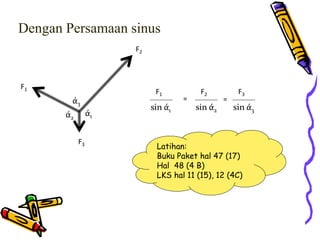
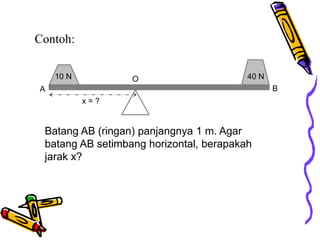
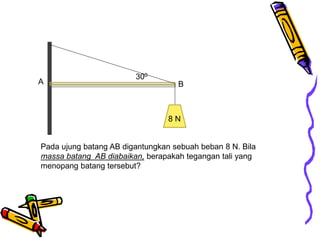
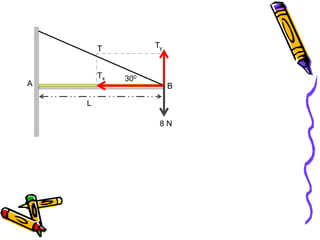
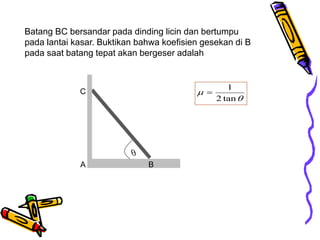
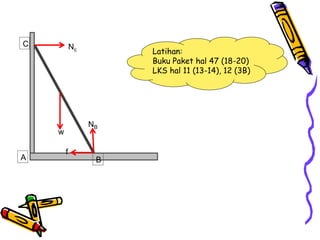
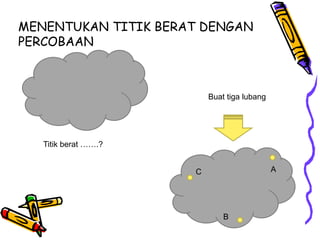
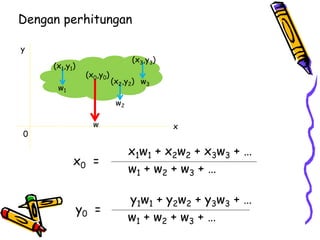
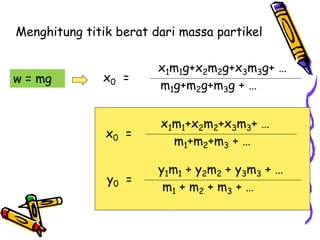
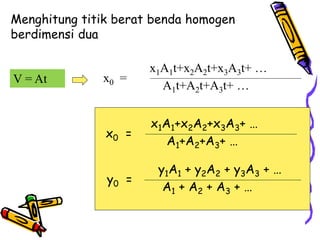
Dokumen tersebut membahas tentang dinamika rotasi dan kesetimbangan benda tegar. Secara khusus membahas konsep momen gaya, momen inersia, hukum Newton untuk gerak rotasi dan translasi, serta syarat-syarat untuk kesetimbangan partikel dan benda tegar.

1. DINAMIKA ROTASI
DAN
KESETIMBANGAN BENDA TEGAR

2. Kompetensi Dasar 3.1:
Menerapkan konsep torsi, momen inersia, titik
berat, dan momentum sudut pada benda tegar
(statis dan dinamis) dalam kehidupan sehari-hari
misalnya dalam olahraga

3. Indikator:
1. Mendefinisikan momen gaya (torsi) dan momen inersia
2. Memformulasikan momen gaya (torsi) yang bekerja pada benda
3. Memformulasikan momen inersia untuk sistem partikel dan
untuk berbagai bentuk benda tegar
4. Merumuskan hukum II newton pada gerak translasi dan gerak
rotasi
5. Menerapkan hukum II newton untuk menyelesaikan
permasalahan yang berkaitan dengan gerak benda tegar pada
berbagai kondisi
6. Menganalisis besaran-besaran fisis pada sistem benda yang
bergerak translasi dan rotasi
7. Memformulasikan hukum kekekalan momentum sudut
8. Menerapkan hukum kekekalan momentum sudut dalam
kehidupan sehari-hari
9. Menerapkan hukum newton untuk menganalisis keseimbangan
sistem partikel dan keseimbangan benda tegar.
10. Menentukan titik berat sistem partikel dan benda tegar

4. Pra Syarat
• Kinematika (GLB dan GLBB)
• Hukum Newton
• Vektor
Istilah
• Dinamika
• Rotasi
• Setimbang
• Partikel
• Benda Tegar

5. Momen gaya/Torsi :
Kecenderungan suatu gaya untuk memutar benda
terhadap suatu poros
Contoh:
)
(
F
r
r x F
 
Dengan r adalah jarak dari pusat putaran ke titik
tangkap gaya
Besar momen gaya: sin
rF
 

menyatakan sudut terkecil antara r dan F


6. F
r
 sin
r F
 

Cara 1
F
r

Cara 2

sin
F
sin
r 
sin
r F
 


7. Jarak dari poros sampai memotong tegak lurus garis
kerja gaya sering disebut lengan ( ), sehingga besar
momen gaya sering dituliskan:
lF
 
l
Tanda positif atau negatif ditentukan dari
arah putaran benda
(Konsistensi)

8. 1 2
1 1 2 2 .....
l F l F
  
 
  

Resultan Momen Gaya/Torsi
Contoh soal:
Buku Paket hal 16
Contoh 1.4
Latihan soal:
Buku Paket hal 45
No. 1, 2, 5

9. Momen Inersia:
Ukuran kelembaman benda terhadap gerak rotasi
1. Momen Inersia partikel
Satu partikel
Banyak partikel
2
mr
I 
......
2
2
2
2
1
1
2



  r
m
r
m
r
m
I
i
i
i
Contoh soal:
Buku Paket hal 17
o m
m
2
m
3
a
2
I r dm
 
a
a
a

10. Soal:
Bola A bermassa = 60 gram dan bola B = 40 gram dihubungkan
batang AB (massanya diabaikan).
Jika kedua bola diputar dengan sumbu putar di P maka momen inersia sistem adalah….
A. 12,25 .10 –4 kg m2
B. 13,50 .10 –4 kg m2
C. 14,50 .10 –4 kg m2
D. 15,50 .10 –4 kg m2
E. 16,25 .10–4 kg m2

11. 2. Momen Inersia Benda Tegar massa kontinu

12. Teorema Sumbu Sejajar:
Cara untuk menentukan momen inersia benda yang
porosnya digeser sejarak tertentu (misal d) tetapi
masih sejajar dengan sumbu poros pusat
2
pm
I I md
 
d
pm
Contoh soal:
Buku Paket hal 19
(contoh 1.6)

13. Soal:
Batang AB massa 2 kg diputar melalui titik A ternyata momen
inersianya 8 kg m2. Bila diputar melalui titik pusat O (AO = OB),
momen inersianya menjadi …
A. 2 kg m2
B. 4 kg m2
C. 8 kg m2
D. 12 kg m2
E. 16 kg m2

14. Soal:
Diberikan sebuah batang tipis dengan panjang 4
meter dan bermassa 240 gram seperti gambar
berikut:
tentukan besar momen inersia batang jika poros
digeser ke kanan sejauh 1 meter!

15. Hk. I Newton
0
F 

Diam
GLB
Hk. II Newton
F ma


0
2
0
2 2
0
1
2
2
t
t
v v at
s v t at
v v as
 
 
 
Hk. Newton (Translasi)
Hk. III Newton
A R
F F
 

16. Analogi Translasi-Rotasi



I

No Besaran Hubungan
Translasi Rotasi
1. Jarak tempuh (s) Sudut tempuh ( )
2. Kecepatan linear (v) Kecepatan sudut ( )
3. Percepatan linear (a) Percepatan sudut ( )
4. Massa (m) Momen inersia ( )
5. Gaya (F) Momen Gaya ( )




I
s r


v r


a r


2
I mr

Fr
 

17. Hk. I Newton
0
 

Diam
GMB/GRB
Hk. II Newton
I
 


0
2
0
2 2
0
1
2
2
t
t
t
t t
  
  
  
 
 
 
Hk. Newton (Rotasi)

18. Contoh soal:
Sebuah batu gerinda 2 kg dengan jari-jari 10
cm diputar 120 rad/s. Motor dipadamkan dan
sebuah pahat ditekankan pada permukaan batu
gerinda dengan suatu gaya yang memiliki
komponen tangensial 2 N. Berapa lama waktu
yang diperlukan oleh gerinda sejak gaya
diberikan hingga berhenti?
Hk. II Newton untuk gerak rotasi

 I
  I lF
 

19. Soal:
1. Sebuah batu gerinda (roda pejal) bermassa 4 kg dan jari-jari 8
cm. Ketika sebuah momen gaya tetap dikerjakan, roda mencapai
kecepatan sudut 1200 rpm dalam waktu 15 sekon. Anggap roda
mulai dari keadaan diam, tentukan:
• Percepatan sudut
• Resultan momen gaya yang dikerjakan
• Sudut putaran yang ditempuh dalam waktu 15 s
2. Sebuah bola pejal dengan massa M dan jari-jari R diletakkan pada
lantai licin, seperti pada gambar.
Jika x = ½ R, Tentukan percepatan tangensial bola tersebut
(nyatakan dalam M, R, dan F).

20. Gabungan gerak Translasi – Rotasi
1. Menggelinding pada bidang Horizontal
2. Menggelinding pada bidang miring
3. Sistem benda-katrol
sistem 1 beben dan 1 katrol
sistem 2 beban dan 1 katrol
Tips:
Untuk Menganalisis ketiga gerak diatas:
1. Gambarlah diagram bebas gaya
2. Gunakan Hukum II Newton untuk gerak translasi
dan rotasi
3. Substitusikan persamaan a r



21. Contoh soal:
1. Sebuah silinder pejal bermassa M dan jari-jari R ditarik dengan
gaya F seperti pada gambar. Tentukan percepatan linear bola
tersebut (nyatakan dalam F dan M) apabila
a) tidak ada gesekan,
b) ada gesekan antar bola dengan lantai
2. Jika suatu benda yang momen inersianya dapat dinyatakan
dengan I=kmr2 menggelinding pada bidang miring, Tentukan:
o Percepatan tangensial benda
o Kecepatan benda di dasar bidang

22. 4. Pada sistem katrol seperti pada gambar,
katrol berbentuk lempeng pejal homogen
bermassa 2M dan jari-jari R, sedangkan
beban bermassa M. Tali dililitkan kemudian
benda dilepaskan sehingga bergerak ke
bawah. Tentukan percepatan sudut rotasi
katrol?

23. Buktikan bahwa percepatan benda pada
sistem berikut adalah:
Dengan mk adalah massa katrol
g
m
m
m
m
m
a
k












2
1
2
1
2
1

24. Energi kinetik:
Translasi: Rotasi:
2
2
1

I
EK 
Energi kinetik benda menggelinding:
)
(
2
1 2
2

I
mv
EK 

2
2
1
mv
EK 

25. Hukum kekekalan energi mekanik pada gerak
menggelinding
Momentum sudut
Hukum kekekalan momentum sudut:
“Jika jumlah torsi yang bekerja pada suatu benda
sama dengan nol, maka momentum sudut sistem
konstan”
T R
EM k
EP EK EK k

  

I
L 
'
'
'
'
2
2
1
1
2
2
1
1
'






I
I
I
I
atau
I
I
L
L





Untuk partikel
2
I mr
v
r



L mrv


26. Latihan:
Buku Paket
hal 45-46
(6,7,11)
Contoh:
Buku Paket
hal 23 dan 25
(1.8 dan 1.10)

27. Dua piringan memiliki inersia masing-masing I dan 2I
dipasang pada satu poros yang licin dan dapat berputar
bersama sebagai satu sistem. Piringan pertama awalnya
diputar dengan kecepatan sudut ω dan yang kedua
dengan kecepatan sudut 2ω (keduanya berputar dalam
arah yang sama) dan kemudian keduanya disatukan dan
terus berputar dengan kecepatan sudut Ω. Ω sama
dengan....

28. Sebuah piringan berbentuk silinder pejal homogen mula-
mula berputar pada porosnya dengan kecepatan sudut 9
rad/s. Bidang piringan sejajar dengan bidang horizontal.
Massa dan jari-jari piringan 0,6 kg dan 0,2 m. bila diatas
piringan diletakkan cincin (massa dan jari-jarinya sama
dengan piringan) tepat diatas pusat piringan, maka
piringan dan cincin akan bersama-sama berputar dengan
kecepatan sudut....
a. 2 rad/s
b. 3 rad/s
c. 4 rad/s
d. 5 rad/s
e. 6 rad/s

29. KESEtIMBANGAN
PARTIKEL

30. Benda yang ukurannya dapat diabaikan/ dianggap satu titik
sehingga hanya mungkin bergerak translasi tidak bergerak
rotasi
Partikel
Syarat partikel seimbang
Σ F = 0

31. Untuk satu dimensi
Σ Fx = 0
Untuk dua dimensi
Σ Fx = 0 Σ Fy = 0
Untuk tiga dimensi
Σ Fx = 0 Σ Fy = 0 Σ Fz = 0

32. Contoh
25 N 25 N
T
w
Σ F = 0
T - w = 0
T = w
T = 25 N

33. Buku Paket hal 32
Contoh 1.13 (pelajari)

34. 400 N
530
370

35. 530
370 530
370
T1
T1
T2 T2
T2y
T2x
T1x
T1y
w

36. 530
370
T1
T2
T2y
T2x
T1x
T1y
w

37. Dengan Persamaan sinus
F1
F2
F3
ά3
ά2
ά1
sin ά1
F1
=
sin ά3
F3
sin ά2
F2
=
Latihan:
Buku Paket hal 47 (17)
Hal 48 (4 B)
LKS hal 11 (15), 12 (4C)

38. KESETIMBANGAN BENDA TEGAR
Syarat benda tegar setimbang
Σ F = 0
Σ  = 0
Buku Paket hal 33-34
Contoh 1.16-1.17 (pelajari)

39. Contoh:
10 N 40 N
x = ?
A B
Batang AB (ringan) panjangnya 1 m. Agar
batang AB setimbang horizontal, berapakah
jarak x?
O

41. 8 N
300
A B
Pada ujung batang AB digantungkan sebuah beban 8 N. Bila
massa batang AB diabaikan, berapakah tegangan tali yang
menopang batang tersebut?

42. 8 N
300
B
A
T Ty
Tx
L

43. Batang BC bersandar pada dinding licin dan bertumpu
pada lantai kasar. Buktikan bahwa koefisien gesekan di B
pada saat batang tepat akan bergeser adalah
A B
C



tan
2
1


44. A B
C
NB
Nc
w
f
Latihan:
Buku Paket hal 47 (18-20)
LKS hal 11 (13-14), 12 (3B)

46. TITIK BERAT

47. MENENTUKAN TITIK BERAT DENGAN
PERCOBAAN
Titik berat …….?
Buat tiga lubang
A
C
B

51. Dengan perhitungan
x
y
(x0,y0)
(x1,y1)
(x2,y2)
(x3,y3)
w
w1
w3
w2
x1w1 + x2w2 + x3w3 + …
x0 =
w1 + w2 + w3 + …
y1w1 + y2w2 + y3w3 + …
y0 =
w1 + w2 + w3 + …
0

52. x1m1g+x2m2g+x3m3g+ …
x0 =
m1g+m2g+m3g + …
Menghitung titik berat dari massa partikel
w = mg
y1m1 + y2m2 + y3m3 + …
y0 =
m1 + m2 + m3 + …
x1m1+x2m2+x3m3+ …
x0 =
m1+m2+m3 + …

53. x1V1+x2V2+x3V3+ …
x0 =
V1+V2+V3+ …
Menghitung titik berat benda homogen
berdimensi tiga
m = V
y1V1 + y2V2 + y3V3 + …
y0 =
V1 + V2 + V3 + …
x1V1+x2V2+x3V3+ …
x0 =
V1+V2+V3+ …

54. x1A1t+x2A2t+x3A3t+ …
x0 =
A1t+A2t+A3t+ …
Menghitung titik berat benda homogen
berdimensi dua
V = At
y1A1 + y2A2 + y3A3 + …
y0 =
A1 + A2 + A3 + …
x1A1+x2A2+x3A3+ …
x0 =
A1+A2+A3+ …

55. x1pl1+x2pl2+x3pl3+ …
x0 =
pl1+pl2+pl3+ …
Menghitung titik berat benda homogen
berdimensi satu
A = p l
y1l1 + y2l2 + y3l3 + …
y0 =
l1 + l2 + l3 + …
x1l1+x2l2+x3l3+ …
x0 =
l1+l2+l3+ …