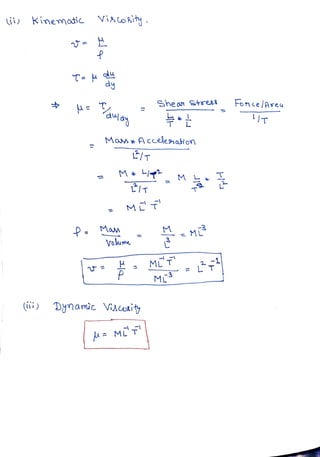
Dimensional analysis and similitude are mathematical techniques that use the study of dimensions and units to help solve engineering problems. Dimensional analysis is based on the principle of dimensional homogeneity and examines the dimensions of relevant variables affecting a phenomenon. It helps determine the systematic arrangement of variables in a physical relationship. Dimensional analysis has become important for analyzing fluid mechanics problems. It is especially useful for presenting experimental results in a concise form. Dimensional analysis ensures dimensional homogeneity. It is used to formulate equations and derive relationships between phenomena. Dimensional analysis can be used to derive equations expressed in terms of non-dimensional parameters to show the relative significance of each parameter.

1. DIMENSIONAL HNALYSIS
AND
SIMILITUDE
DIMENSioNS AND UNITS
Dimenional Anadysis v a mathemati cal technie
which makes We o the tudy o+he dimenAiona
Bolvina sevenal engineeing phoblema.
Dimenaionad analyai helba in detemining
oseangement the Vasiables in
Ayte matic
he bhyAical elationship, Combining dimenaional
Vasuables o oAm on- dimenuional paiam etess.
i baed on the piniple dimeruional
homogenij and ex the olimenionA 9helevant
Vosiables attectin he pheno menon.
Dimenionad an alysis has become an imbotant
Pluad los phoblemA. 4t
o analyain
peuially wetul in phesenHny exþesümental 1eulta
in a Concie foam.

2. Ube Dimeniona Anokyi
To e dimenuiona Homogenuty.
8 To hotiona Fomudae on a tlou
derive
Phemo menon.
3. To desive euation expheszed in tesmA o
non dimenkional ponameteu to Ahou he
nelahive gnficoance o ench panameter
Advantage o Dimenaional Analytis
4. 9 exphekse he funchonal nelaHionahip
betueen Vasuable in dimensionleta teams
a 4 enables geting athe0nehcal eguation
in a Aimplified dimenbional tom.
3. Dimensionad analyais phovide& partadAouions
to the bhoblems that ane toD Complex to be
dealt usih methe mahcally.
4 The Convenion unik uantiis from one
AyAtem anohen i fauli tated.

3. TMENSIONS.
The Voi ous phical uantities Wed in ud
phenomenon Can be exþheMedim tems
tundamental antities.
The undamental uantities ne ma, Lengh
time and tempenotne de ignot ed yete
M,T,6hupectivey
Secomdany On Deived Quantidties.
Those uanites wuch Po88esA mOne han 0ne
than
tundamental dimenuion.
e- VelsChy (LT), denaihy (ML")
e-s
he
The
he expneMions (LT), (MCS) ane Called he
dimensions veloty and denuity neAkecively
4he dumemsions 4he fowing
Detenmine
uanhiies
Ci Kinematic ViACoBity
( Dischange
V SpeRe weight
() Dymamic VilCosity
Dischange = Anea * Velehy

4. ii) Kinematic VistoRity.
T- u
au
Sheon Strui Fonce Area
IT
Mam*Accelesation
T
M M
M T
Mas M
youme
I L T
M r 3
(ii Dynamic Viaustity
= MC

5. ( Fonce >
Mas x Hccelenatiom
M* MLT
seitc Ldiaht
pedic weighr - weight on ce MLT
Volume Volume
= M
DIMENSIONAL HOMOG ENEITY
Di menuionad homogenikymean, the dumenions
each team in an euatiom on boh Aide^
ahe eual.
Thw ithe dimenaionA each tenm on both
sides an euation One the Aame he
equation known aM dimenion ally homogemeous.
Ler w Conides
Dimenaion LHS
V LT
LT
Dimenion o R:HS =
-H
AS
L.HS RH-S
The
he en i du'menuionally
homogeneow
So it Can be wed in ang AyAm oUnits.

6. METHODS OFDiMENSloNAL HNALYSIS.
4 he mumben Voables im Volved in a phyaical
Known, then he nelation amn
he
hemomenon ane
Vasuables Can be detenmined b folousing
the
Methods
Rayleig metnod
BucKingham' T-thebnem.
Buckingham' T-MeAhod.
when a
lange mumben o phyi col Varuables
One invokved Rayign's method dimensional
omalyais becomes
incheasingyaboiow and
Cumbenome. BuCkinghamA memdd an
imhovement oves Rayliga method
Buckingham designoted 4he dimenaionlew gnoup
by ne Gneek Apikal lektes T (Pi).
A i A hene tone. ofjen called Buckingam T- method.
BUCKINGHAM's T- TREOREM
hene One Voniables (debendent andindeberdent)
a
dimenionally homogen eow euation
and i tese Vaniables Contain m
undamentoa
Fundamental
m

7. dimensions (Buch as M, L, T etc) hen he Vcouables
09hanged into (n-m) dimensionleu tenms.
then the
ne
The&e dimensionleas tenms Che CalWed tenm,
Mahe matically, if ang Vasiable X,, depends on
indebendent Variables X,Xs,X, - Xn the uncional
euation may be utten as
X1 (Xa,Xs,Xu, Xn)
Eqn Can allo be iHen as
(K, a, Xa, - - Xnl =0
4t is dimensionall homogeneous equation
and Contain Vaiablea.
Osne m fundame ntal dimenuions, then
4 there
aCconding
Buckinghas
T-theohem, it Can be
wniten 4 femA
numben of T-tenm
In wtich mumben g T-tenmA eual o (n-m)
Hence en
becemes a
Each dimenionless TT - team iu foamed by Com bining
+ T ,T, T -T-m)
0
by Combining
mVaniables ou the total Variablex
one the e mainin -m) vaiasles.
one
i eoch am Contains (m+1) Varuables.

8. These m Vani ables which appem hepeatedy im
each TT- tenms ane Cone4enty Called nepeat ing
Vaiables and 0ne cheosen om among he
hat they gethe involve a
dimenaions and they them selves
Vaa ables Auch hey
he fund amenta
oo a dimension!ess parameten.
Ler Xa, X3X ae he hepeatin Vasuables
the Fundamentad dimensionm (M,L,T) 3
Then each tenm is onilen as
C
T x xx,
XX
n-m
-m
whene a,, b, C,j . b, G; ere. One he
Cotant, which ane deteamined
by Conside ring
dumenaional homojeniy. These Values ane Jubstituted
in en and Valuues T,TTa,Ta, T Tn-m
OMe 3ubshhued
ane obta ned. Theke Values ofTA
in en The #nal g enenal euahon fe he
he
in
pheno menon o then be ob tauned
by
exbnes n Gnmone he T-fenm aua tuncHom
the O+hen

10. The holce nepeaing vau ables, in mot
PLuid mechanicAphobjem may be
i,v,P ii) d, V, P V,
2 d,,
EXample. he he satom ce R experuenced by aPaotiall
3ubmenged body dependa upon the
velodty
denia Pluid P and 9navitohona accelenation
V, lengh he body, Vi»coAit he lid ,
Obtoin dimenionlem expheion o R.
Step 1. The nesixtance R, i a
function
) Velouty V i Length i) Vio
) Deniy P ( Ghavitotional acceenotion
Matmemati colly
R-(V,1,M,P, 7)
TR,V, H,P,3) =
0n
Totw mumbes
Variables,n = 6
m i obtaimed
witin2 dimeniona o
each variables
R= MLT V LT, H-MLTP M
LT
Thu the fundamental dimensiona in the phoblem
ane M, L, T
the
Cmd Hence m 3

11. Numben dimenion leas
TT-tem3= M-m= 6-3 3
Thu thnee TT-teama >ay , T2,and Ta One
fomed
The en (i) may be uOrí ten an
T, T,T) =
O
Stepa. Selection nepeating Vaiables
Out 3ix Vaiables R, V, 2,4, f,3 thonee vaiables
(as m 3) ane to be eected a
nepeatina vai ables.
R i a
debendent Variable and hould mot be
Aelected a
hepeatins Varuable.
Our Five vasiables one Vauable Ahoudd have
geometic phopenty, second Ahould have Fow propenty
and hiad Ahould have+aid propenty. hexe neuinementy
Ohe me by electina , Vand f a
epeatin variables.
The nepcating vaia bles themselves Ahould not fonm
a
dimenuionlem team and must Contain jointiy all
tundanmental dimenions eual to m i.e, 3 hene.
Dimenaions , v and P ane LLT, ML and hence
the
hhee tundamental dimenusiony exist in ,Vand
P and alo mo
the
dimension les gaoup is temmed
by hem.

12. Step3. Each T - team(=mt)Vaiobles is itten a
C
b
TT=V R
(ii)
Step 4. Each T- tenm
3olved by the phini ple
the princi ple
dimeuion al homo
geneity
TT, tem
TT R
C
P
C
MT LCLT) (M (ML T*)
Euating the exponentA M,L and T
nespetively, we ger
Fon M O = C1
Fon LL O a+b3Ci+1
T O-
b1-2
Fon
Ci-, b, -2
and a,-bt3C -1 2-3-1 = -a
Subatitung the Values a,,bi and C
in T, We gt

13. R
()
T- TeAm
b C
TT V
C
M'LT = L(LT(MC) (MËT)
Euaina M,L T 2esþechvely
Fo M: O C2t
bL O atb-31
Fo T O -b2-
C2- ba-i
a g -b+3C2t+l= -1
Subt tuhny a2 ,b, G in
T, we
aet
TT3 Team.
ba C3
MLT L (LT")(Mc3) (LT)
Euan Exponenta M, L & T espectively
ba
Fb M C3 o
Fba L: atb3 <a tl o
Fa T: 6- -b
C o, b-

14. and as- -ba+363 -1 2+0-i = 1
Substutins the Values aa, ba and 3 in
T3,
we ge
Subituk he Values o , Ta.TT in
eqni)
The func tional nelationahib become
Step 5
R
LVP
R
vP
0n
Pv
The above tephau been made on the poltulate
The
thet neurocal Pi team qnd its uane hoot
i» non-dimem>ionad.

15. FoRCES INFLUENCING HyDRAUL1C
PHENo MENA
1 TNentia Fonce (F)
away exit in the luid flos pnoblem
and hence it i Catomasy toind out the fonce
9natios oith nespect to imertia once.
i eual to poduct g mas and
accelenation he Flouwing Fuid and octs
in he dinection oppoAite to he dinection of
accelenation.
. Viscow Fonce F,)
St is phesent in Fuid flous phoblems whene
Viscosiy i o play an imþortant ole.
i euas the poduct shean stheKa[T)
due tD Viscosiy and Awnface ofheflouo.
ane a
3 navidy Fonce )
3
oben unface flous
9 pesent in , Cae
hoduc+ $ m a and accelenation due
n avit
4. P3neMne Fonce FP)
Thix to1Ce is negent in Case d
ye
pipe loo.

16. St i eual to the hoduc+ phemwme
intennty and ChOAs->ectiomal anea $the flosiny
the flousiny
intensiy
fluid
5. Sw face lension Fonce (F)
S i eual t he pnoduct Antace
sing
tenaion and ena utace he ausin
Fluid
G Eladtc FonceFe)
the poduct elantic
eual to
stress and anea the lowing fluid.
DIMENSIONLESs NUMBERS HND
THE IR SIGNIEICANCE
The dimension Less numbes» lalso Called mon-dimeniomal
The
paaamettsus) One obtained by dividing the inentia
fonce (Which auay exis when
any maw in motion)
by ViCos Tonce 0n ahaviy fonce on Þemne
tonce on face tension fonce Oh elaltic fonce.
The imbontant dimenaion leRs Mumbes ahe.
1. Reymolda Numbe Fnoude'a Numben
3. Eules'a Numbe 4. Weben' Numben
5. Mach' Num be
5.

17. Reynolds Numbex (Re)
4 i defined as the 9atio h e inestia fonce
to Viuco fonce.
Inentia
Fohce;) = Ma * Accelenation
=f* olume * Velouty
Time
P* Yokume Velochy
time
* Av*V : Volume ben Second
Anea* Velo ty AV J
fAV
Viscow FonceF) = shean Stness * cnea
T*A
du
L
PAv PVL
Reynolds No.
ReF YA
V
VL
PIP
Re
Fon
Fon pipe Flo Linea dimenion i taken
).
Vd
Re

18. The Rey nolds numbe ignifies +he elative
he
phedominance the imetia to he vi^Cow
Fonces Occwin in the los y3tem.
The Lagen the Reynold mumbe, the gheaten wi
be the elative Contibution inertia ettect.
Foude' Number (Fa)
t i denined as the 3uane noo he
natto the nentia tonce and gnavity Fonce
F;=PAv
= Mas * Accelenatiom due to ahavig
* Volume a
PAL
Fa PAv
PAL
N
F9oude's No. govemA ne dymamic Aimiloou ty
h e
fonce iA
Plo Atuatona, whene navitation al
Aigniicant and all othe
mos
ne Combcnaively negligible.
fohces

19. e Flous Ove Motches and ein
) Flos ove the 3pilluay a dam
FlowFlo hnouh Oben Channe
C) Motion Ahi in nough and tunbulent ea
Eule's Numbea (E)
defined a the Aquane noo
he imetia fonce o +he phessuwne tonce
E
F PAVv
Fp Tntensity of pnesauwe* Anea- PA
PA
Eu PIP PP
pxA
ules' s Numbes is ignificand in Plos bhoblems
in which a phe
esswne gnadient exints
DiAchange thnoug. 0ipceA, mouthbieces
(T) Pnessue ise due to udden clo8we o Valve
FLow hnough pipe
Webes Numbe ( We)
fthe nato
i de ined a
inetia fonce hee wPace tension
AJuane uo
the
foce.

20. F
We
F PAv2
F Swnface tension Fonce -Su tace tenalon *
Lengh
Pav P v
We
L
L
V
This umbe aMumea imbordtunce in flowing
Flo Aituotions
Capill any movemet watea in 3oils
i) Flos blood in veins and anteries
Mech Numbea.(M)
de fined a the uane oo he
he inentia bnce to he elasic tonce
aho
F
Fe
M
F PAV
Fe Glastc once Elasthc Streu*Anea
k*A= k*L

21. PAV2 PLy V
M=
k
k L 2
C Velociy oumd in the Pluid
M- /c.
The match umbe is im þo ntant în Comphesgi ble
flow bnob!ema at igh veloutes Such as
high velouy Flo in ipes 09 motion izh
peed ÞroJeciles and mimilea.