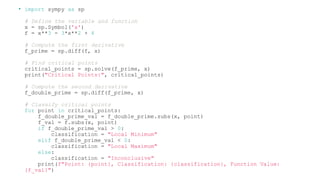
Python Methods for Numerical Differentiation For instance, let's take the function y = f (x), y = x2. Then, let's set the function value in the form of pairs x, y with a step of 0.01 for the range of x from 0 to 4. We're going to use the scipy derivative to calculate the first derivative of the function

1. Differentiation using Python

2. Determination of 1st
and 2nd
order derivative of a
function
•We use the sympy library (as sp).
•Next we define the variable and function.
• The variable as: var_name=sp.Symbol(‘var_name’)
• And function in terms of variable (Example f=
var_name**2)
•We compute the derivative as
<diff_function_name>=sp.diff(f, var_name)

3. Example:
• import sympy as sp
# Define the variable and function
x = sp.Symbol('x')
f = x**3 - 3*x**2 + 4*x + 5
# Compute the first derivative
f_prime = sp.diff(f, x)
# Compute the second derivative
f_double_prime = sp.diff(f_prime, x)
# Display the derivatives
print("First Derivative:", f_prime)
print("Second Derivative:", f_double_prime)

4. Example 2: Find the differentiation of
at
import sympy as sp
x = sp.symbols('x')
f = x**2 + 3*x + 5
f_derivative = sp.diff(f, x)
# Evaluate the derivative at x = 2
result = f_derivative.subs(x, 2)
print("Function:", f)
print("Derivative:", f_derivative)
print("Value of derivative at x=2:", result)

5. Solving a polynomial equation using sympy
from import sympy as sp
x = sp.symbols('x')
eq = x**2 - 5*x + 6 # Example: x^2 - 5x + 6 = 0
solutions = sp.solve(eq, x)
print(solutions)

6. Determining the local Minimum and Maximum of a function
• Example

7. • import sympy as sp
# Define the variable and function
x = sp.Symbol('x')
f = x**3 - 3*x**2 + 4
# Compute the first derivative
f_prime = sp.diff(f, x)
# Find critical points
critical_points = sp.solve(f_prime, x)
print("Critical Points:", critical_points)
# Compute the second derivative
f_double_prime = sp.diff(f_prime, x)
# Classify critical points
for point in critical_points:
f_double_prime_val = f_double_prime.subs(x, point)
f_val = f.subs(x, point)
if f_double_prime_val > 0:
classification = "Local Minimum"
elif f_double_prime_val < 0:
classification = "Local Maximum"
else:
classification = "Inconclusive"
print(f"Point: {point}, Classification: {classification}, Function Value:
{f_val}")