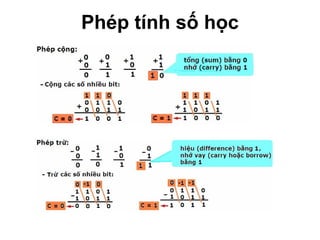
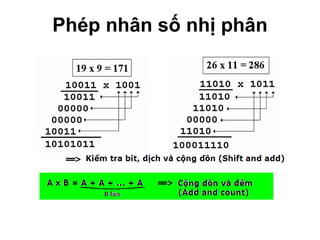
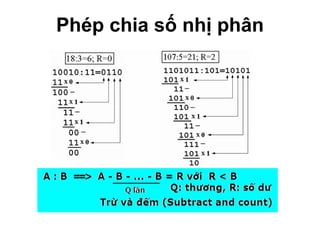
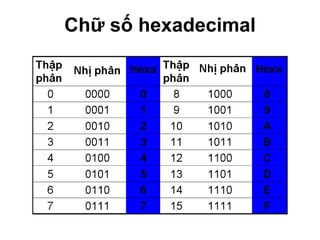
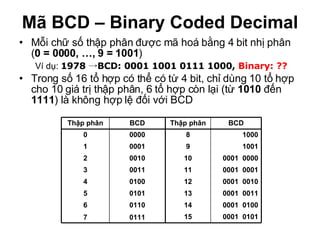
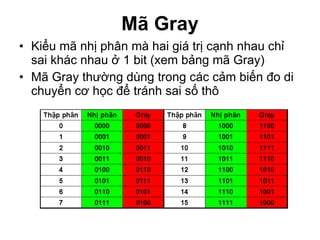
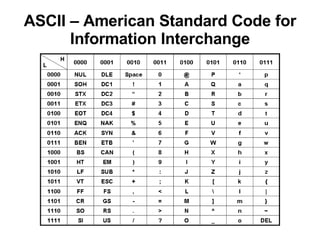
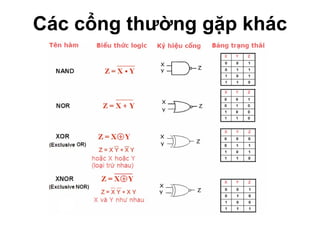
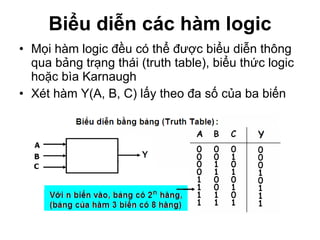
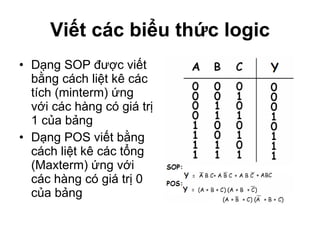
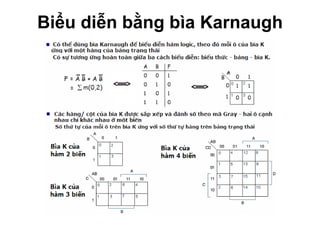
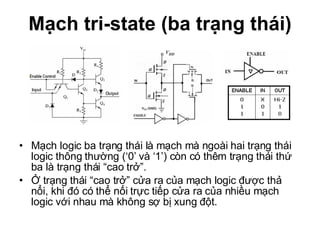
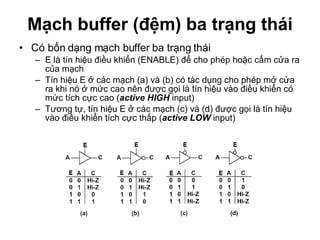
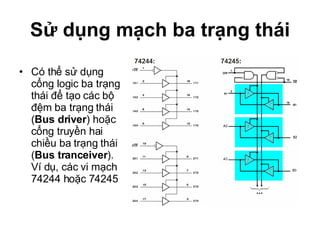
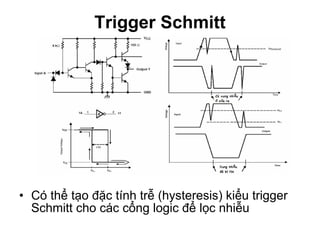
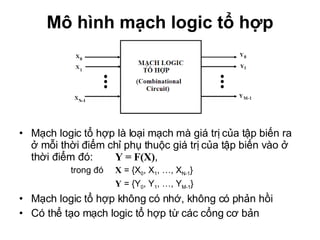
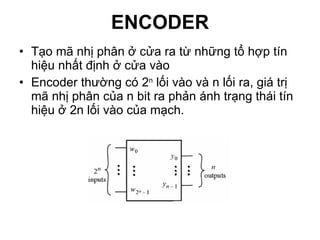
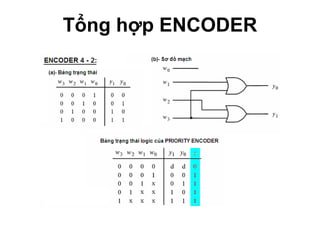
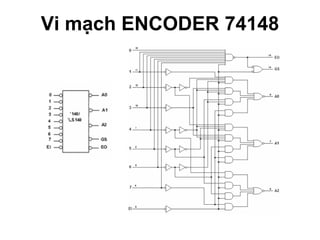
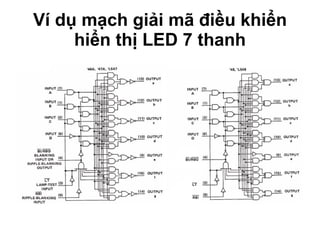
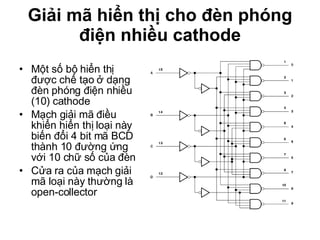
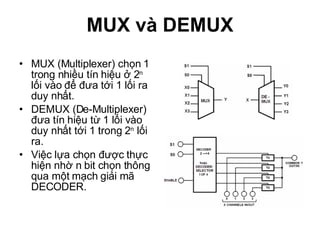
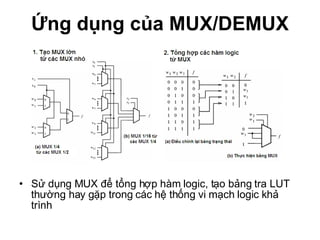
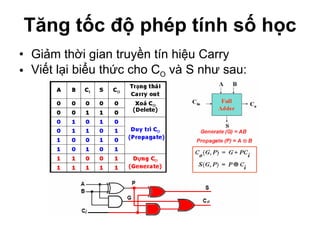
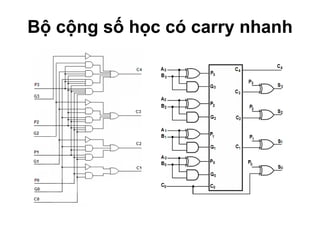
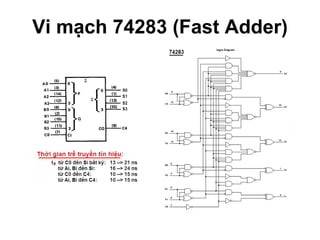
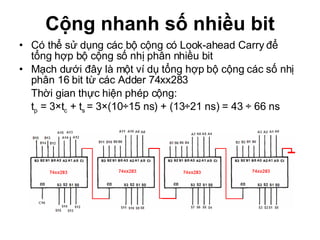
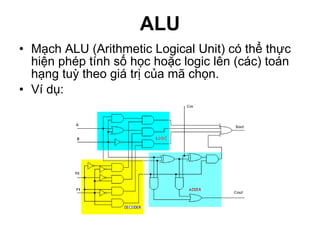
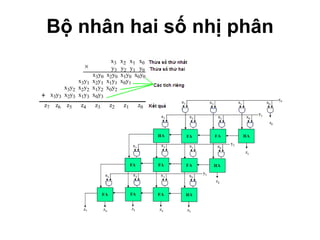
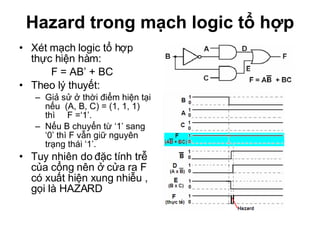
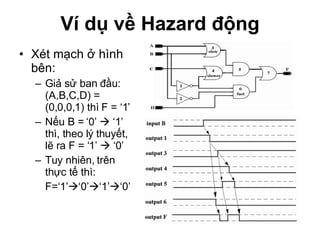
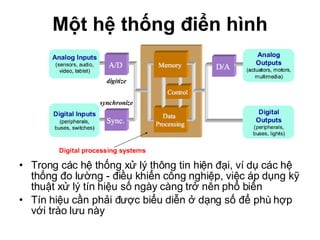
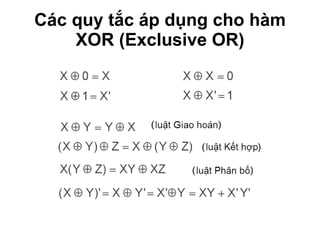Chương 1 của tài liệu trình bày về cách biểu diễn thông tin trong các thiết bị điện tử, nhấn mạnh quá trình biến đổi tín hiệu từ dạng tương tự (analog) sang dạng số (digital) thông qua các bước lấy mẫu và mã hóa. Tài liệu cũng giải thích các hệ thống số như hệ thập phân, nhị phân, và mã BCD, cùng với các phép toán cơ bản và quy tắc xử lý tín hiệu số trong các hệ thống điện tử. Cuối cùng, nó đề cập đến các khái niệm quan trọng như các cổng logic và các quy tắc trong đại số Boole.







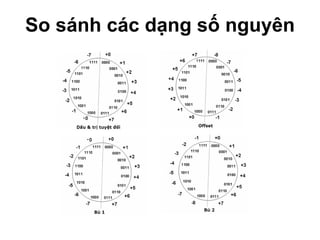
![Tính giá trị của số nguyên Dấu và trị tuyệt đối: I = (-1) b n-1 ×(b n-2 ×2 n-2 + … + b 0 ×2 0 ) Bù 1: b n-1 = 0: I = (b n-2 ×2 n-2 + … + b 0 ×2 0 ) = N b n-1 = 1: I = – [ (1-b n-2 )×2 n-2 +…+ (1-b 0 )×2 0 ] = N – (2 n-1 –1) I = (b n-2 ×2 n-2 + … +b 0 ×2 0 ) – (b n-1 ×2 n-1 –b n-1 ) Bù 2: b n-1 = 0: I = (b n-2 ×2 n-2 + … + b 0 ×2 0 ) = N b n-1 = 1: I = – [ (1-b n-2 )×2 n-2 + … + (1-b 0 )×2 0 +1 ] = N – 2 n-1 I = (b n-2 ×2 n-2 + … +b 0 ×2 0 ) – b n-1 ×2 n-1 Offset: I = (b n-1 ×2 n-1 + b n-2 ×2 n-2 + … + b 0 ×2 0 ) - 2 n-1 = (b n-2 ×2 n-2 + … + b 0 ×2 0 ) – (1 - b n-1 )×2 n-1](https://image.slidesharecdn.com/dientusosld-1211016748669529-8/85/Dientuso-Sld-11-320.jpg)