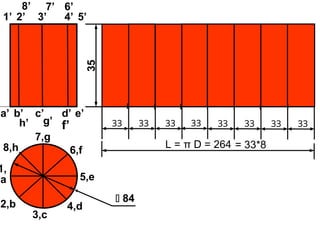
The development of surfaces is the process of creating a flat representation of a three-dimensional object, accurately depicting its true shape and size. This principle is crucial in sheet metal working, with three main methods of development: parallel line, radial line, and triangular development. The parallel line method is specifically applicable to objects with a constant cross-section, such as prisms and cylinders.

1. DEVELOPMENT OF SURFACES

2. DEVELOPMENT OF SURFACES
A layout of the complete surface of a three dimensional object on a plane
surface is called its developments or pattern. Practically the development
consists of drawing the successive surfaces of the object in their true shape
and size with common edges joined. In other word the development of a
geometric solid represents the true shape and size of all its surfaces which
when folded at fold lines, would form the required solid.
The principle of development of surfaces is very much useful in sheet
metal working.

3. There are three methods of developments of surfaces
1. Parallel line development
2. Radial line Development.
3. Triangular Development.
1. Parallel line development : This method can only be used to develop objects
Having a constant cross section for their full length, for example, prisms and
Cylinders and related forms.

6. 20 20 20 20

7. 20 20 20 20
20

8. 20 20 20 20
20

9. 20 20 20 20

10. 20 20 20 20
30

11. 20 10 20 10
30

12. 20 10 20 10
30

13. 30 30 30
50

14. 30 30 30
50

16. 20 20 20
35
20 20

17. 20 20 20
35
20 20 20

18. 33 33 33
35
33 33 33 33 33
a
1,
a’
1’
2,b
3,c
4,d
5,e
6,f
7,g
8,h
b’
2’
c’
3’
d’
4’
e’
5’
f’
6’
g’
7’
h’
8’
 84
L = π D = 264 = 33*8