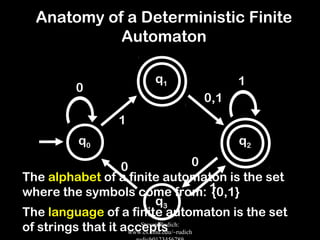
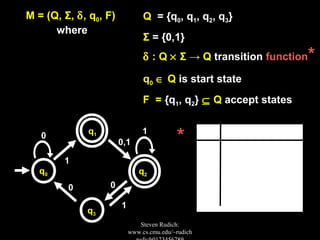
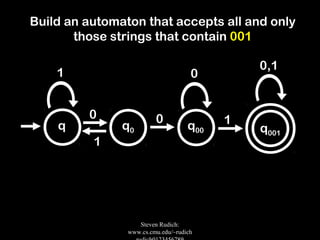
The document discusses deterministic finite automata (DFAs) and regular languages. It provides examples of DFA diagrams and explains how to test if a DFA accepts a given string. It also discusses properties of regular languages, including that they are closed under union, intersection, and negation. The document uses the pigeonhole principle to prove that the language of strings with an equal number of 'a's and 'b's is not a regular language.