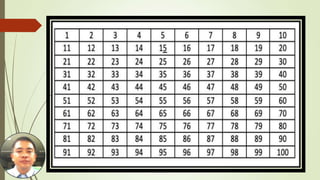
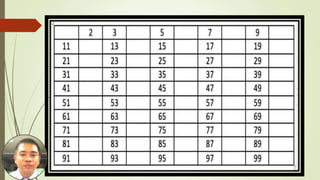
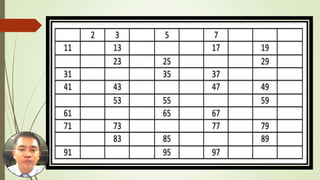
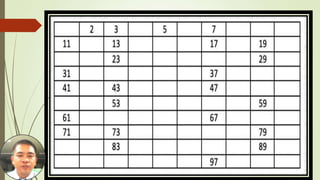
This document discusses prime numbers. It defines a prime number as an integer greater than or equal to 2 that has no positive divisors other than 1 and itself. It then proves two lemmas: 1) an integer n ≥ 2 is composite if and only if it has factors a and b such that 1 < a < n and 1 < b < n; and 2) if n > 1 then there is a prime p such that p | n. It also describes the Sieve of Erastosthenes method for finding all primes up to a given natural number n by listing all integers from 2 to n and marking out multiples of each prime. Finally, it provides an exercise to use this method to find all primes less than