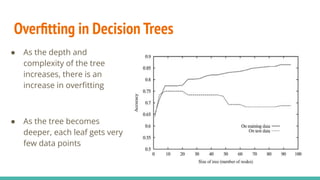
This document discusses decision trees and random forests for classification problems. It provides an overview of how decision trees are trained and make predictions, and how overfitting can be addressed through early stopping techniques. It then introduces random forests, which average the predictions of an ensemble of decision trees to improve accuracy and reduce overfitting compared to a single decision tree. Random forests introduce additional randomness through bagging, where each tree is trained on a random sample of data points and features. This ensemble approach often results in test error reductions even with hundreds or thousands of decision trees.

1. CS189 Discussion 9
Vashisht Madhavan

2. Decision Trees +
Random Forests
Some guidance
with this year’s
election...

3. Decision Trees (Review)
● Nodes represent thresholds
on features
○ I.e. x1 > 3
● Edges lead us to next node
based on threshold
○ I.e. Right if True, Left if False
● Leaf Nodes give us our
predicted class

4. At Test Time
● Start at root node with unlabeled point x
● Descend to leaf node based on feature values of x
● Assign leaf node value as predicted class for x
● Usually O(log n)
○ Worst case O(n)

5. Training a DTree
● How do we decide which features to split on at each level of the tree?
We use this as our
metric for deciding
splits…
Here’s how

6. Training a DTree(cont.)
● We have this idea of Information gain
○ How much does a given feature threshold split reduce our entropy
● So we choose the feature split with the highest information gain
● We need to exhaustively search through values for all features
○ what would be a good way to do this?

7. Discussion Question 1 & 2

8. Overfitting in Decision Trees
● As the depth and
complexity of the tree
increases, there is an
increase in overfitting
● As the tree becomes
deeper, each leaf gets very
few data points

9. Early Stopping ● Prevents Overfitting
● Improves speed
○ Smaller tree
BENEFITS
● We have stopping
criteria to prevent our
tree from growing
further
○ Max Tree Depth
○ Min # of points at
node
○ Tree Complexity
Penalty
○ Validation Error
Monitoring

10. Early Stopping(cont.)
● By stopping early or pruning we do lose some modeling power
○ We cannot capture more complex distributions
Early stopping leads us to
the red line

11. Ensemble Learning
● “Many idiots are often better
than one experts”
● Learn with several algorithms
○ Combine results
● Usually leads to better accuracy
● Very popular with decision trees
○ Random Forests
● Reduces variance
Combination of Decision “Stumps”

12. Random Forests
● Ensemble of short decision trees
● Averaging
○ Randomizing each model
○ I.e. different depth trees
● Bagging
○ Randomize the data fed to each model
○ Take random samples from training data
■ With replacement
● To predict a new sample, we look at whichever class has the most number
of votes from the learners in the ensemble

13. Random Forests(cont.)
● With bagging, trees in the ensemble often look very similar. Why?
○ All trees pick same best splits (“correlated trees”)
○ Averaging won’t help then
● Feature Bagging
○ At each node pick a random subset of m features from d total features
○ Typically m = sqrt(d)
○ Has the effect of “de-correlating” trees in the ensemble
● Sometimes test error reduction up to 100s or even 1,000s of decision
trees!
● Be careful to not dumb down trees too much
○ Ideally want very strong, diverse set of learners in the ensemble

15. Discussion Question 3