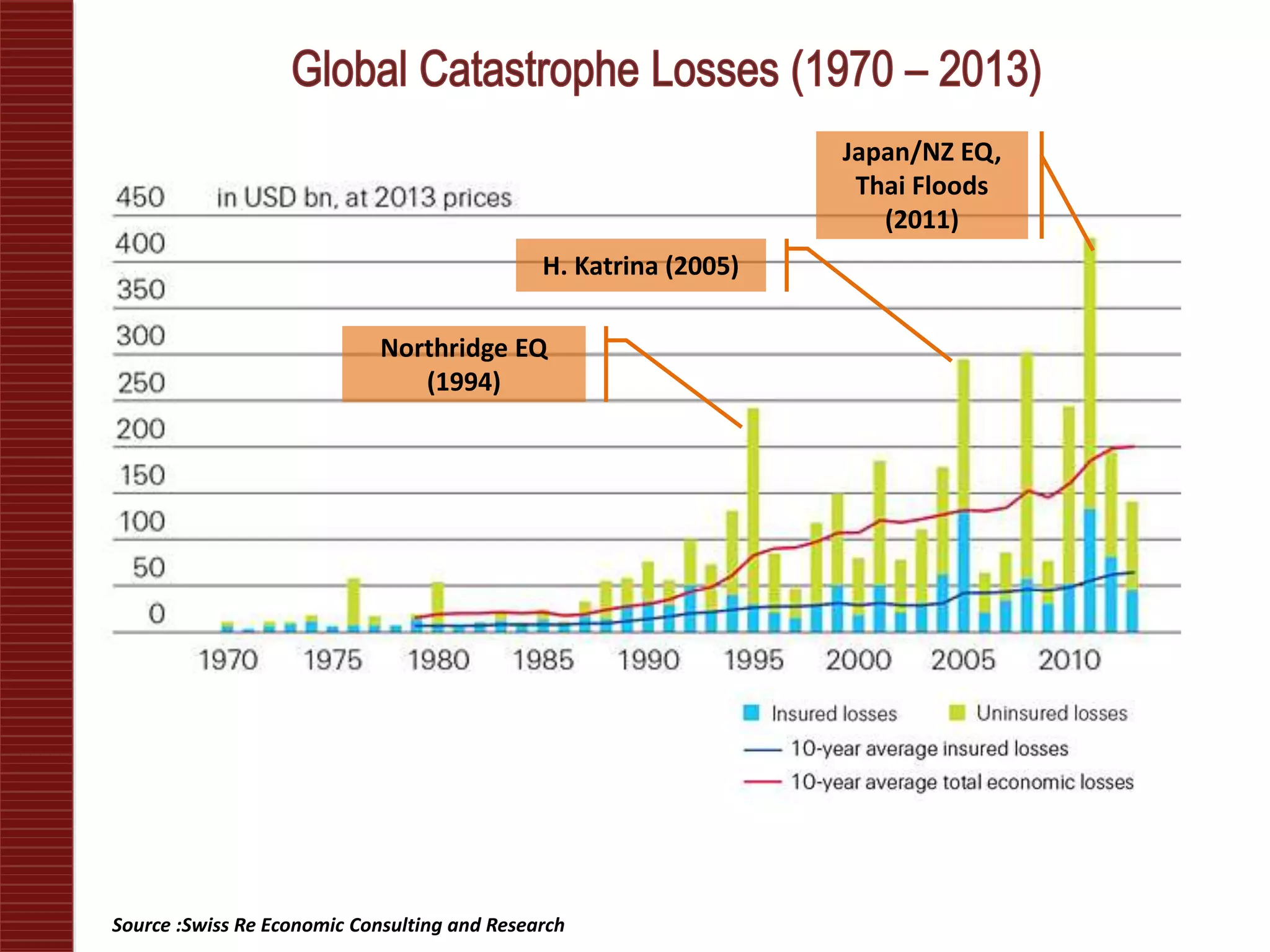
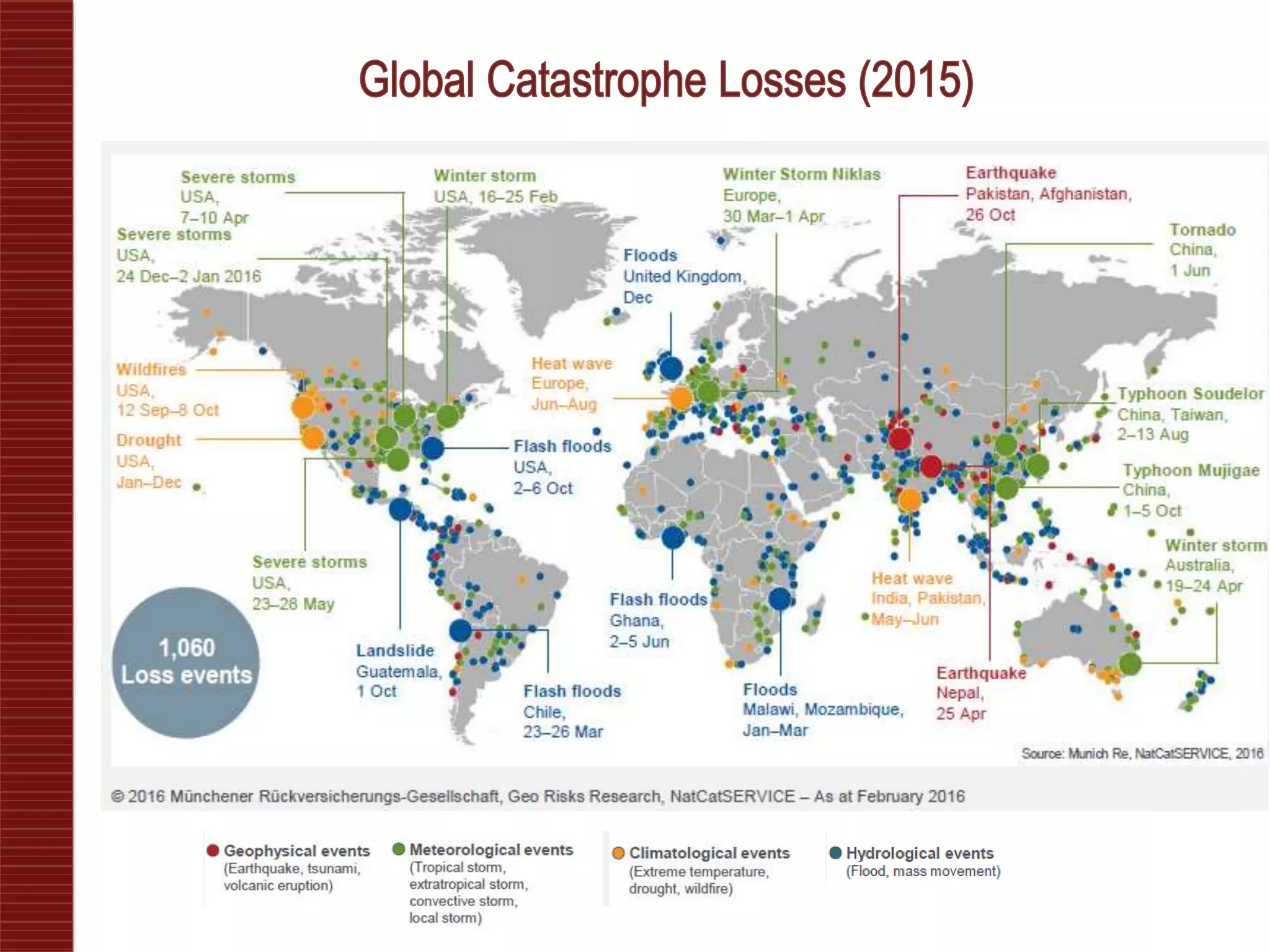
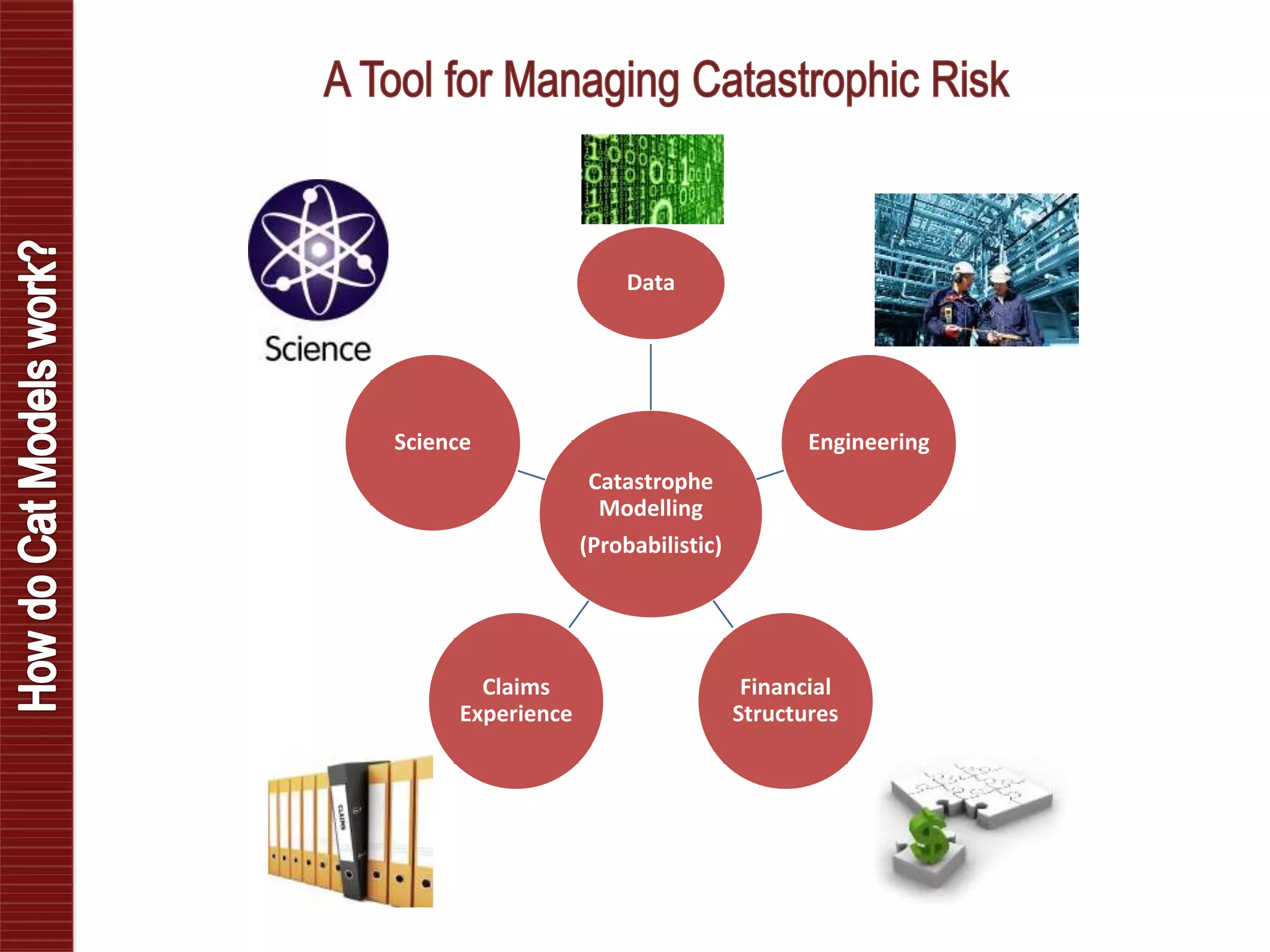
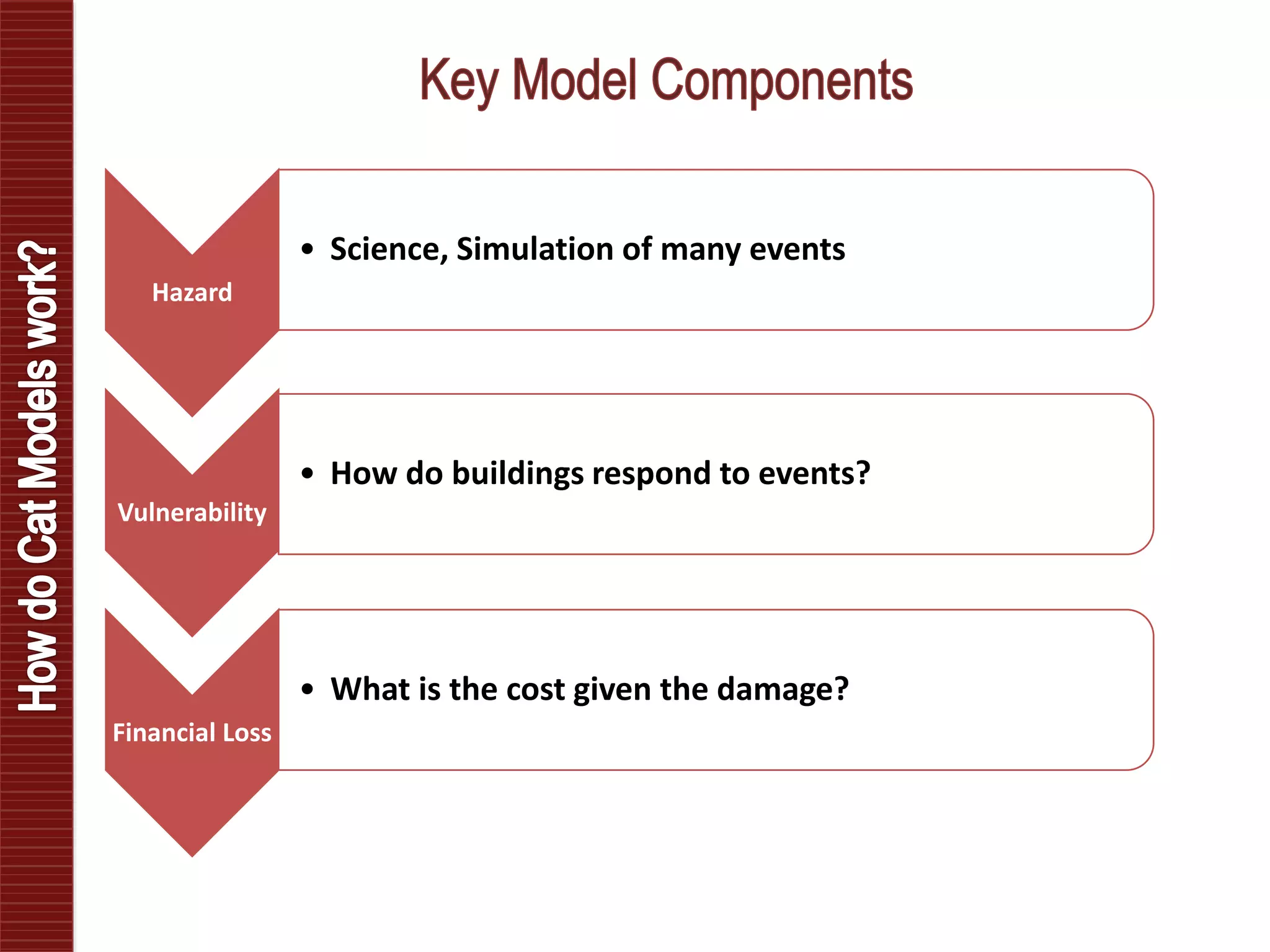
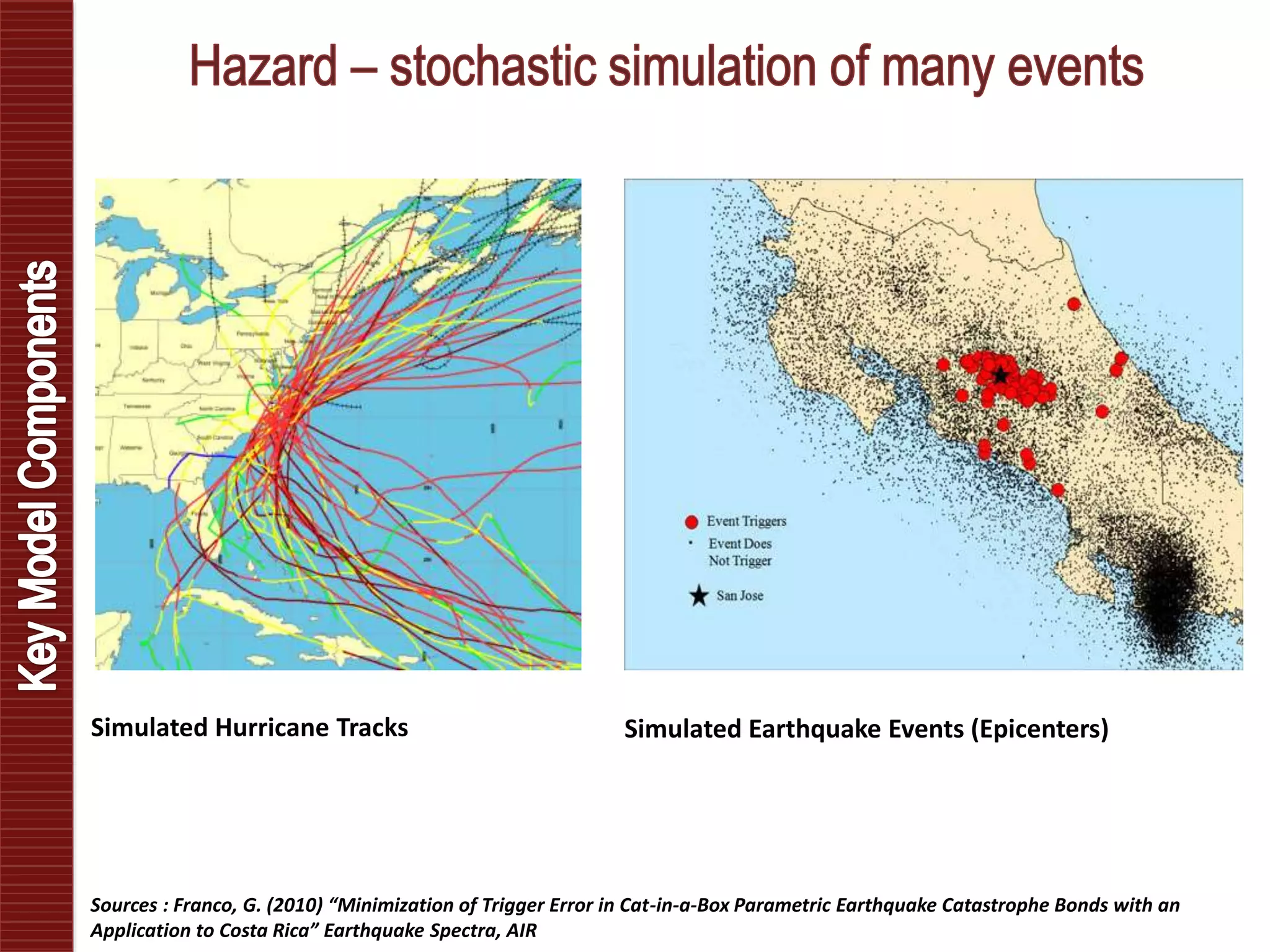
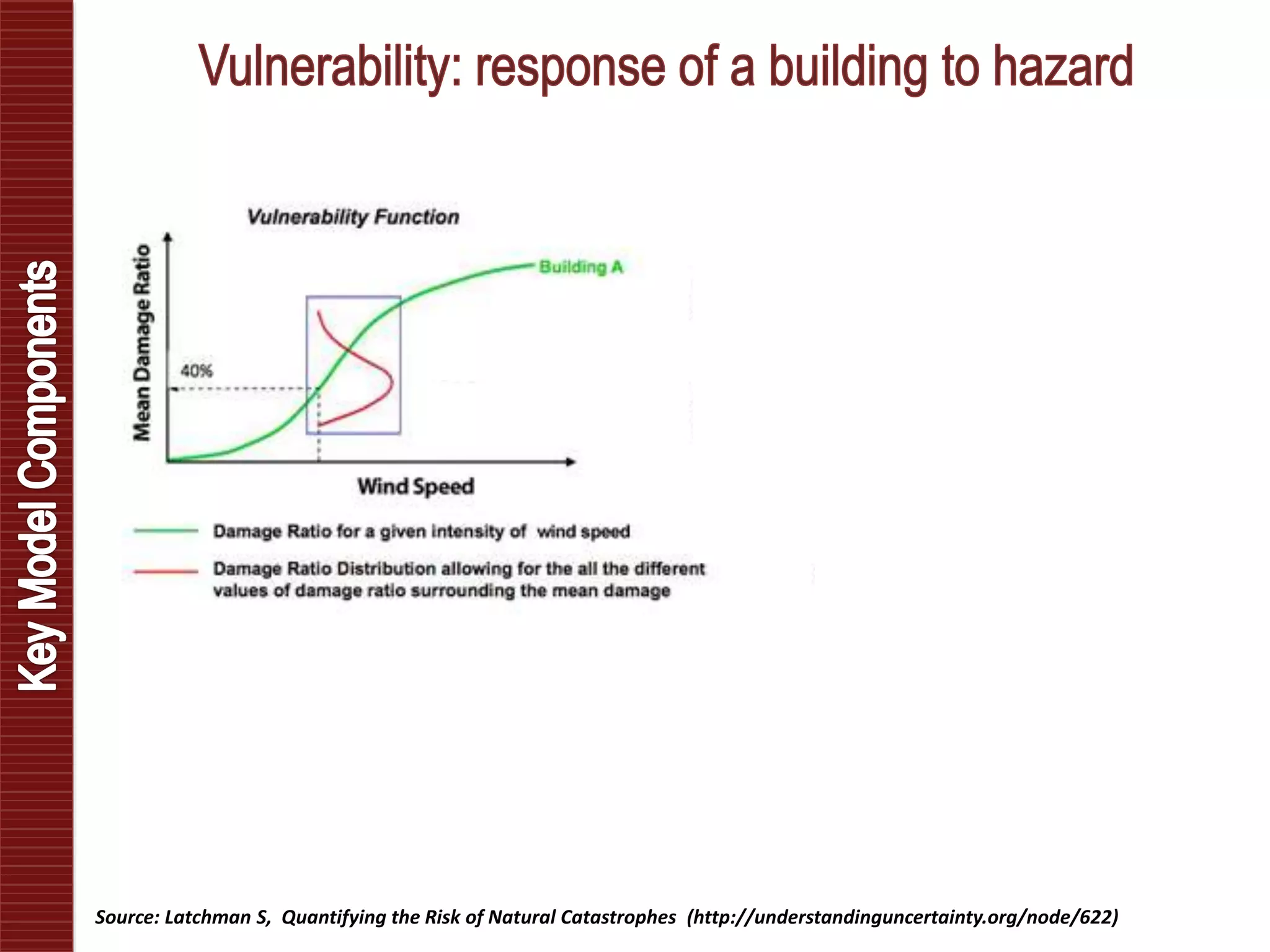
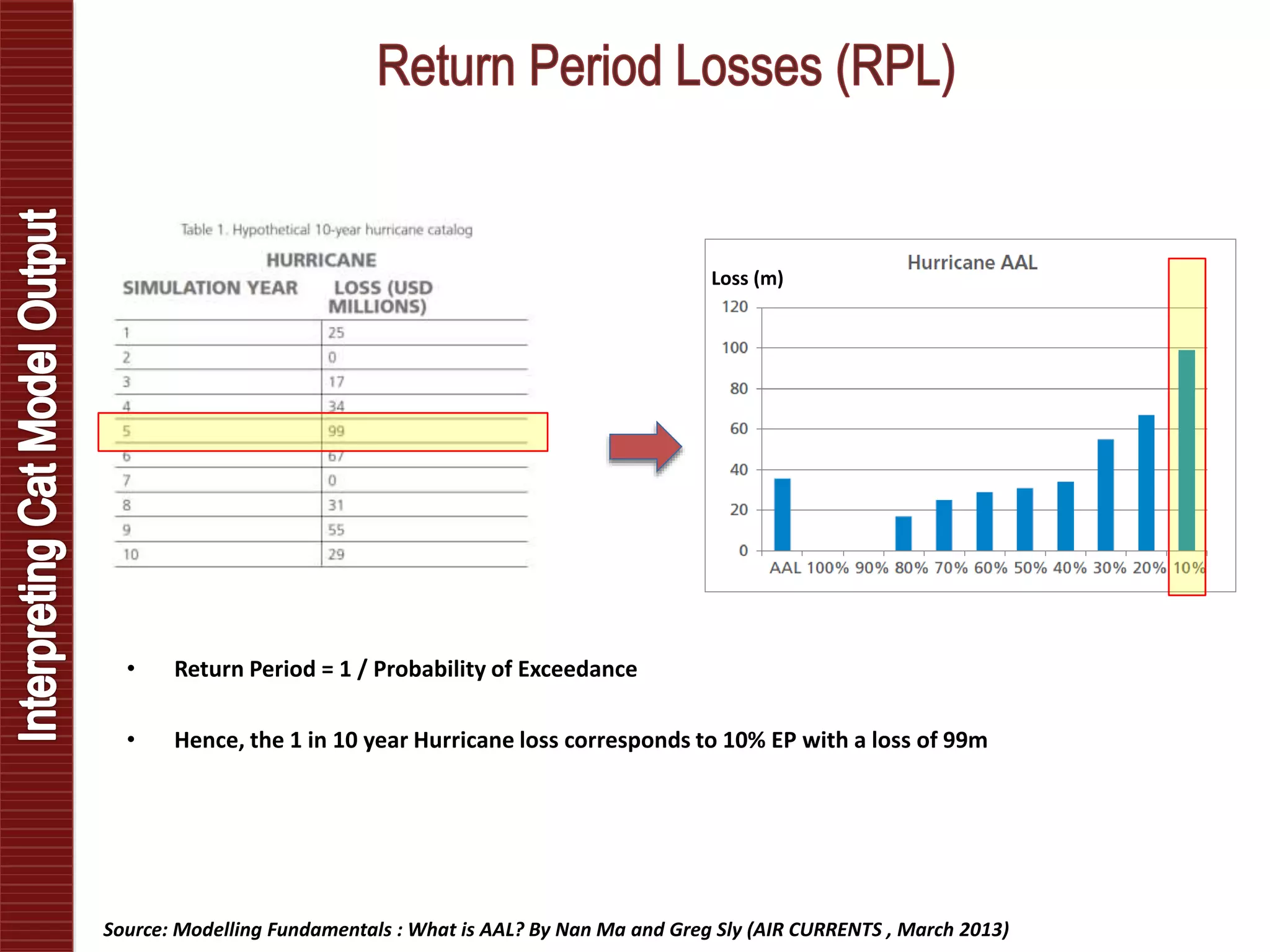
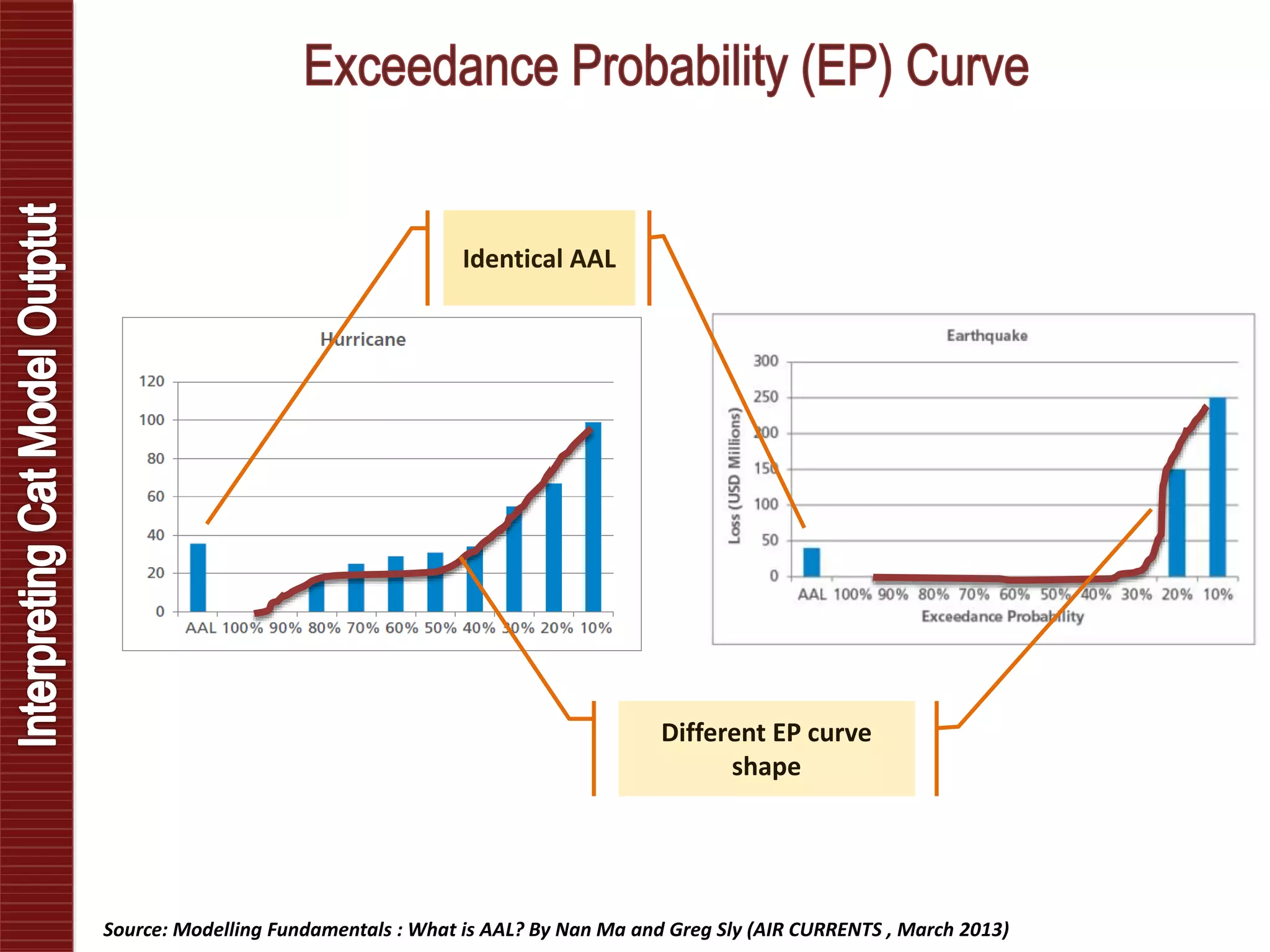
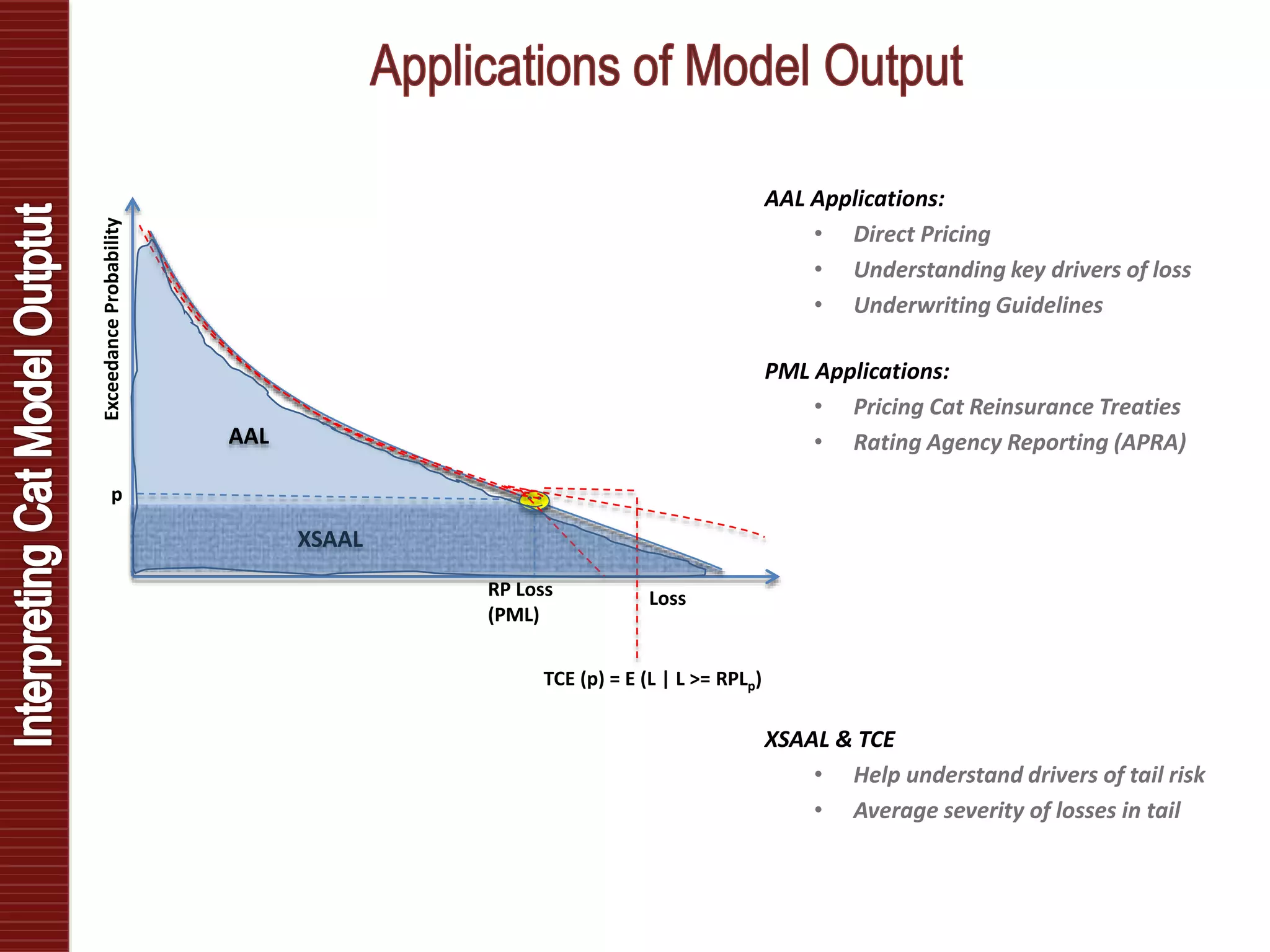
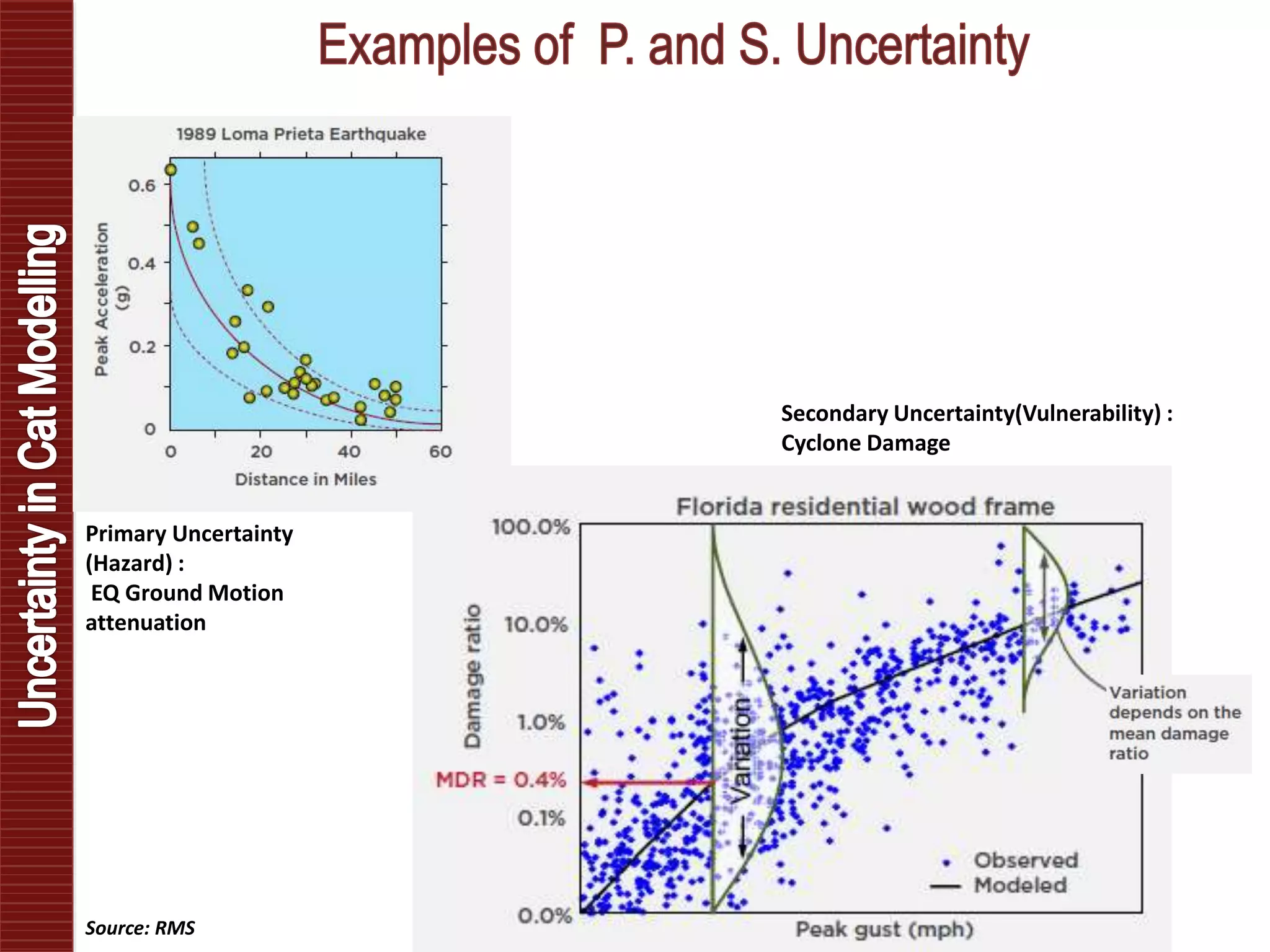
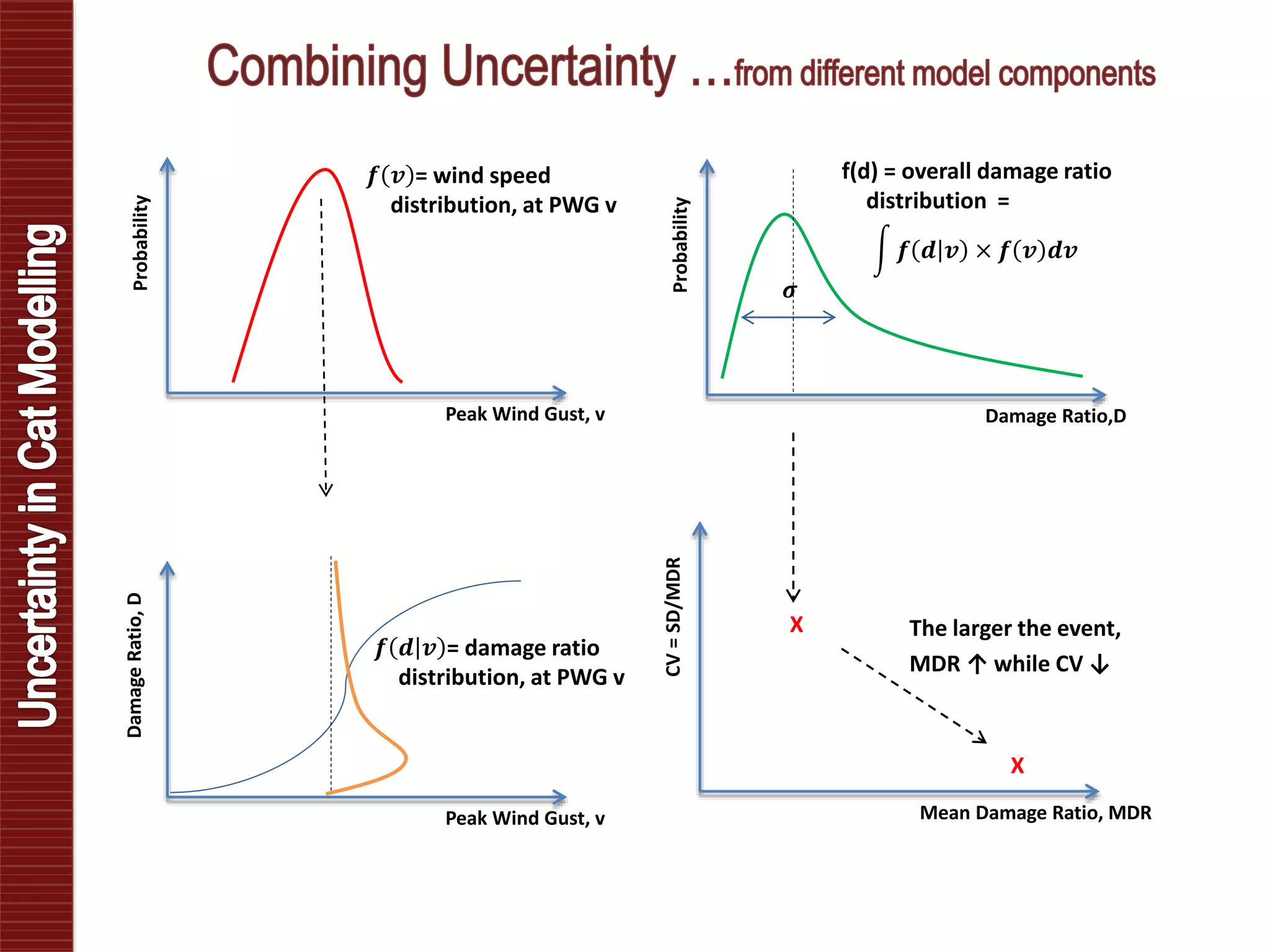
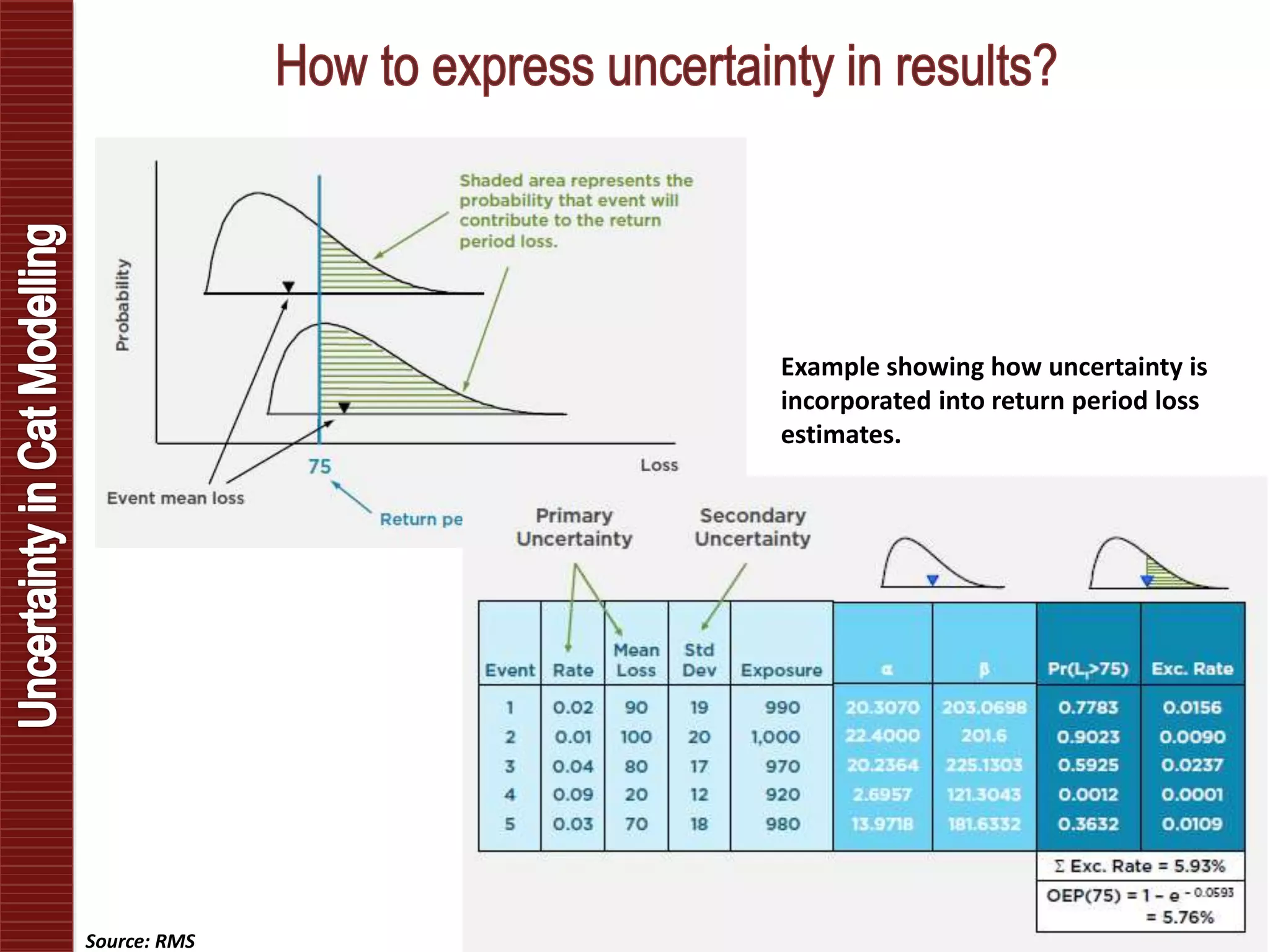
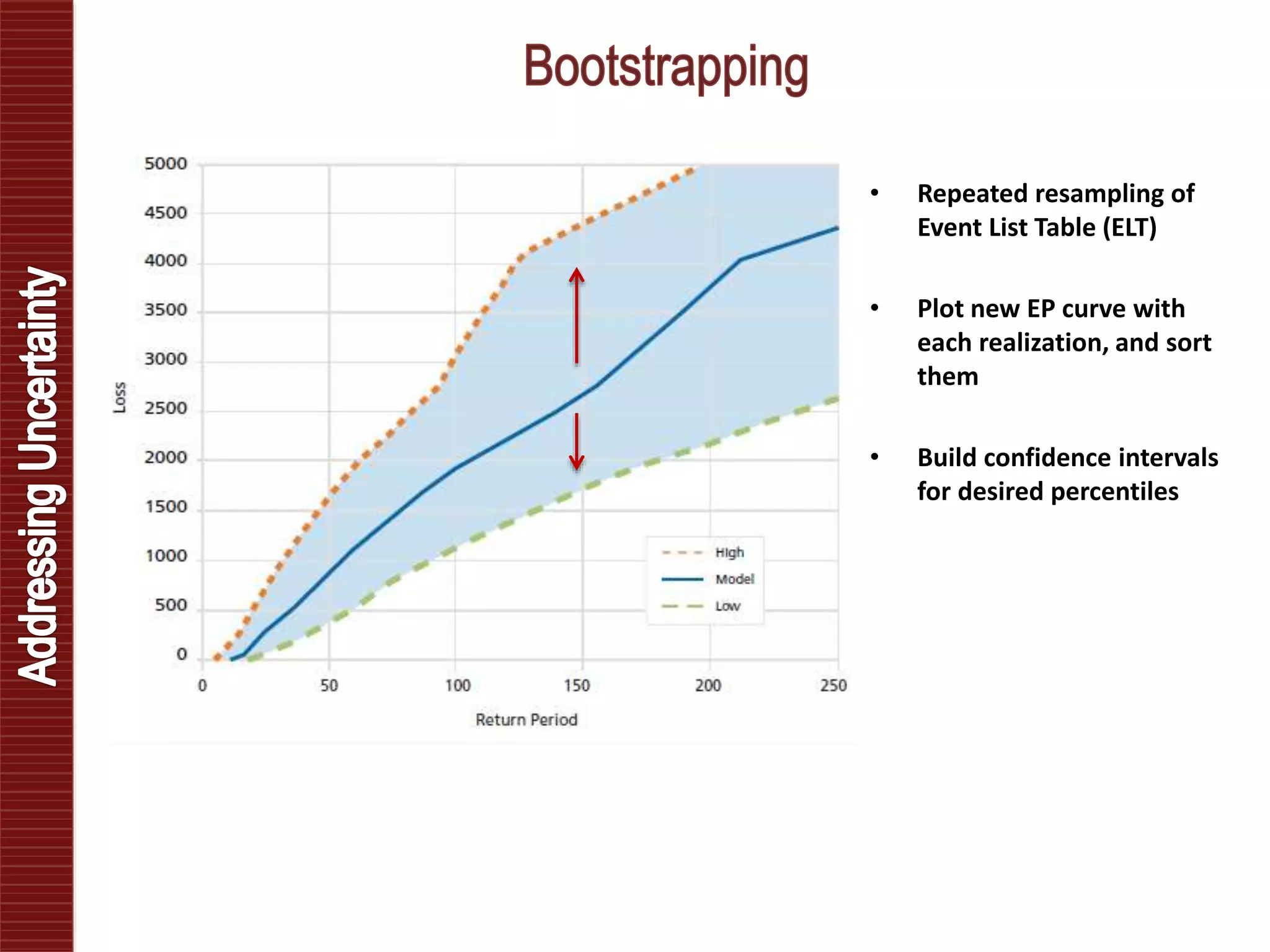
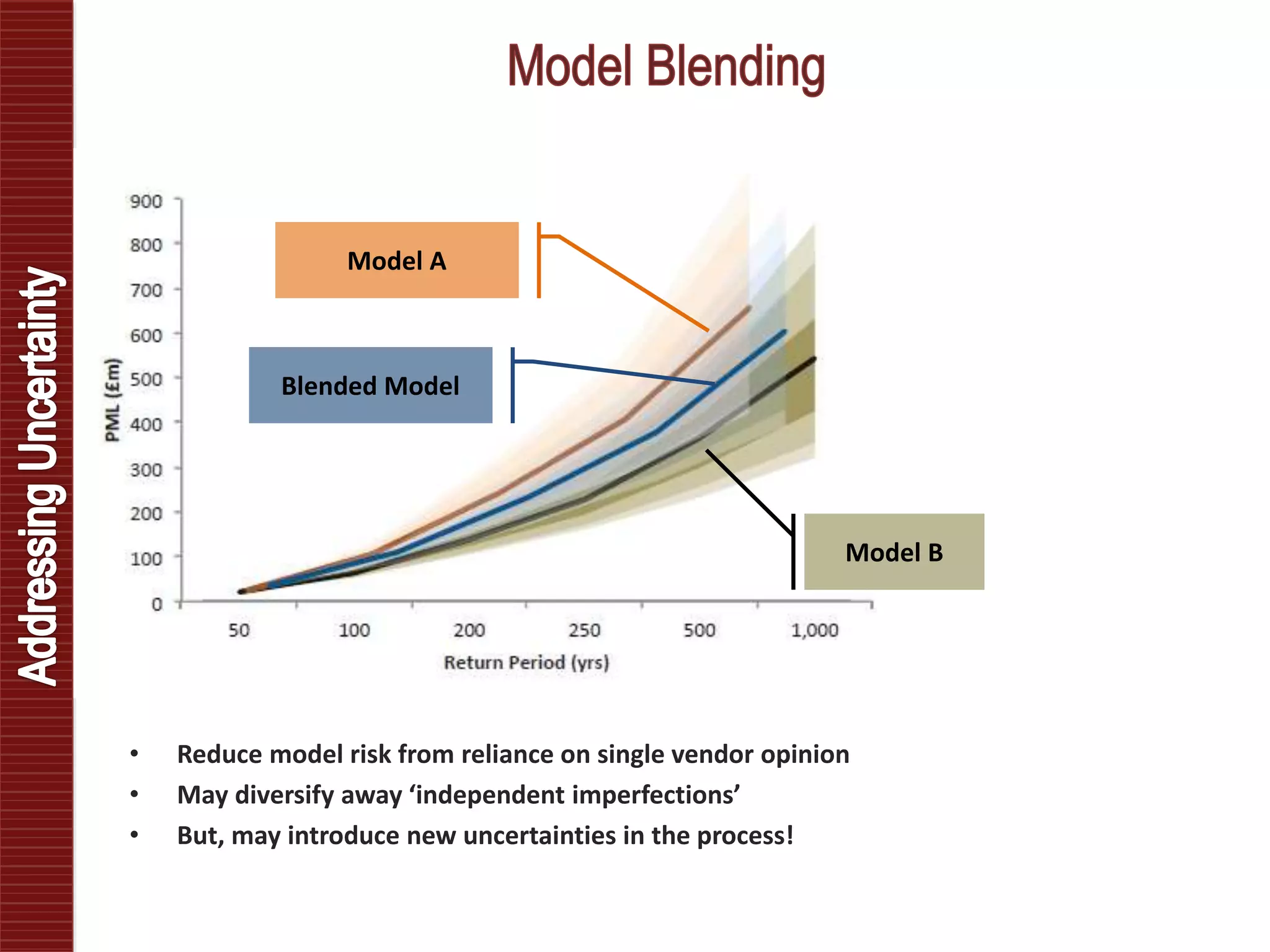
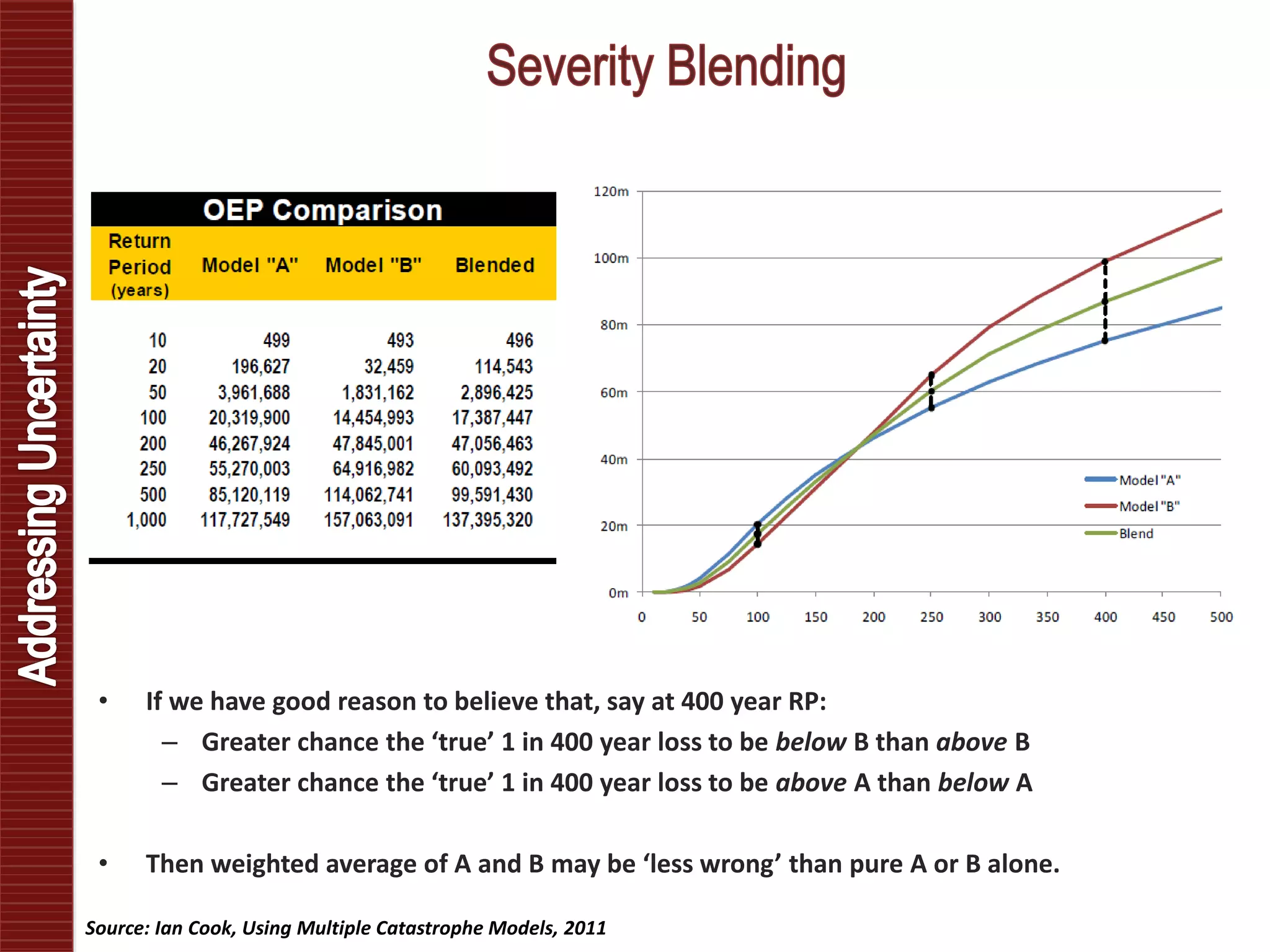
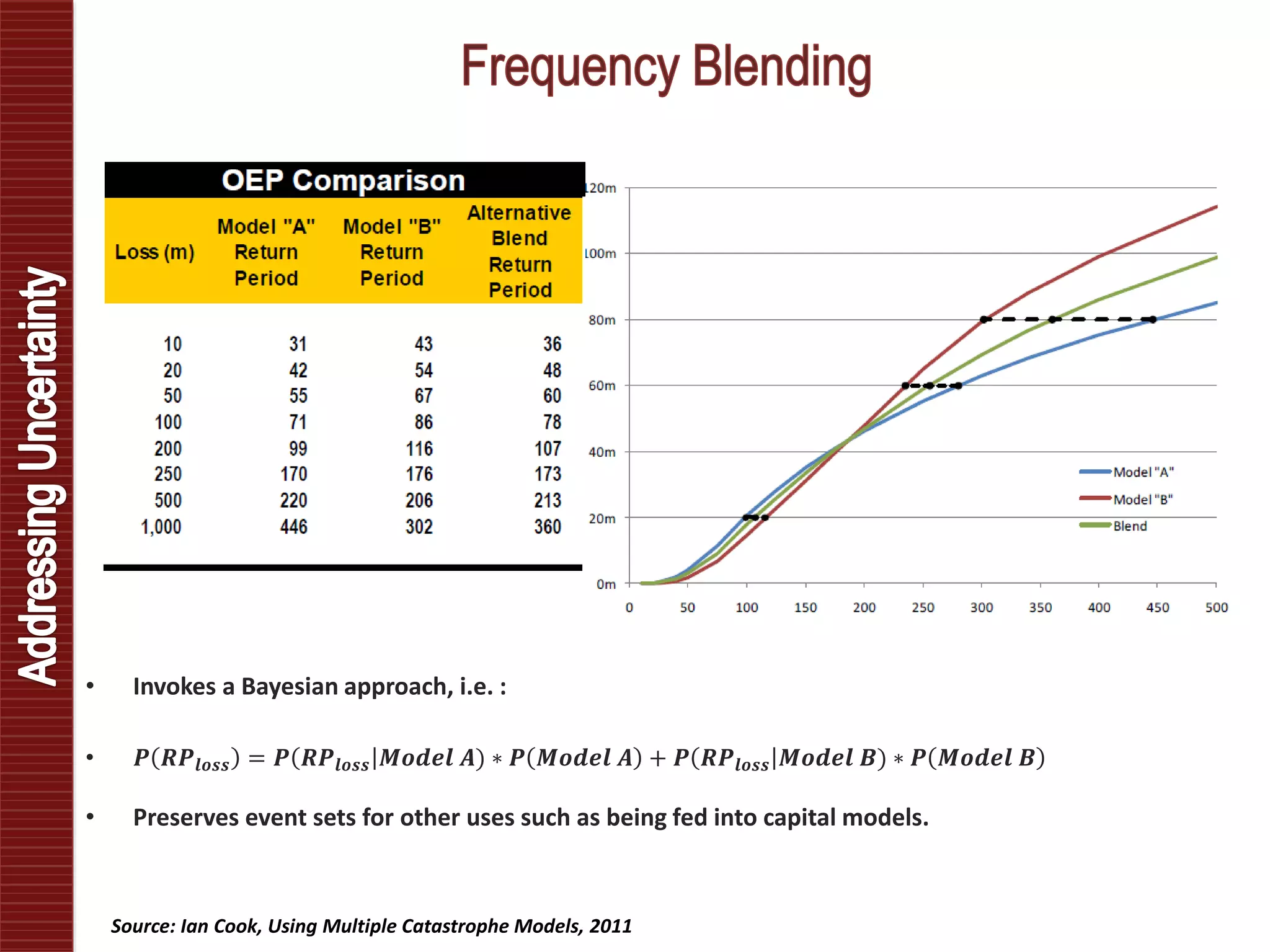
Catastrophe models are used to understand natural disaster risk exposure and aid in pricing and structuring reinsurance programs. The models simulate hazard events and calculate potential financial losses by considering a building's vulnerability and the costs of damage. Key outputs include loss exceedance probabilities, average annual losses, and probable maximum losses. However, there is uncertainty in catastrophe modeling given limitations in data, science, and sampling. Model results are best interpreted as a range rather than a single value.

1. By: Alexander Pui

2. H. Katrina (2005)
Japan/NZ EQ,
Thai Floods
(2011)
Northridge EQ
(1994)
Source :Swiss Re Economic Consulting and Research

4. • Why perform Cat Modelling?
• How do Cat Models work?
• Interpreting Cat Model Output
• Uncertainty in Cat Modelling

5. • Understanding risk exposure
• Direct Pricing
• Structuring and Pricing Reinsurance Programs
• Regulatory Requirements / Dynamic Financial Analysis (DFA)
• Pricing of Alternative Risk Transfer (ART) Mechanisms

6. Catastrophe
Modelling
(Probabilistic)
Data
Engineering
Financial
Structures
Claims
Experience
Science

7. Hazard
• Science, Simulation of many events
Vulnerability
• How do buildings respond to events?
Financial Loss
• What is the cost given the damage?

8. Simulated Hurricane Tracks Simulated Earthquake Events (Epicenters)
Sources : Franco, G. (2010) “Minimization of Trigger Error in Cat-in-a-Box Parametric Earthquake Catastrophe Bonds with an
Application to Costa Rica” Earthquake Spectra, AIR

9. Source: Latchman S, Quantifying the Risk of Natural Catastrophes (http://understandinguncertainty.org/node/622)

10. Wood Frame Masonry

11. Earthquake
MDR
Peak Ground Acceleration
Wood
Frame
Masonry
Cyclone
MDR
Peak Wind Gust
Wood Frame
Masonry

12. • Combined loss distribution for 2 (or more)
buildings in different locations is computed via
convolutions, for each event.
Where:
L = loss of amount L for event
P1(Li) = probability distribution for Location 1
P2(Lj) = probability distribution for Location 2
Li (for P1)
Li + Lj
For e.g. , what is probability of loss of 10m for this event?
Lj (for P2)
Source : Latchman S., Quantifying the Risk of Natural Catastrophes, 2010
𝑷 𝑳 = 𝑷 𝟏 𝑳𝒊 × 𝑷 𝟐 𝑳𝒋

13. • Return Period = 1 / Probability of Exceedance
• Hence, the 1 in 10 year Hurricane loss corresponds to 10% EP with a loss of 99m
Loss (m)
Source: Modelling Fundamentals : What is AAL? By Nan Ma and Greg Sly (AIR CURRENTS , March 2013)

14. • AAL = (250*0.1) + (150*0.1) + (0*0.1) + (0*0.1)...... = 40m
Average Annual Loss (AAL): What is the expected loss from earthquakes this year for Japan EQ?
Source: Modelling Fundamentals : What is AAL? By Nan Ma and Greg Sly (AIR CURRENTS , March 2013)

15. Different EP curve
shape
Identical AAL
Source: Modelling Fundamentals : What is AAL? By Nan Ma and Greg Sly (AIR CURRENTS , March 2013)

16. ExceedanceProbability
Loss
XSAAL
p
RP Loss
(PML)
TCE (p) = E (L | L >= RPLp)
AAL
AAL Applications:
• Direct Pricing
• Understanding key drivers of loss
• Underwriting Guidelines
PML Applications:
• Pricing Cat Reinsurance Treaties
• Rating Agency Reporting (APRA)
XSAAL & TCE
• Help understand drivers of tail risk
• Average severity of losses in tail

17. • Epistemic vs Aleatory Uncertainty
– Epistemic : Imperfect science ; limited historical record; sampling errors
– Aleatory: Intrinsic randomness ; irreducible
• Primary Uncertainty
– Focused more on the hazard generation component
– i.e. event occurrence, parameters that govern cyclone path
• Secondary Uncertainty
– Focused more on vulnerability component
– i.e. ground motions/ wind speeds at site, damage given particular ground
motion/ wind speed.

18. Primary Uncertainty
(Hazard) :
EQ Ground Motion
attenuation
Secondary Uncertainty(Vulnerability) :
Cyclone Damage
Source: RMS

19. CV=SD/MDR
Mean Damage Ratio, MDR
DamageRatio,D
Peak Wind Gust, v
𝒇 𝒅 𝒗 = damage ratio
distribution, at PWG v
Probability
Peak Wind Gust, v
𝒇 𝒗 = wind speed
distribution, at PWG v
Probability
Damage Ratio,D
f(d) = overall damage ratio
distribution =
𝒇 𝒅 𝒗 × 𝒇 𝒗 𝒅𝒗
𝝈
X
X
The larger the event,
MDR ↑ while CV ↓

20. 𝑺𝑫𝒊 𝑺𝑫𝒊+𝟏
. . . .
If Location losses are perfectly correlated (𝐢. 𝐞. , 𝝆 = 𝟏),
𝑺𝑫 𝒕𝒐𝒕𝒂𝒍,𝒄𝒐𝒓𝒓𝒆𝒍𝒂𝒕𝒆𝒅 =
𝒊
𝑵
𝑺𝑫𝒊
𝑺𝑫𝒊
𝑺𝑫𝒊+𝟏
. . . .
If Location losses are perfectly uncorrelated (𝐢. 𝐞. , 𝝆 = 𝟎),
𝑺𝑫 𝒕𝒐𝒕𝒂𝒍,𝒊𝒏𝒅𝒆𝒑𝒆𝒏𝒅𝒆𝒏𝒕 =
𝒊
𝑵
𝑺𝑫𝒊
𝟐+
+
𝑺𝑫 𝒑𝒐𝒓𝒕𝒇𝒐𝒍𝒊𝒐 = 𝒘 ∗ 𝑺𝑫 𝒕𝒐𝒕𝒂𝒍,𝒄𝒐𝒓𝒓𝒆𝒍𝒂𝒕𝒆𝒅 + 𝟏 − 𝒘 ∗ 𝑺𝑫 𝒕𝒐𝒕𝒂𝒍,𝒊𝒏𝒅𝒆𝒑𝒆𝒏𝒅𝒆𝒏𝒕
Hence, overall portfolio standard deviation,
Where w is correlation weights (i.e. more geo-concentrated portfolio will
have larger w than one that is more diverse)

21. Source: RMS
Example showing how uncertainty is
incorporated into return period loss
estimates.

22. • Repeated resampling of
Event List Table (ELT)
• Plot new EP curve with
each realization, and sort
them
• Build confidence intervals
for desired percentiles

23. • Reduce model risk from reliance on single vendor opinion
• May diversify away ‘independent imperfections’
• But, may introduce new uncertainties in the process!
Model A
Model B
Blended Model

24. Source: Ian Cook, Using Multiple Catastrophe Models, 2011
• If we have good reason to believe that, say at 400 year RP:
– Greater chance the ‘true’ 1 in 400 year loss to be below B than above B
– Greater chance the ‘true’ 1 in 400 year loss to be above A than below A
• Then weighted average of A and B may be ‘less wrong’ than pure A or B alone.

25. • Invokes a Bayesian approach, i.e. :
• 𝑷 𝑹𝑷𝒍𝒐𝒔𝒔 = 𝑷 𝑹𝑷𝒍𝒐𝒔𝒔 𝑴𝒐𝒅𝒆𝒍 𝑨) ∗ 𝑷 𝑴𝒐𝒅𝒆𝒍 𝑨 + 𝑷 𝑹𝑷𝒍𝒐𝒔𝒔 𝑴𝒐𝒅𝒆𝒍 𝑩) ∗ 𝑷 𝑴𝒐𝒅𝒆𝒍 𝑩
• Preserves event sets for other uses such as being fed into capital models.
Source: Ian Cook, Using Multiple Catastrophe Models, 2011

26. • Sensitivity testing/ Stress Testing of model assumptions
• Historical Event validation
• Expert Judgment / Consultation with model vendors
• Bias Correction Methods

27. Alexander Pui
Email: alexpui8@gmail.com
Linkedin : https://au.linkedin.com/in/alexander-pui-94a33821