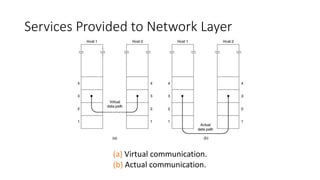
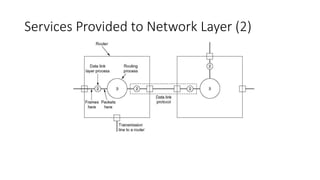
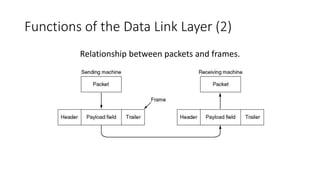
The document discusses various functions and design issues related to the data link layer, including: 1. The data link layer provides services like framing, error control, and flow control to regulate data transmission between network layers. 2. Functions of the data link layer include providing an interface to the network layer, dealing with transmission errors, and regulating data flow to prevent fast senders from swamping slow receivers. 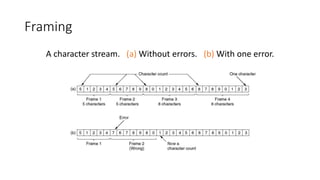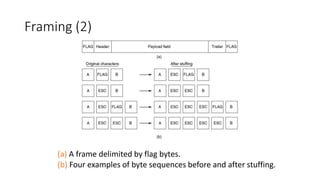3. The document discusses various data link layer techniques for framing, error detection, error correction, and flow control including bit stuffing, parity schemes, CRC schemes, and error-correcting codes.

1. DataLink layer

2. Data Link Layer Design Issues
•Services Provided to the Network Layer
•Framing
•Error Control
•Flow Control

3. Functions of the Data Link Layer
•Provide service interface to the network layer
•Dealing with transmission errors
•Regulating data flow
•Slow receivers not swamped by fast senders

4. Functions of the Data Link Layer (2)
Relationship between packets and frames.

5. Services Provided to Network Layer
(a) Virtual communication.
(b) Actual communication.

6. Services Provided to Network Layer (2)
Placement of the data link protocol.

7. Framing
A character stream. (a) Without errors. (b) With one error.

8. Framing (2)
(a) A frame delimited by flag bytes.
(b) Four examples of byte sequences before and after stuffing.

9. Framing (3)
Bit stuffing
(a) The original data.
(b) The data as they appear on the line.
(c) The data as they are stored in receiver’s memory after
destuffing.

10. Error Detection and Correction
•Error-Correcting Codes
•Error-Detecting Codes
•Key idea: redundant (additional) bits
(use only 2m out of 2n code words)
•Key metrics:
•how many errors can be
corrected/detected;
•what burst length

11. Hamming Distance
•Some codes words are valid; others are invalid
•Hamming distance between two code words is number
of bits that must be flipped to change from one to the
other
• If Hamming distance is d then d single bit errors needed to
change one word to the other
•Hamming distance of a code is the minimum Hamming
distance between two valid code words
•Detecting one single-bit error requires a distance 2
code; how does this generalize?
•Correcting one single-bit error requires a distance 3
code; how does this generalize?

12. Parity Schemes
•Parity bits: choose a rule
• Even parity – each codeword has even number of 1’s
• Odd parity – each codeword has odd number of 1’s
•Always transmit according to the rule
•On receipt, if rule is violated, word is invalid
•Can also do “vertical parity” over whole block to
achieve single-bit error correction

13. CRC Schemes
• CRC – Cyclic Redundancy Check or polynomial code
• Consider bits of a message to be coefficients of a polynomial
M(x)
• 1011 – 1x3 + 0x2 + 1x1 + 1x0
• Of course real messages will be much longer and hence of higher
degree
• Agree on a small-degree generator polynomial G(x) of degree
r
• Note: G(x) has r digits to the right of the leading 1, hence r+1 total
• Divide xrM(x) by G(x) using modulo 2 division (no carries or
borrows) getting the remainder polynomial R(x)
• Transmit T(x) = xrM(x) - R(x); note that this has remainder 0
when divided by G(x)
• Receiver rejects frame if the remainder it computers is not 0

14. Error-Detecting Codes
Calculation of the polynomial code checksum.