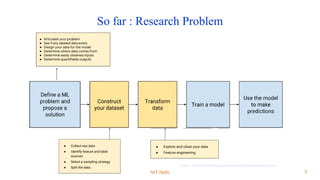
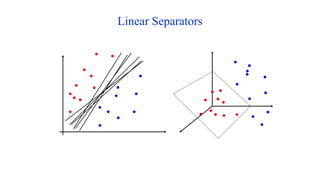
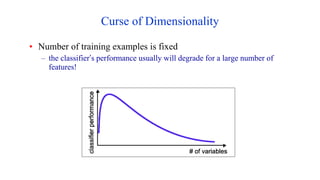
This document discusses module 3 on data pre-processing. It begins with an overview of data quality issues like accuracy, completeness, consistency and timeliness. The major tasks in data pre-processing are then summarized as data cleaning, integration, reduction, and transformation. Data cleaning techniques like handling missing values, noisy data and outliers are covered. The need for feature engineering and dimensionality reduction due to the curse of dimensionality is also highlighted. Finally, techniques for data integration, reduction and discretization are briefly introduced.

![Data Collection and Creation
• Using Already Available data:
– Google Dataset : [ https://datasetsearch.research.google.com/ ]
– Kaggle : [ https://www.kaggle.com/ ]
– UCI Machine Learning Repository : [https://archive.ics.uci.edu/ml/index.php ]
– Paper with code: [ https://paperswithcode.com/ ]
– NLP-progress : [http://nlpprogress.com/]
– Open Government Data (OGD) Platform India [ https://data.gov.in/]
• Other Papers: [https://scholar.google.com/]
• Google Patents : [https://patents.google.com/]
– Why to choose
– Effort of Creating and filtering reduces
– Base Line
– Explore new Computational techniques
– Life easy
3
NIT Delhi](https://image.slidesharecdn.com/3preprocessing-230706103832-dd12f4a7/85/DATA-preprocessing-pptx-3-320.jpg)

























![Pre-processing : Tabular data
• Class Imbalance –
– Synthetic Minority Over-sampling Technique ( SMOTE )
• Example in python
– [Tabular_data.ipynb]
31
NIT Delhi](https://image.slidesharecdn.com/3preprocessing-230706103832-dd12f4a7/85/DATA-preprocessing-pptx-30-320.jpg)










































![Algebraic definition of PCs
.
,
,
2
,
1
,
1
1
1
1 p
j
x
a
x
a
z
N
i
ij
i
j
T
N
p
x
x
x
,
,
, 2
1
]
var[ 1
z
)
,
,
,
(
)
,
,
,
(
2
1
1
21
11
1
Nj
j
j
j
N
x
x
x
x
a
a
a
a
Given a sample of p observations on a vector of N variables
define the first principal component of the sample
by the linear transformation
where the vector
is chosen such that is maximum.](https://image.slidesharecdn.com/3preprocessing-230706103832-dd12f4a7/85/DATA-preprocessing-pptx-74-320.jpg)


























![Normalization
• Min-max normalization: to [new_minA, new_maxA]
– Ex. Let income range $12,000 to $98,000 normalized to [0.0, 1.0].
Then $73,000 is mapped to
• Z-score normalization (μ: mean, σ: standard deviation):
– Ex. Let μ = 54,000, σ = 16,000. Then
• Normalization by decimal scaling
716
.
0
0
)
0
0
.
1
(
000
,
12
000
,
98
000
,
12
600
,
73
225
.
1
000
,
16
000
,
54
600
,
73
104
A
A
A
A
A
A
min
new
min
new
max
new
min
max
min
v
v _
)
_
_
(
'
A
A
v
v
'
j
v
v
10
' Where j is the smallest integer such that Max(|ν’|) < 1](https://image.slidesharecdn.com/3preprocessing-230706103832-dd12f4a7/85/DATA-preprocessing-pptx-101-320.jpg)











