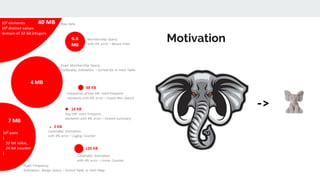
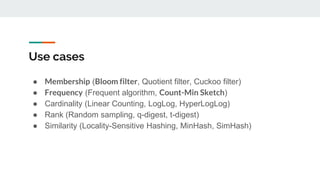
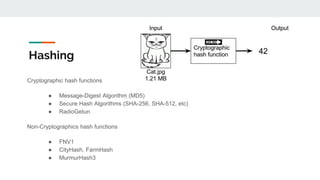
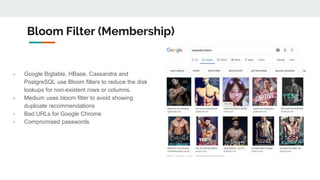
The document discusses various probabilistic data structures, including Bloom filters, count-min sketches, and hashing techniques, highlighting their use cases in data engineering. It outlines their applications in membership checking, frequency counting, cardinality estimation, and similarity detection, showing how they optimize performance and resource usage. The document serves as an introduction to these structures, emphasizing their importance in managing large datasets effectively.

1. Probabilistic data structures

2. https://www.linkedin.com/in/taras-yaroshchuk-551383105/
Taras Yaroshchuk
Senior Data Engineer at Sigma Software
- 4 years in Data Engineering
- AdTech, IoT, FinTech
- Scala/Java/Python
- Trying to contribute to big data community
Skype/Telegram/FB/everywhere: taras.yaroshchuk

3. Use cases
● Membership (Bloom filter, Quotient filter, Cuckoo filter)
● Frequency (Frequent algorithm, Count-Min Sketch)
● Cardinality (Linear Counting, LogLog, HyperLogLog)
● Rank (Random sampling, q-digest, t-digest)
● Similarity (Locality-Sensitive Hashing, MinHash, SimHash)

4. Motivation
->

7. Use cases
● Membership (Bloom filter, Quotient filter, Cuckoo filter)
● Frequency (Frequent algorithm, Count-Min Sketch)
● Cardinality (Linear Counting, LogLog, HyperLogLog)
● Rank (Random sampling, q-digest, t-digest)
● Similarity (Locality-Sensitive Hashing, MinHash, SimHash)

8. Hashing
Cryptographic hash functions
● Message-Digest Algorithm (MD5)
● Secure Hash Algorithms (SHA-256, SHA-512, etc)
● RadioGetun
Non-Cryptographics hash functions
● FNV1
● CityHash, FarmHash
● MurmurHash3
42

9. Bloom Filter (Membership)
- Google Bigtable, HBase, Cassandra and
PostgreSQL use Bloom filters to reduce the disk
lookups for non-existent rows or columns.
- Medium uses bloom filter to avoid showing
duplicate recommendations
- Bad URLs for Google Chrome
- Compromised passwords

10. Bloom Filter (Membership)
- It is like Set(), but doesn’t store elements itself
- Supports 2 operations: add element,
check if element exists
HashSet

11. Bloom Filter (Membership)
0 1 2 3 4
1 0 1 1 0
- It is like Set(), but doesn’t store elements itself
- Supports 2 operations: add element,
check if element exists
- Bit array
- Use multiple hash functions
h1(x) = MurmurHash3(x) % 10
h2(x) = FNV1(x) % 10
HashSet

12. Bloom Filter (Membership)
Example:
- camera on highway
- bad internet connection
- police in 400m

13. Bloom Filter (Membership)
0 1 2 3 4 5 6 7 8 9
0 0 0 1 0 0 0 1 0 0
Euroblyaha detection
QWERTY777, NET1234, ASDF999
1. Add QWERTY777
h1 = MurmurHash3(QWERTY777) % 10 = 7
h2 = FNV1(QWERTY777) % 10 = 3

14. Bloom Filter (Membership)
0 1 2 3 4 5 6 7 8 9
0 0 0 1 0 0 0 1 0 0
Euroblyaha detection
QWERTY777, NET1234, ASDF999
1. Add QWERTY777
h1 = MurmurHash3(QWERTY777) % 10 = 7
h2 = FNV1(QWERTY777) % 10 = 3
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
2. Add NET1234
h1 = MurmurHash3(NET1234) % 10 = 1
h2 = FNV1(NET1234) % 10 = 3

15. Bloom Filter (Membership)
0 1 2 3 4 5 6 7 8 9
0 0 0 1 0 0 0 1 0 0
Euroblyaha detection
QWERTY777, NET1234, ASDF999
1. Add QWERTY777
h1 = MurmurHash3(QWERTY777) % 10 = 7
h2 = FNV1(QWERTY777) % 10 = 3
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
2. Add NET1234
h1 = MurmurHash3(NET1234) % 10 = 1
h2 = FNV1(NET1234) % 10 = 3
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
3. Contains ASDF999? (false)
h1 = MurmurHash3(ASDF999) % 10 = 5
h2 = FNV1(ASDF999) % 10 = 6

16. Bloom Filter (Membership)
0 1 2 3 4 5 6 7 8 9
0 0 0 1 0 0 0 1 0 0
Euroblyaha detection
QWERTY777, NET1234, ASDF999
1. Add QWERTY777
h1 = MurmurHash3(QWERTY777) % 10 = 7
h2 = FNV1(QWERTY777) % 10 = 3
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
2. Add NET1234
h1 = MurmurHash3(NET1234) % 10 = 1
h2 = FNV1(NET1234) % 10 = 3
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
3. Contains ASDF999? (false)
h1 = MurmurHash3(ASDF999) % 10 = 5
h2 = FNV1(ASDF999) % 10 = 6
0 1 2 3 4 5 6 7 8 9
0 1 0 1 0 0 0 1 0 0
4. Contains NET1234? (true)
h1 = MurmurHash3(NET1234) % 10 = 1
h2 = FNV1(NET1234) % 10 = 3

17. Bloom Filter (Membership)
- Element definitely doesn’t exist in the set
- Element may exist in the set. Lets say, 98%

18. Bloom Filter (Membership)
p - positive error rate
m - based on the size of the filter
k - the number of hash functions,
n - number of elements inserted
- Element definitely doesn’t exist in the set
- Element may exist in the set. Lets say, 98%
k m/n p, %
4 6 5.62
6 8 2.15
8 12 0.314
11 16 0.04581 billion elements, p=2% ~ 1 Gb

19. Cassandra
bloom filter

20. How it looks like?
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>22.0</version>
</dependency>

21. How many times element occurred?
Show top X elements
For streaming application that deals with huge amounts of data
● DNS DDoS
● Intent Surge
● twitter trending hashtags
Count-Min Sketch (Frequency)

22. - Use multiple hash functions
- Matrix of counters (not bits)
- Top frequent elements
- Shows upper bound estimation (less than)
Count-Min Sketch (Frequency)
h1(x) = MurmurHash3(x) % 10
h2(x) = FNV1(x) % 10
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 0 0 0 0 0 0
h2 0 0 0 0 0 0 0 0 0 0

23. { ->#quarantine, #quarantine, #brexit, #brexit, #alyonalyona, #quarantine, #tesla, #tesla, #quarantine,
#brexit, #oscar, #quarantine }
Count-Min Sketch (Frequency)
h1(x) = MurmurHash3(x) % 10
h2(x) = FNV1(x) % 10
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 0 0 0 0 0 0
h2 0 0 0 0 0 0 0 0 0 0

24. { #quarantine, #quarantine, -> #brexit, #brexit, #alyonalyona, #quarantine, #tesla, #tesla, #quarantine,
#brexit, #oscar, #quarantine }
Count-Min Sketch (Frequency)
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 2 0 0 0 0 0
h2 0 0 0 0 0 0 0 2 0 0
h1(x) = MurmurHash3(quarantine) % 10 = 4
h2(x) = FNV1(quarantine) % 10 = 7
1. #quarantine
2. #quarantine

25. { #quarantine, #quarantine, #brexit, #brexit, -> #alyonalyona, #quarantine, #tesla, #tesla, #quarantine,
#brexit, #oscar, #quarantine }
Count-Min Sketch (Frequency)
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 2 0 0 0 0 0
h2 0 0 0 0 0 0 0 2 0 0
h1(x) = MurmurHash3(quarantine) % 10 =
4
h2(x) = FNV1(quarantine) % 10 = 7
1. #quarantine
2. #quarantine
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 2 0 0 0 2 0
h2 0 0 2 0 0 0 0 2 0 0
3. #brexit
4. #brexit
h1(x) = MurmurHash3(brexit) % 10 = 8
h2(x) = FNV1(brexit) % 10 = 2

26. { #quarantine, #quarantine, #brexit, #brexit, #alyonalyona, #quarantine, #tesla, #tesla, #quarantine,
#brexit, #oscar, #quarantine -> }
Count-Min Sketch (Frequency)
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 6 0 1 0 5 0
h2 0 0 3 0 0 1 0 6 0 2
h1(x) = MurmurHash3(x) % 10
h2(x) = FNV1(x) % 10 h1(x) = MurmurHash3(brexit) % 10 = 8
h2(x) = FNV1(brexit) % 10 = 2
h1(x) = MurmurHash3(tesla) % 10 = 8
h2(x) = FNV1(tesla) % 10 = 9

27. { #quarantine, #quarantine, #brexit, #brexit, #alyonalyona, #quarantine, #tesla, #tesla, #quarantine,
#brexit, #oscar, #quarantine -> }
Count-Min Sketch (Frequency)
0 1 2 3 4 5 6 7 8 9
h1 0 0 0 0 6 0 1 0 5 0
h2 0 0 3 0 0 1 0 6 0 2
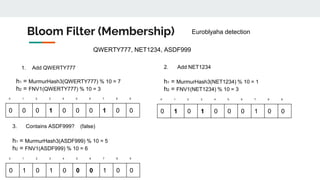
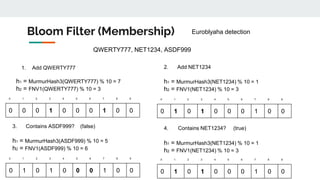
How many times #tesla?
h1(x) = MurmurHash3(tesla) % 10 = 8
h2(x) = FNV1(tesla) % 10 = 9
Final answer = min(h1[8], h2[9]) = min(5, 2) = 2

28. Count-Min Sketch (Frequency)
p = |ln(1/σ)|
m = 2.71828/ɛ
p - number hash functions
σ - standard error
m - number of bits
ɛ - overestimation factor
Example:
We expect to store 10 million of elements
σ should be ~1%, accepted overestimation is
10.
p = |ln(1/0.01)| = 5
ɛ = 10/107=10-6
m = 2.71828/10-6 = 2718280

29. Conclusions
- Probabilistic data structures are not general purpose
- They should be used as optimization
- They can save you memory and time
- Sound complex, but not so scary in practice
- Learn them and impress your interviewer
https://www.amazon.com/Probabilistic-Data-Structures-Algorithms-Applications/dp/3748190484

30. Thanks!