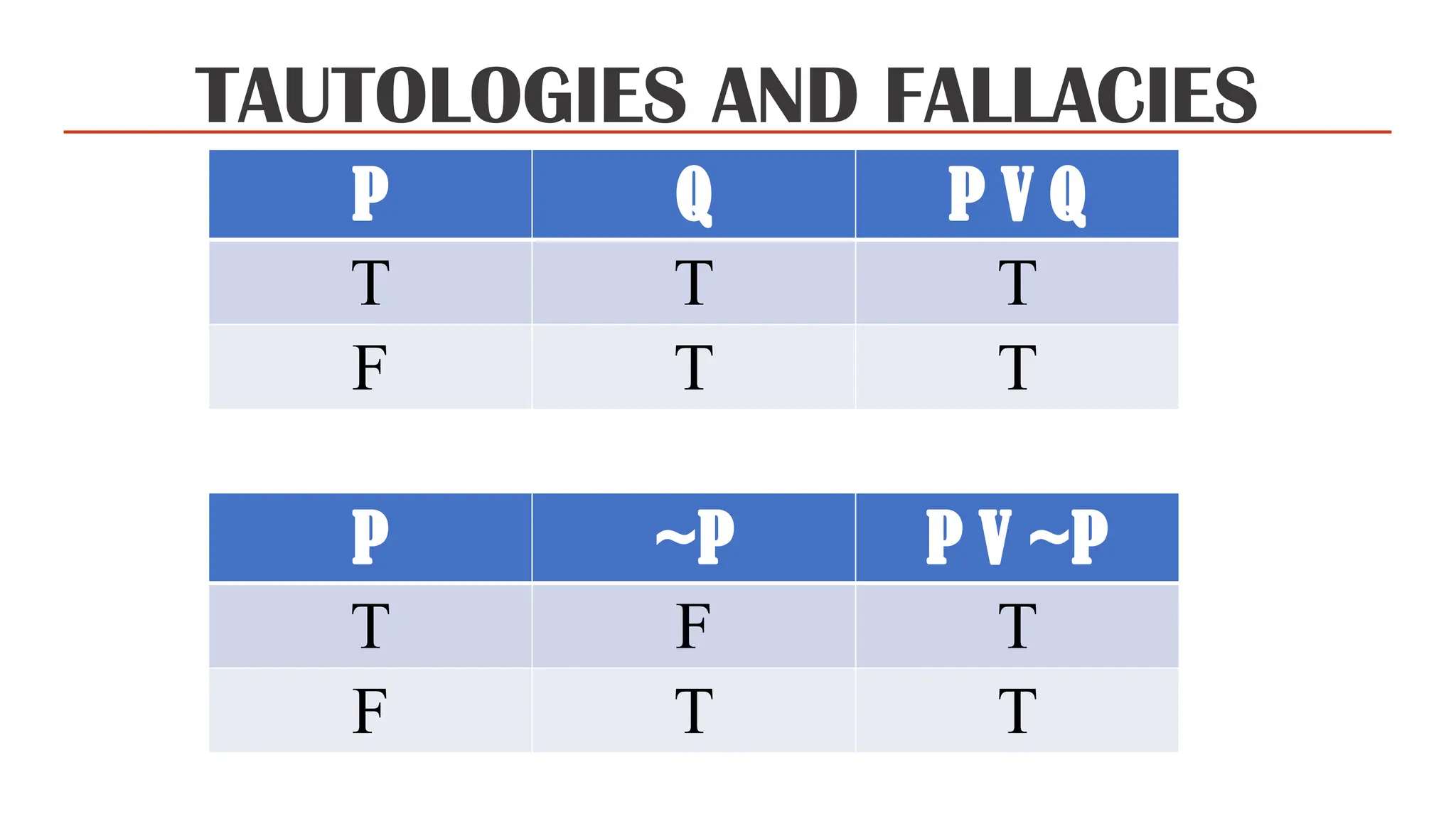
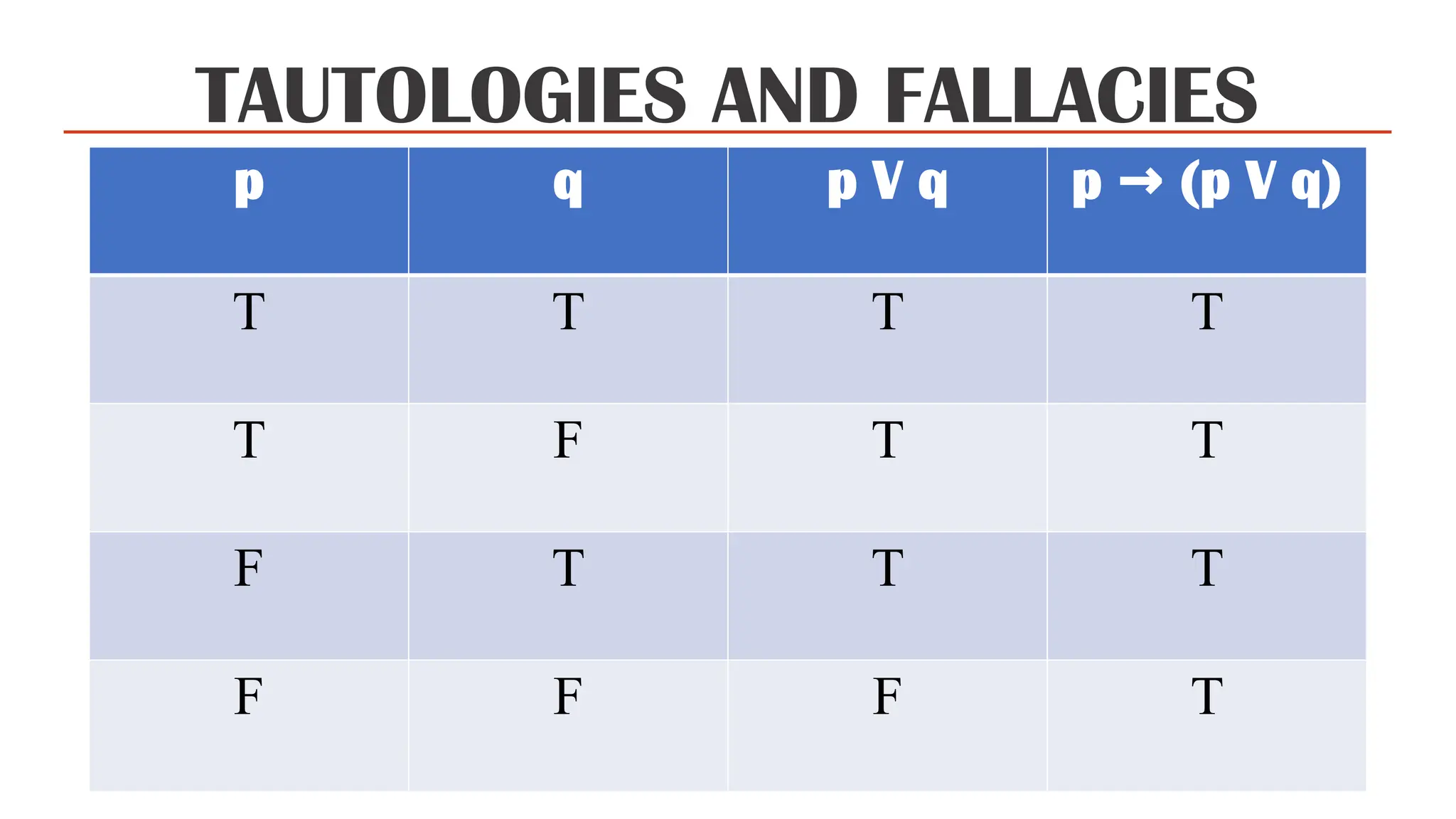
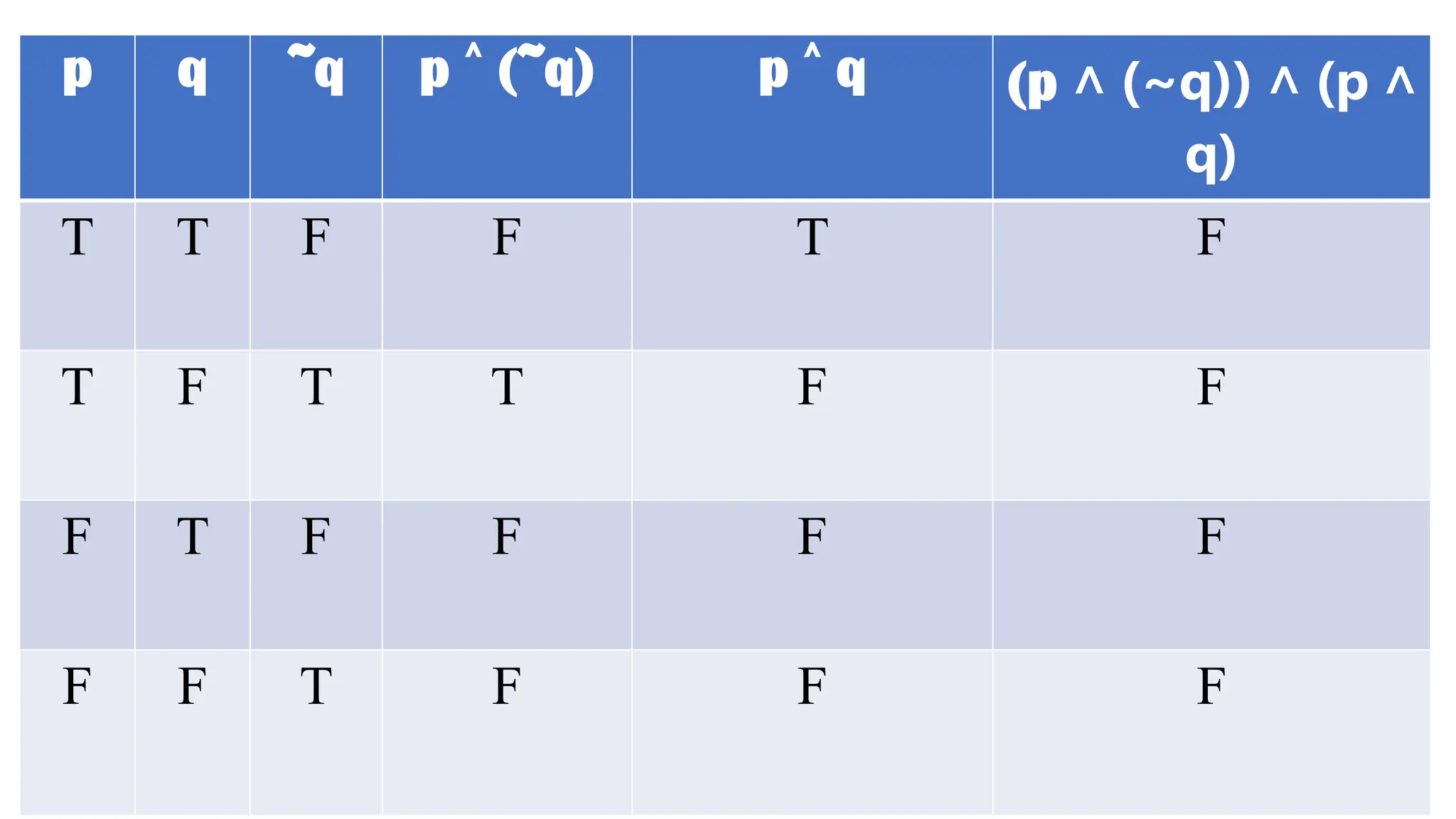
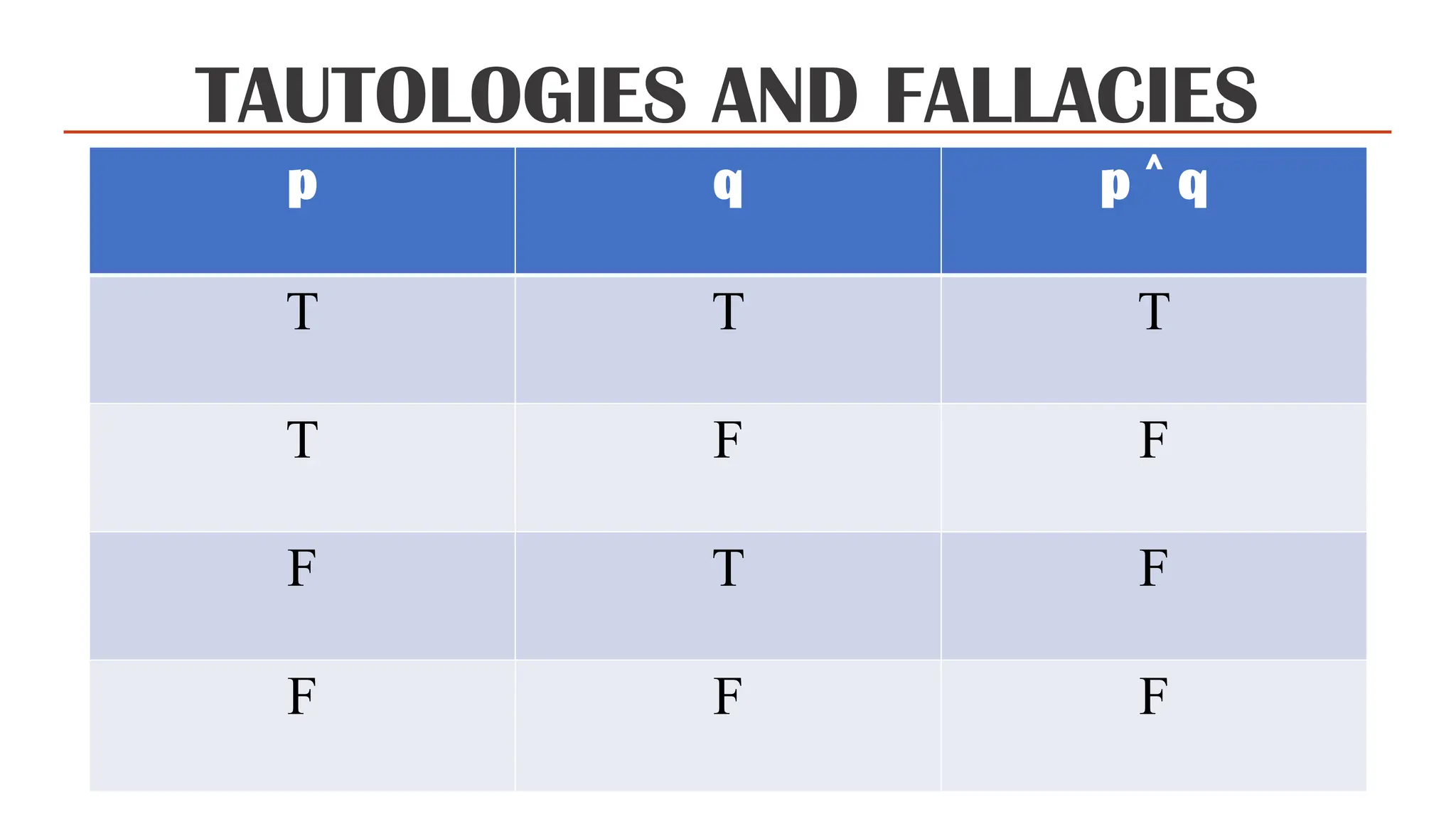
The document discusses conditional propositions, including their forms such as converse, contrapositive, and inverse, and provides examples illustrating these concepts. It defines tautologies, contradictions, and contingencies, explaining their truth values in relation to logic statements. It also differentiates between valid and invalid arguments, outlining the reasoning methods for both along with examples of common fallacies.

1. v

2. v
Tautologies And
Fallacies

3. v
Escanella M.C
Tautologies And
Fallacies
Belga A.B
Branzuela J.M
Aligato I.B
Flor R.E

4. What is a Conditional Proposition?
A compound
statement is a
statement connected
by the words “If…
then” or just “then”

5. If p and q is a conditional proposition ,
we derived three other conditional
statements, namely:
A.Converse: q → p
B.Contrapositive: ~q → ~p
C.Inverse: ~p → ~q

6. Examples:
If Lance is in Grade 11, then he is a
senior high student.
Convert into:
Converse: q → p
Contrapositive: ~q → ~p
Inverse: ~p → ~q

7. Examples:
Converse: q → p
“If Lance is a Senior High School
student, then he is in Grade 11.”
Contrapositive: ~q → ~p
“If Lance is not a Senior High School
student, then he is not in Grade 11.”
NOT NECESSARILY TRUE
TRUE

8. Examples:
Inverse: ~p → ~q
“If Lance is not in Grade 11, then he is
not a Senior High School Student.”
NOT NECESSARILY TRUE

9. Examples:
If she will be given the chance to
perform on stage, then Lea will sing
all her classic songs.
Converse: q → p
Contrapositive: ~q → ~p
Inverse: ~p → ~q

10. Examples:
Converse: q → p
“If Lea will sing her classic songs, then she will
be given the chance to perform on stage.”
Contrapositive: ~q → ~p
“If Lea will not sing her classic songs, then she
will not be given the chance to perform on
stage.”
NOT NECESSARILY TRUE
TRUE

11. Examples:
Inverse: ~p → ~q
“If Lea will not be given the chance to
perform on stage, then Lea will not sing all
her classic songs.”
NOT NECESSARILY TRUE

12. Examples:
If there are no corrupt people, there
are no poor people.
Converse: q → p
Contrapositive: ~q → ~p
Inverse: ~p → ~q

13. Examples:
Converse: q → p
“If there are no poor people, then there are no
corrupt people.”
Contrapositive: ~q → ~p
“If there are poor people, then there are corrupt
people.”
NOT NECESSARILY TRUE
TRUE

14. Examples:
Inverse: ~p → ~q
“If there are corrupt people, there are poor
people.”
NOT NECESSARILY TRUE

15. TAUTOLOGIES AND FALLACIES

16. TAUTOLOGIES AND FALLACIES
P Q P V Q
T T T
F T T
P ~P P V ~P
T F T
F T T

17. TAUTOLOGIES AND FALLACIES
A tautology is a compound statement
that is always true for any combination
of truth values.
A contradiction is a compound
statement that is always false for any
combination of truth values.
A contingency is a proposition that is
neither a tautology nor a contradiction.

18. TAUTOLOGIES AND FALLACIES
p q p V q p (p V q)
→
T T T T
T F T T
F T T T
F F F T

19. TAUTOLOGIES AND FALLACIES
p q ~q p (~q)
˄ p q
˄ (p ˄ (~q)) ˄ (p ˄
q)
T T F F T F
T F T T F F
F T F F F F
F F T F F F

20. TAUTOLOGIES AND FALLACIES
p q p q
˄
T T T
T F F
F T F
F F F

21. TAUTOLOGIES AND FALLACIES
An argument is valid if the conclusion is
true whenever the premises are
assumed to be true.
An invalid argument is also called a
fallacy.

22. REASONS FOR THE VALID ARGUMENT
1. Direct Reasoning or Modus Ponens
2. Contrapositive Reasoning or Modus
Tolens
3. Disjunctive Reasoning or Disjunctive
Syllogism
4. Transitive Reasoning or Hypothetical
Syllogism

23. REASONS FOR THE INVALID ARGUMENT
1. Fallacy of the Converse
2. Fallacy of the Inverse
3. Misuse of Disjunctive Reasoning
4. Misuse of Transitive Reasoning

24. Thank You!