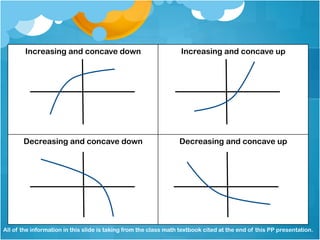
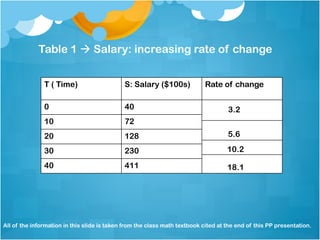
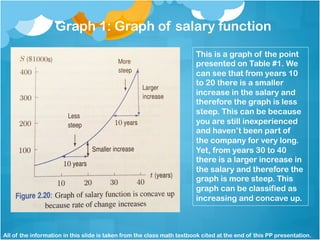
This lesson discusses concavity of graphs and relates it to the rate of change of a function. There are four types of concavity: increasing and concave down, increasing and concave up, decreasing and concave down, and decreasing and concave up. The direction a graph bends depends on whether the rate of change is increasing or decreasing. An example of an increasing concave up graph is a salary function, where salary increases more over time as experience grows.

1. Concavity Lesson
Prof: Ana Maria Lopez

2. Lesson purpose
! Learn about the different concavities of a graph
and relating it to rate of change.
! Explore a real life situation

3. General idea
! Because the rate of change changes when X
increases or decreases, the slope of a graph
changes as well as X increases/decreases, so
the graph bends upward if it increases or
upward decreases.
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

4. Four possible concavities
! Increasing and concave down
! Increasing and concave up
! Decreasing and concave down
! Decreasing and concave up
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

5. Increasing and concave down Increasing and concave up
Decreasing and concave down
Decreasing and concave up
All of the information in this slide is taking from the class math textbook cited at the end of this PP presentation.

6. Important!
! “If F is a function whose rate of change increases
(Gets less negative or more positive as we move
from left to right), then the graph of F is concave up.
In this case, the graph bends upward”
! “If F is a function whose rate of change decreases
(Gets less positive or more negative as we move
from left to right), then the graph of F is concave
down. In this case, the graph bends downwards”.
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

7. Real life example!
! When you eventually work and get a salary that
increases, this function would create an
increasing graph, meaning it would be concave
up.
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

8. Table 1 à Salary: increasing rate of change
T ( Time) S: Salary ($100s) Rate of change
0 40
10 72
20 128
30 230
40 411
3.2
5.6
10.2
18.1
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

9. Graph 1: Graph of salary function
This is a graph of the point
presented on Table #1. We
can see that from years 10
to 20 there is a smaller
increase in the salary and
therefore the graph is less
steep. This can be because
you are still inexperienced
and haven’t been part of
the company for very long.
Yet, from years 30 to 40
there is a larger increase in
the salary and therefore the
graph is more steep. This
graph can be classified as
increasing and concave up.
All of the information in this slide is taken from the class math textbook cited at the end of this PP presentation.

10. Sources
! Hughes-Hallett, Deborah, Andrew M. Gleason,
and Et. Al. "Ch 2.5: Concavity." Functions
Modeling Change: A Preparation for Calculus. By
Eric Connally. 4th ed. N.p.: John Wiley & Sons,
2011,2006,2003. 93-97. Print.