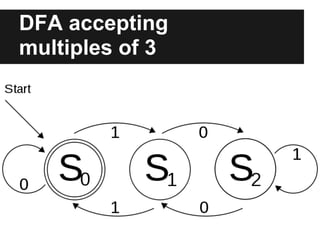
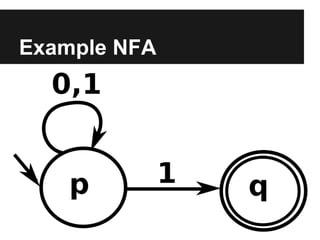
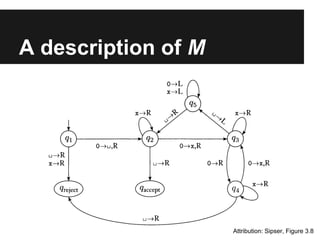
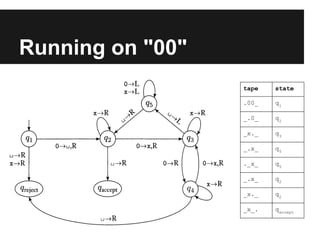
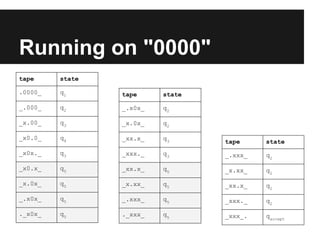
This document provides an introduction to foundational concepts in computer science including Turing machines. It defines key terms like alphabet, string, formal language, deterministic finite automata, nondeterministic finite automata, regular expressions, and Turing machines. It also presents examples of each concept and shows how a Turing machine can recognize strings of a given length.

1. Computer
Science
Foundations
Turing Machine Edition
Jason Dew
Geezeo / Catamorphic Labs

2. Alan
Turing

3. Entscheidungsproblem
David
Hilbert

4. Alphabet
any set of symbols
examples:
● {a, b, c, d, ..., z}
● {0, 1, 2, 3, ..., 9}
● {0, 1}

5. String
sequence of symbols from the alphabet
examples:
● foobar
● 0101001
● (empty string)

6. Formal Language
any set of strings over an alphabet
examples:
● {foo, bar, baz}
● {00, 01, 10, 11}
● {b, ab, aab, aaab, aaaab, ... }

7. Deterministic
Finite Automata
http://15mmvsf.bagofmice.com/vsf/prev_robot.htm

8. Formal Definition
● an alphabet
● a set of states
○ one denoted as a "starting state"
○ one or more denoted as "accepting states"
● a transition function
○ takes a symbol and a state and returns a new state

9. DFA accepting
multiples of 3

10. Nondeterministic
Finite Automata

11. Formal Definition
● an alphabet
● a set of states
○ one denoted as a "starting state"
○ one or more denoted as "accepting states"
● a transition function
○ takes a symbol and a state and returns
zero or more states

12. Example NFA

13. Theorem
Any NFA can be converted
into an equivalent DFA.

14. Regular Language
Any language which
can be recognized by
some finite automaton.

15. Regular Expressions

16. Theorem
A language is regular
if and only if
some regular expression
describes it.

17. Turing machines

18. Formal Definition (slightly simplified)
● two alphabets
○ one for reading, the input alphabet
○ one for writing, the output (or tape) alphabet
● a set of states
○ one starting state
○ one accepting state
○ one rejecting state
● a transition function
takes a symbol and a state and returns
a new state, a symbol to write, and Left or Right

19. Example TM
Let's call it M
It accepts strings whose length is a power of 2
Accepted strings: "0", "00", "0000"
Rejected strings: "", "000", "000000"

20. A description of M
Attribution: Sipser, Figure 3.8

21. Running on "00"
tape state
.00_ q1
_.0_ q2
_x._ q3
_.x_ q5
._x_ q5
_.x_ q2
_x._ q2
_x_. qaccept

22. Running on "0000"
tape state
.0000_ q1 tape state
_.000_ q2 _.x0x_ q2
_x.00_ q3 _x.0x_ q2
_x0.0_ q4 _xx.x_ q3
tape state
_x0x._ q3 _xxx._ q3 _.xxx_ q2
_x0.x_ q5 _xx.x_ q5 _x.xx_ q2
_x.0x_ q5 _x.xx_ q5 _xx.x_ q2
_.x0x_ q5 _.xxx_ q5 _xxx._ q2
._x0x_ q5 ._xxx_ q5 _xxx_. qaccept

23. Wrapping up
Why do we care about
Turing machines?

24. References
Deterministic finite automaton. (2012, March 11). Retrieved from http://en.wikipedia.
org/wiki/Deterministic_finite_automaton
Nondeterministic finite automaton. (2012, April 20). Retrieved from http://en.
wikipedia.org/wiki/Nondeterministic_finite_automaton
Petzold, C. (2008). The annotated turing. Indianapolis: Wiley Publishing, Inc.
Sipser, M. (2006). Introduction to the theory of computation. (2nd ed.). Boston:
Thompson Course Technology.
Turing machine. (2012, April 17). Retrieved from http://en.wikipedia.
org/wiki/Turing_machine

25. Come work with me!