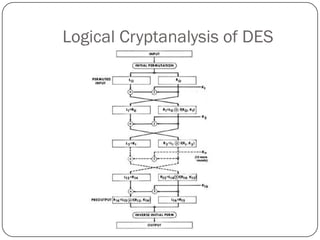
This document discusses combinatorial design problems and approaches to solving them. It introduces combinatorial problems and challenges like huge search spaces. Methods covered include modeling problems as constraint satisfaction problems (CSPs) and using constraint propagation to reduce the search space. Specific problems discussed include ternary Steiner systems, Hamming distance optimization, and modeling the Data Encryption Standard (DES) cipher as a SAT problem for cryptanalysis.

1. Combinatorial Design Problems

2. Outline
Introduction
What are combinatorial problems ?
Challenges
Real life Problems
Solving combinatorial problems
Reducing combinatorial problems
Modeling as
Constraint satisfaction problem
Subset generation problem
Satisfaction problem
Error correcting & Cryptology
Hamming Distance Problem
Logical Cryptanalysis of DES

3. What are combinatorial problems ?
A class of problems that are at least NP:
Enumerative combinatorics
Counting the number of certain combinatorial objects
How many ways are there to make a 2-letter word?
How many ways are there to select 5 integers from {1,..,20} such that the (positive) difference between any 2 of the 5 integers is at least 3?
Design Theory
Study of combinatorial design, which are collection of subsets with certain intersection properties
Ternary Steiner systems
oSelect 3-element subsets from the set {0,1,2,3,4,5,6} such that each object occurs in 3 of the subsets and the intersection of every two subsets has precisely one member.
Graph theory, Order theory, Geometric combinatorics, …etc.

4. What are combinatorial problems ?
Characteristics & Challenges
Most of these problems are classified as NP problems
Huge search space
Real combinatorial problems
Cryptography / Error Correcting
Finding Shortest round trips (TSP)
Boolean satisfaction problems (SAT)
Planning, scheduling & timetabling
Protein structure prediction
Internet packet data routing , …etc.

5. Solving combinatorial design problems
Reducing combinatorial design problems
Need to prune search space before actually searching
Get results in reasonable time
How can this be done ?
Constraint programming
Model problem as a constraint satisfaction problem (CSP)
o(V,D,C)
oV is a set of variables taking values from domain D upon which constraints in set C are satisfied.
Constraint solving
oUse clever algorithms to solve a CSP problem
•Node, Arc & Path consistencies
•Constraint propagation

6. Constraint satisfaction problem (CSP) vs. Generate & Test
15 variables [V1,..,V15] all taking values in the domain {1,..,15}
V1<V2, V2<V3, …, V14<V15
Generate & Test Approach
Enumerating all possible assignments
1515= 437,893,890,380,859,375 possibility
109assignments/second computer would need 14 years to find solution

7. Constraint satisfaction problem (CSP) vs. Generate & Test
Model as a constraint satisfaction problem
Constraint satisfaction Solving
Interleaving generation and checking
After each choice check if constraints have been violated and then fail early
Propagate & distribute
Making tests active rather than passive
oNot just testing whether constraints are violated or not but making them active and propagate constraints
V1 < V2
oV2 must be 1 greater than V1
oV1 = {1,..15} and V2 = {2,..,15}
Repeat this reasoning until V14 < V15
oV15 = {15}

8. Combinatorial Design Problems using sets
Combinatorial Design Problems
Study of combinatorial design, which are collection of subsets with certain intersection properties
Approach
Model variables as sets
Solve using set solvers

9. Combinatorial Design Problems using sets
Ternary Steiner systems
Select 3-element subsets from the set {0,1,2,3,4,5,6} such that each object occurs in 3 of the subsets and the intersection of every two subsets has precisely one member.
Model
Use intersection constraint to state that the intersection of every two 3- element subsets has precisely one member
Use element constraint to state that each element occurs in 3 of the 3- element subsets
Solving
Set solver

10. Combinatorial Design Problems using sets
Ternary Steiner systems
Solving
Set solver
Order in sets doesn’t matter
Symmetry breaking
o{0,1,2}
o={1,0,2}
o={2,1,0}
o={0,2,1}
Solution
{012},{034},{056},{135},{146},{236},{245}

11. Combinatorial Problems as SAT problems
Boolean satisfaction problems (SAT)
The problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE.
Example
For (A B) (B ¬C) (A ¬B) to be true which variables have to be true to satisfy all clauses ?
Approaches
oExhaustive search in the form of truth table to find the solution
•Number of rows for the truth table is 2# of variables

12. Combinatorial Problems as SAT problems
Model as a SAT problem and use SAT solvers
SAT solvers
Davis-Putnam Algorithm
Splits the clauses using truth assignments
(A B) (B ¬C) (A ¬B) B (B ¬C) ¬B
B ¬C()
()¬C
 
() A=0
A=1B=0
B=1B=0
B=1C=0
C=1() = Failed Partial Assignment = Successful Partial Assignment

13. Error correcting & Cryptology
In a good cryptographic system, changing one bit in the cipher text changes enough bits in the corresponding plain text to make it unreadable.
What causes the change/error of the cipher text?
Noise from communication channels
Could be an attack

14. Error correcting & Cryptology
Holding a conversation in a noisy room becomes more difficult as the noise become louder.
Data transmission becomes difficult as the communication channel gets noisier.
Solution ?
Raise your voice
Repeat yourself
Adding some redundancy to the transmission in order for the recipient to be able to reconstruct the message.
Replace the symbols in the original message by codewords that have some redundancy built into them.
Code words
Block codes (not varying in length)

15. Hamming Distance Problem
We are trying to find how close the 2 codewords/code vectors are.
The Hamming Distance = d(u,v)
The number of places where the 2 codewords/code vectors differ.
Examples
u = (1,0,1,0,1,0,1,0)
v = (1,0,1,1,1,0,0,0)
d(u,v) = 2

16. Hamming distance optimization problem
As an optimization problem then, the task is to find (and prove) the maximum size (number of codewords = a(n, d,w)) for a binary error correcting code with given parameters (n, d) and optionally fixed weight (w).
Approach
Trying to find increasingly larger codes and proving optimality by failing to find one larger.

17. Hamming Distance Optimization problem
How to model this ?
Using set variables (Si) to represent code words (Ci)
The element x is in the set Si iffthe code Cihas a 1 at position x
[0000]->S={}
[1000]->S={1}
[0100]->S={2}
[1100]->S={1,2}

18. Hamming Distance Optimization problem
Example
a(4,1,1)
How many code words of length 4 , minimal distance of 1 and weight 1 ?
[1000]S = {1}
[0100]S = {2}
[0010]S = {3}
[0001]S = {4}
Answer = 4

19. Logical Cryptanalysis of DES
What is DES ?
Data encryption standard which is a state of the art cipher system used to encrypt/decrypt text.
Cryptanalysis
Trying to break the cipher system and acquire key
Logical cryptanalysis of DES ?
Modeling the DES algorithm as a SAT problem and therefore explicit representation of Plain bits, Key bits, and Cipher bits.

20. Logical Cryptanalysis of DES

21. Logical Cryptanalysis of DES

22. Logical Cryptanalysis of DES
ε(P,K,C)
which is true if and only if for the corresponding sequences of bits (P0,P1,C0,C1,… etc) we have that C = Ek(P) holds.

23. Logical Cryptanalysis
Now that we have modeled our problem
We can use the formula to crack the key given a known plain text and cipher text.
We can find out interesting properties of the cipher system
Faithful cipher
for any pair of plaintext and cipher text there is only one key that could have produced them.

24. Thank you